灰色马尔可夫理论建筑业碳排放量预测

在明确碳排放量计算公式和碳排放因子的基础上，文章建立建筑施工过程中碳排放量预测模型，并对建筑施工过程中材料及机械设备使用情况进行实证分析，得出建筑面积与施工过程碳排放量存在显著的线性关系。最后通过实例对该碳排放量预测模型进行应用研究。

应用灰色系统理论和马尔可夫链预测理论建立了纳米复合陶瓷刀具磨损量的灰色-马尔可夫链预测模型,研究了刀具磨损量和刀具寿命的预测方法。awt纳米复合陶瓷刀具的磨损量及刀具寿命预测结果表明,预测值与实测值误差较小。

交通量是一个不平稳的时间序列,在不确定性条件和缺乏数据资料的情况下,交通量的预测是一个较复杂的问题。灰色马尔科夫链模型是一种结合经典灰色理论和马尔科夫链的状态转移行为的预测模型。该模型在灰色预测理论的基础上,再对随机波动大的残差序列进行马尔科夫预测,实现了两者的优势互补,克服了两者的不足。以太原市漪汾桥断面的交通量的数据在传统灰色gm(1,1)预测模型的基础上建立交通量的灰色马尔科夫链模型,研究表明,该模型在交通量的预测方面相对传统的灰色gm(1,1)模型有更高的精度。

基于灰色理论和马尔科夫理论,建立传统的灰色预测模型和灰色马尔科夫预测模型,对西安地铁客流量的数据进行分析预测；然后对原始数据序列滑动平均处理,再用无偏gm(1,1)模型拟合系统的发展变化趋势,将修正后得到的模型与马尔科夫模型进行结合,提出改进的灰色马尔科夫模型预测方法。利用改进后的新模型对地铁客流的预测结果与传统的灰色马尔科夫模型进行对比。结果表明,改进后的灰色马尔科夫模型预测精度有显著提高。

本文将马尔柯夫理论与灰色理论相结合，建立了gm（（1，1）模型，并将其应用于实际．本文针对重庆市商品房价格进行了建模分析，并预测了未来价格的发展的趋势，相对于单用马尔柯夫理论建模提高了精度。

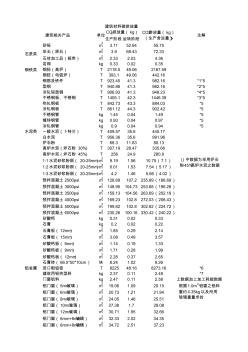
生产阶段运转阶段 砂砾m 3 3.1152.64 采石（原石）m33.968.43 石材加工品（板类）m22.332.03 岩棉kg0.330.02 钢胚（高炉）t2118.549.06 钢胚（电弧炉）t393.149.06 钢筋及铁件t923.4541.3 型钢t940.8641.3 冷轧轻型钢t906.9341.3 不锈钢板、不锈钢t1405.142.3 热轧钢板t842.7343.3 冷轧钢板t861.1244.3 不锈钢管kg1.450.04 镀锌钢管kg0.930.04 冷轧钢管kg0.90.04 一般水泥（卜特兰）t409.5735.6 白水泥t956.3635.6 炉石粉t68.311.83 高炉水泥（炉石粉30%）t307.1928.47 高炉水泥（炉石粉45

基坑预测问题关系到工程施工的安全,在施工过程中对基坑进行周密的监测和变性预测分析显得尤为重要.针对传统预测模型存在固有偏差和可靠性低的缺点,采用新陈代谢的原理对无偏灰色加权马尔科夫模型进行改进.该模型先用无偏灰色模型拟合系统的总体变化趋势,然后,对拟合残差进行马尔可夫状态划分,并根据各阶权重对不同步长的转移矩阵进行加权处理,用加权后的无偏灰色马尔科夫模型进行预测.在每一步的预测中,利用新陈代谢的原理不断更新建模所使用的数据.将该模型用于基坑沉降预测,并通过实例进行验证.实验表明:基于新陈代谢的无偏灰色加权马尔科夫模型提高了基坑沉降预测的精度和可靠性,预测精度与未改进模型相比提高了8.54%.

我国建筑事故预测中具有统计数据少、数据波动性大等特点,缺乏具有高精度、可操作性强的预测模型。将灰色系统理论和马尔可夫原理相结合,充分发挥了灰色系统理论适用于小样本数据拟合和马尔可夫适合处理数据波动大的系统过程的优势,通过gm(1,1)模型的建立,提出一种适合建筑事故统计数据特点的灰色马尔可夫预测方法。将该方法应用于1994—2007年建筑施工事故次数分析,以此为基础对2008—2009年的建筑施工事故次数进行预测。研究结果表明:基于灰色马尔可夫理论建筑事故预测结果精度可达90%以上。

建筑物作为一个特殊的物体,必须正确预测其变形发展趋势,灰色gm(1,1)模型由于自身的局限性使其在沉降预测中显得方法单一。本文提出一种预测模型,灰色马尔可夫模型,该模型结合了灰色模型和马尔可夫模型的优点,共同来判断建筑物的发展趋势,并通过实例来验证该方法的可行性。

以低碳为特征的绿色建筑技术是解决我国资源和环境瓶颈以及应对气候变化的关键举措。本文以控制住宅建筑的碳排放量、发展低碳绿色建筑为目标,从建材的生产、运输、建筑施工、正常使用、拆除以及拆除以后废弃物的处理等方面,对住宅建筑的能源消耗、co2排放量及节能减排的措施和潜力进行了分析,归纳了建筑能耗的类别并对其进行了分析。分析结果表明,住宅建筑在使用阶段和建材生产阶段的能耗和碳排放量占建筑总能耗和总碳排放量的90%以上,而且这2个阶段的能耗和碳排放量均具有较大的节能减排潜力;其它3个阶段的能耗和碳排放量相对很小。

结合灰色理论短期预测优势以及马尔科夫预测模型无后效性特点,建立基于灰色-马尔科夫理论的组合预测模型,研究沥青路面性能衰变规律。以重庆某高速公路历年rqi检测数据为例,用matlab计算rqi灰色预测值并验证模型的精度；通过灰色预测方程反算使用年限序列,并建立马尔科夫状态转移矩阵,对rqi进行预测。结果表明:灰色预测模型对rqi预测精度达到一级,预测结果可靠性较高；根据灰色-马尔科夫模型,预测rqi衰变规律,对比单一的灰色预测模型,灰色-马尔科夫组合预测模型精度更高,更适用于路面性能的长期预测。

针对随机波动较大的施工质量成本预测问题,结合灰色scgm(1,1)预测模型和马尔可夫预测模型的优点,建立了灰色马尔可夫scgm(1,1)预测模型,并以实例证明灰色马尔可夫预测模型对随机波动性较大的施工质量成本的数据列的预测,具有较高的准确性。

将结合灰色系统理论与马尔可夫理论,对公路交通事故进行预测.利用灰色马尔可夫预测模型,可有效地处理类似交通事故等随机性、波动较大的数据。

针对公路运量预测中弹性系数随机波动性较大的问题,结合灰色模型可以揭示预测数据的发展趋势以及马尔可夫预测适合描述随机波动性较大的预测问题的优点,建立了公路运量预测中弹性系数的灰色马尔可夫预测模型;用该模型对北京市公路客运弹性系数进行预测,验证了模型对公路运量中弹性系数进行预测的合理性。研究结果表明,灰色马尔可夫预测模型能够较好地提高公路运量预测中弹性系数的预测精度,对于提高公路运量预测精度具有重要意义。

灰色模型不适合长期、随机性和波动性较大的数据序列预测,针对这一问题引入马尔可夫预测理论,建立了公路运输弹性系数的灰色马尔可夫预测模型。模型兼有灰色预测和马尔可夫预测的优点,克服了随机波动性数据对公路运输弹性系数预测精度的影响,拓宽了灰色预测模型的应用范围。通过湖南省公路客运弹性系数预测的实例证明,基于灰色马尔可夫的公路运输弹性系数预测模型的预测精度普遍高于灰色gm(1,1)模型的预测精度,具有较好的实用性。

灰色模型是经济预测方法中最有效的方法之一,但灰色模型对波动性大的序列预测时精度较差。针对这一不足,提出灰色-马尔可夫的改进模型。新模型将原始序列进行对数运算提高数据光滑度,采用距离法降低灰色模型的相对误差,马尔可夫链对预测值进一步修正。将改进模型运用到景德镇陶瓷工业产值预测中,并与传统灰色模型、灰色-马尔可夫模型预测结果进行对比。结果表明改进模型的相对误差远小于灰色模型,预测精度优于灰色-马尔可夫模型,更能反应经济发展趋势。

科学的货运量预测对铁路发展战略的制定具有十分重要的意义.针对灰色模型的预测结果精确度受原始数据变化幅度的影响较大,且要求累加生成的数据列具有指数性质的缺点,采用带波动的多项式来替代gm(1,1)模型中的指数形曲线,并通过马尔可夫链对其预测结果进行修正,从而建立改进的灰色-马尔可夫链预测模型,同时利用该改进模型对我国铁路货运量进行预测,并与传统的gm(1,1)模型、改进的gm(1,1)模型和灰色-马尔可夫模型3种预测方法进行了比较,结果表明:提出的预测方法具有较高的精度,具有一定的可行性和有效性,预测结果可指导铁路建设与管理.

根据公路桥梁荷载的特点,采用新维改进灰色马尔科夫模型进行公路桥梁荷载预测。通过实例预测结果和实测结果比较可知,应用该预测模型对桥梁荷载进行预测,其预测精度、准确度较高,本荷载预测模型可以直接应用于桥梁结构设计和耐久性研究。

以建筑施工过程中频发的坍塌事故为研究对象,将灰色gm(1,1)模型与马尔柯夫预测技术相结合,构建坍塌事故的灰色马尔柯夫预测模型,并以我国三级以上建筑工程坍塌事故统计数据为基础,对我国坍塌事故进行趋势分析和状态预测。

城市污水及主要污染物排放量的灰色预测模型

桥梁耐久性预测不仅可以揭示桥梁在整个使用期间耐久性退化过程和变化趋势,而且是采取合理维修加固方案的依据。该文考虑桥梁耐久性检测数据非等时距的特点,采用三弯矩法对其进行处理,并在处理数据基础上,应用灰色-马尔科夫组合模型进行模拟,并提出组合模型对桥梁耐久性进行预测,解决了传统模型无法考虑不确定因素和耐久性状况不平稳变化的影响。最后通过对辽宁省某桥的耐久性进行实际预测,并将计算结果进行对比,验证了改进模型的有效性和实践性。

将铁路客运量预测分为运量趋势预测和运量波动预测,分别采用灰色gm(1,1)模型和马尔柯夫过程进行预测,并将两者结合形成灰色马尔柯夫铁路客运量预测方法。根据1990年—2002年的铁路客运量数据,预测2003年的客运量以检验模型预测效果,并对我国“十一五”期间铁路客运量进行预测,分析证明基于灰色马尔柯夫过程预测方法的预测可信度。