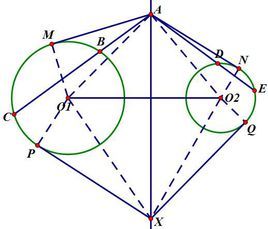
若PM⊥AB,则有AP ^2一AM^2 =BP^2 一BM^2。
证明:若直线PM⊥AB于N,则
AP^2 一AN^2 = PN^2;
AM^2 一AN^2 = MN^2.
以上两式相减得
AP^2 一AM^2 = PN^2 一MN^2.①
同理,
BP^2 一BM^2 = PN^2 一MN^2.②
由式①、②得
AP^2 一AM^2 = BP^2 一BM^2 .③
证毕。
反之,若有AP ^2一AM^2 =BP^2 一BM^2成立,则PM⊥AB。
证明:设∠ANP=α,则∠BNP=π-α.
故AP^2 一AM^2
= AN^2 + PN^2 - 2AN·PNcosα+2AN·MNcosα一AN^2 一MN^2
= PN^2 一MN^2 一2AN·PNcosα+2AN·MNcosα.
BP^2 一BM^2
= PN^2 + BN^2 一2PN·BNcos(π-α) 一MN^2 一BN^2 + 2MN·BNcos(π-α).
= PN^2 一MN^2 + 2PN·BNcosα一2MN·BNcosα.
由式③得
2AN·MNcosα一2AN·PNcosα
= 2PN·BNcosα一2MN·BNcosα,
即MN(AN + BN)cosα
= PN(AN + BN)cosα.
从而,(PN 一MN) cosα=0,即PM cosα=0.
因此,cosα=0.
又因为0<α<π,所以α= π/2.
故PM⊥AB.
证明:以长度为d的线段AB上任意一点为原点O,过O点且垂直于线段AB的直线OM为y轴建立以OA为x正半轴的平面直角坐标系,并设A(一t,0)、B(d-t,0)、M(x,y),(其中t>0),则
∵AM^2 一MB^2=k(定值)
∴[(x+t)^2-y^2]- [(x-d+t)^2-y^2]=k
∴x=﹙d^2-2dt+k﹚/d(常数)
所以,点M的轨迹是一条垂直于AB的直线。