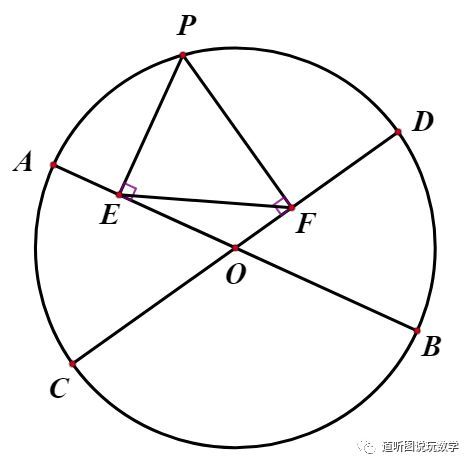
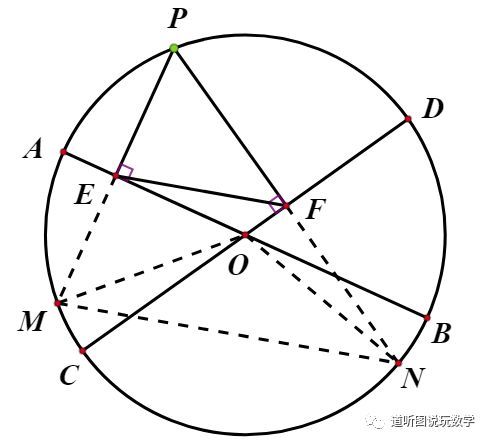
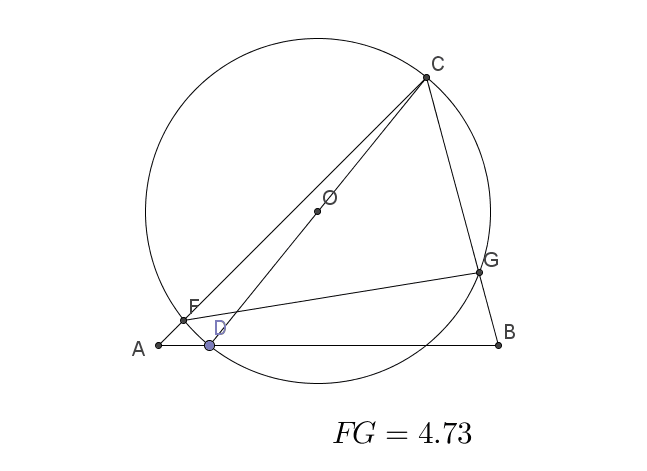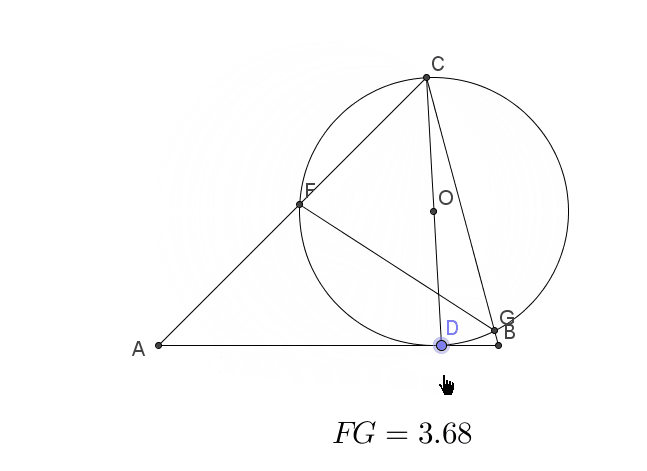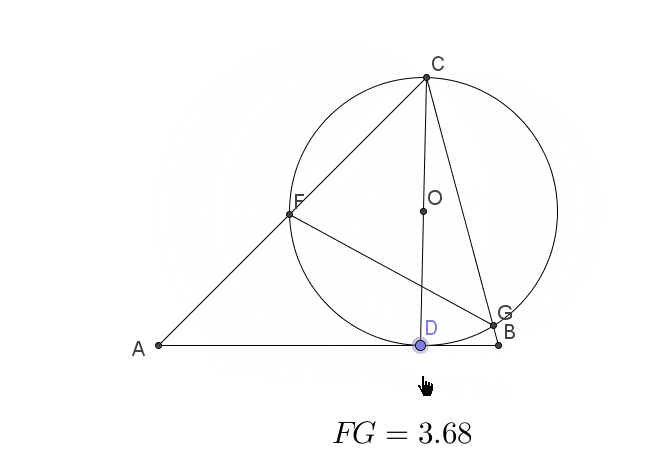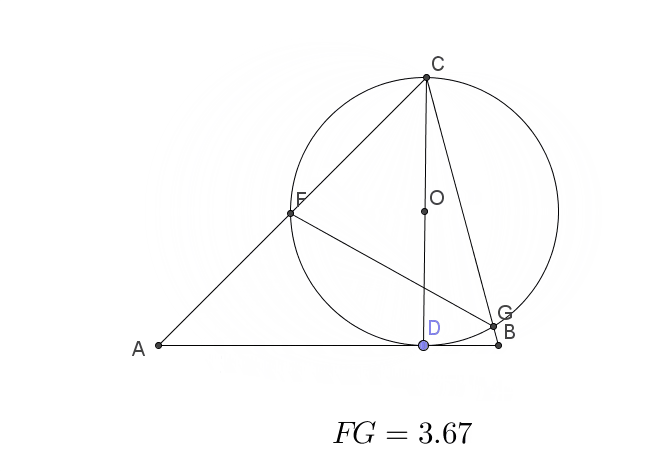
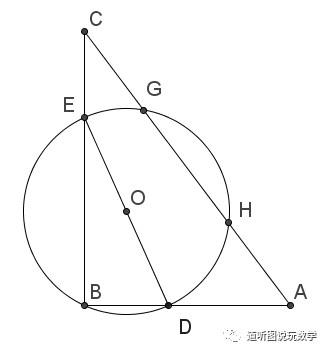
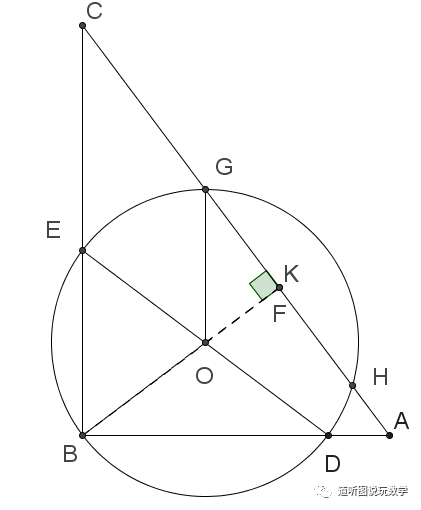
动点问题之三点共线求线段最值文献

 不共线三点确定二次函数的表达式优质课教学设计
不共线三点确定二次函数的表达式优质课教学设计
不共线三点确定二次函数的表达式优质课教学设计
1 / 3 不共线三点确定二次函数的表达式 【教学目标】 (一)知识与技能: 1.掌握用待定系数法列方程组求二次函数解析式。 2.由已知条件的特点,灵活选择二次函数的三种形式,合适地设置函数解析式,可使计 算过程简便。 (二)过程与方法: 通过例题讲解使学生初步掌握,用待定系数法求二次函数的解析式。 (三)情感态度: 通过本节教学,激发学生探究问题,解决问题的能力。 【教学重点】 用待定系数法求二次函数的解析式。 【教学难点】 灵活选择合适的表达式设法。 【教学过程】 一、情境导入,初步认识: 1.同学们想一想,已知一次函数图像上两个点的坐标, 如何用待定系数法求它的解析式? 2.已知二次函数图像上有两个点的坐标,能求出其解析式吗?三个点的坐标呢? 二、思考探究,获取新知: 探究 1:已知三点求二次函数解析式讲解: 让学生通过课本例 1、例 2,讲解归纳出已知三点坐标求二次函数解析式的方法

 线管配线工程煨弯采用二点二线法和三点三线法施工的优点
线管配线工程煨弯采用二点二线法和三点三线法施工的优点
线管配线工程煨弯采用二点二线法和三点三线法施工的优点
电气施工中常采用(YB242-63)电焊钢管,(YB-234-63)水、煤气管和(HG2-63-65)硬聚氯乙烯管作为明敷或暗敷的线管,进行配线施工。在施工中有大量需要煨弯的管段。现场常用的方法是以米尺在管子上量好尺寸,并留出煨弯时的伸缩量,在管子上做上标记,然后煨弯。但经常出现图1和图2所示的现象。