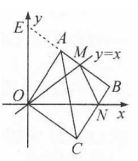
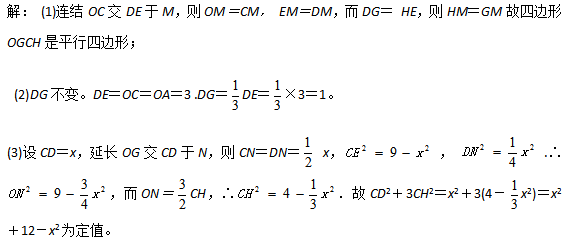几何尺规作图问题文献

 几何变换思想
几何变换思想
几何变换思想
几何变换思想 变换是数学中一个带有普遍性的概念, 代数中有数与式的恒等变换、 几何中 有图形的变换。 在初等几何中, 图形变换是一种重要的思想方法, 它以运动变化 的观点来处理孤立静止的几何问题, 往往在解决问题的过程中能够收到意想不到 的效果。 1. 初等几何变换的概念。 初等几何变换是关于平面图形在同一个平面内的变换, 在中小学教材中出现 的相似变换、合同变换等都属于初等几何变换。合同变换实际上就是相似比为 1 的相似变换,是特殊的相似变换。合同变换也叫保距变换,分为平移、旋转和反 射 (轴对称 )变换等。 (1) 平移变换。 将平面上任一点 P变换到 P′,使得: (1) 射线 PP′的方向一定; (2) 线段 PP′的长度一定,则称这种变换为平移变换。也就是说一个图形与经 过平移变换后的图形上的任意一对对应点的连线相互平行且相等。 平移变换有以下一些性质: ①把图形变为与之全等的图

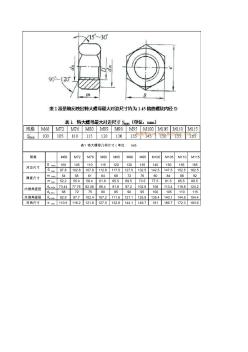 特大螺母几何尺寸
特大螺母几何尺寸
特大螺母几何尺寸
规格 M68 M72 M76 M80 M85 M90 M95 M100 M105 M110 M115 S max 100 105 110 115 120 130 135 145 150 155 165 S min 97.8 102.8 107.8 112.8 117.5 127.5 132.5 142.5 147.5 152.5 162.5 m max 54 58 61 64 68 72 76 80 84 88 92 m min 52.2 55.4 58.4 61.8 65.5 69.5 73.5 77.5 81.5 85.5 89.5 da max 73.44 77.76 82.08 86.4 91.8 97.2 102.6 108 113.4 118.8 124.2 da min 68 72 75 80 85 90 95 100 105 110 115 外倒角直径 dw min 92.