选择特殊符号

Ф δ ° × # Ⅱ Ⅲ ½ ¼

选择搜索类型

市场价信息价参考价询价供应商云知资讯文库百科

热门搜索

造价通

请输入搜索

首页 > 百科 > 建设工程百科

截面抵抗矩

截面抵抗矩（W）就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值。 工程实际中最常见的弯曲问题是横力弯曲，横截面上不仅有正应力，而且还有切应力。由于切应力的作用，横截面发生翘曲，平面假设不再成立。但进一步的理论分析证明，对于跨长与截面高度比 l/h>5 的长梁利用公式δ=My/I 来计算其横力弯曲的正应力，所得结果误差甚微，足够满足工程实际需要。其中W=I/y，W称为抗弯截面系数。 由于横力弯曲时，梁的弯矩随截面位置变化，Mmax所在截面称为危险截面，最大弯曲正应力发生在弯矩最大的截面上，且离中心轴最远处，该处为危险点。

截面抵抗矩基本信息

中文名截面抵抗矩
外文名Sectional resistance moment
作用计算弯矩作用下截面最外边正应力
主要领域工程设计等
简称W

截面抵抗矩不同公式

矩形截面抵抗矩： （其中b为垂直于弯矩作用方向的长度）。 圆形截面的抵抗矩：抗弯时 （其中d为直径），抗扭时 。 圆环截面抵抗矩：抗弯时 ，抗扭时 。2100433B

截面抵抗矩造价信息

市场价
信息价
询价

小截面塑力电缆

规格型号：
ZR-YJV22 4×6型号:ZR-YJV22;标称截面(mm2):6;芯数:4;额定电压:0.6/1KV;
价格行情：
材料单位：
m
材料品牌：
辽缆
材料税率：
13%
供应商：
沈阳辽缆电线电缆制造有限公司
报价时间：
2022-12-07

查看价格

YJV铜芯高压交联聚乙烯绝缘标称截面（平米）：185

规格型号：
三芯6/6kv;
价格行情：
材料单位：
卷
材料品牌：
峰岩
材料税率：
13%
供应商：
新疆峰岩线缆有限公司
报价时间：
2022-12-07

查看价格

YJLV铜芯高压交联聚乙烯绝缘标称截面（平米）：50

规格型号：
6/6kv;
价格行情：
材料单位：
卷
材料品牌：
峰岩
材料税率：
13%
供应商：
新疆峰岩线缆有限公司
报价时间：
2022-12-07

查看价格

YJV铜芯高压交联聚乙烯绝缘标称截面（平米）：25

规格型号：
三芯6/6kv;
价格行情：
材料单位：
卷
材料品牌：
峰岩
材料税率：
13%
供应商：
新疆峰岩线缆有限公司
报价时间：
2022-12-07

查看价格

远东牌FZD0.6/KV系列预制分支电缆(标称截面:1*240mm2)

规格型号：
NH-VV
价格行情：
材料单位：
km
材料品牌：
材料税率：
13%
供应商：
江苏新远东电缆有限公司柳州业务部
报价时间：
2022-12-07

查看价格

自升式塔式起重机

规格型号：
起重量矩1500kNm
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2007年4季度信息价
所属行业：
建筑工程
备注说明：

查看价格

自升式塔式起重机

规格型号：
起重量矩2000kNm
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2007年4季度信息价
所属行业：
建筑工程
备注说明：

查看价格

自升式塔式起重机

规格型号：
起重量矩1000kNm
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2007年3季度信息价
所属行业：
建筑工程
备注说明：

查看价格

自升式塔式起重机

规格型号：
起重量矩1500kNm
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2007年3季度信息价
所属行业：
建筑工程
备注说明：

查看价格

自升式塔式起重机

规格型号：
起重量矩2000kNm
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2007年3季度信息价
所属行业：
建筑工程
备注说明：

查看价格

火矩花

规格型号：
火矩花,H90-100,P45-50
需求量：
5000株
报价数：
3
材料品牌：
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2019-11-26

查看价格

数字矩陈

规格型号：
定制
需求量：
0套
报价数：
1
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2010-05-05

查看价格

细叶萼矩花

规格型号：
高度(m) 0.2-0.25 ,冠幅(m)0.15-0.2
需求量：
36.42m²
报价数：
3
材料品牌：
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2022-05-07

查看价格

矩钢管

规格型号：
80×40×3
需求量：
85.144m
报价数：
3
材料品牌：
材料档次：
中高档
费用说明：
含税费 | 含运费
询价时间：
2021-04-26

查看价格

矩钢管

规格型号：
50×30×2
需求量：
115.065m
报价数：
3
材料品牌：
材料档次：
中高档
费用说明：
含税费 | 含运费
询价时间：
2021-04-26

查看价格

截面抵抗矩作法

1）找出达到极限弯矩时截面的中和轴。 中和轴分为弹性中和轴和塑性中和轴； 弹性状态下的中和轴：整个截面关于经此轴线的截面面积矩为0。横截面在此轴线弯曲正应力为0。 截面面积矩：指弹性状态下截面各微元面积与各微元至中和轴距离乘积的积分。单位mm。指弹性状态下中和轴一侧截面的面积矩，主要用于计算截面上任意点的剪切应力值。 塑性状态下的中和轴：塑性中和轴为构件截面面积平分线，该中和轴两边的面积相等。 2） 弹性状态下截面抵抗矩：如本文开头定义。其意义在于在弹性状态下计算某一构件断面位置最不利位置的最大应力，该位置应力满足则此位置截面满足计算要求； 塑性状态下截面塑性抵抗矩：分别求两侧面积对中和轴的面积矩，面积矩之和即为塑性截面模量，也称为塑性抵抗矩。

截面抵抗矩常见问题

截面抵抗矩的介绍

截面抵抗矩（W）就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值。工程实际中最常见的弯曲问题是横力弯曲，横截面上不仅有正应力，而且还有切应力。由于切应力的作用，横截面发生翘曲，平面假设不再成立...
什么是截面抵抗矩?

截面抵抗矩就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值。工程实际中最常见的弯曲问题是横力弯曲，横截面上不仅有正应力，而且还有切应力。由于切应力的作用，横截面发生翘曲，平面假设不再成立。但...
什么是截面抵抗矩，怎么算

截面抵抗矩：一种是塑性截面抵抗矩(塑性设计时采用),一种是弹性截面抵抗矩(弹性设计时采用)。截面抵抗矩是截面本身所具有的特性，与外力无关，所以要用W=2Ix/h计算，当然这个公式也只是适用于对...

截面抵抗矩文献

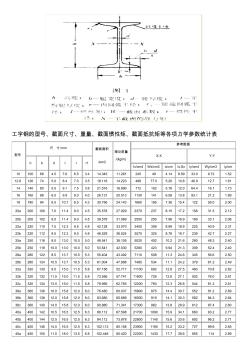工字钢和槽钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表

工字钢和槽钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表

工字钢和槽钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表

格式：pdf

大小：236KB

页数： 3页

工字钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表型号尺寸 /mm 截面面积 /em2 理论质量 /(kg/m) 参考数值 X-X Y-Y h b d t r r1 1x/cm4 Wx/cm3 ix/cm Ix:Sx Iy/cm4 Wy/cm3 iy/cm 10 100 68 4.5 7.6 6.5 3.4 14.345 11.261 245 49 4.14 8.59 33.0 9.72 1.52 12.6 126 74 5.0 8.4 7.0 3.5 18.118 14.223 488 77.5 5.20 10.8 46.9 12.7 1.61 14 140 80 5.5 9.1 7.5 3.8 21.516 16.890 712 102 5.76 12.0 64.4 16.1 1.73 16 160 88 6.0 9.9 8.0 4.0 26

在线阅读立即下载

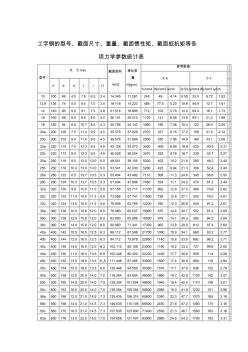工字钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表

工字钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表

工字钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表

格式：pdf

大小：236KB

页数： 2页

工字钢的型号、截面尺寸、重量、截面惯性矩、截面抵抗矩等各项力学参数统计表型号尺寸 /mm 截面面积 /em2 理论质量 /(kg/m) 参考数值 X-X Y-Y h b d t r r1 1x/cm4 Wx/cm3 ix/cm Ix:Sx Iy/cm4 Wy/cm3 iy/cm 10 100 68 4.5 7.6 6.5 3.4 14.345 11.261 245 49 4.14 8.59 33.0 9.72 1.52 12.6 126 74 5.0 8.4 7.0 3.5 18.118 14.223 488 77.5 5.20 10.8 46.9 12.7 1.61 14 140 80 5.5 9.1 7.5 3.8 21.516 16.890 712 102 5.76 12.0 64.4 16.1 1.73 16 160 88 6.0 9.9 8.0 4.

在线阅读立即下载

塑性截面抵抗矩简介

截面塑性抵抗矩Wpx。 1）找出达到极限弯矩时截面的中和轴。它是与弯矩主轴平行的截面面积平分线，该中和轴两边的面积相等。在双轴对称截面中，这条轴是主轴。 2）分别求两侧面积对中和轴的面积矩，面积矩之和即为塑性截面模量。2100433B

截面模量不同公式

矩形截面抵抗矩： （其中b为与弯矩垂直方向的长度）。 圆形截面的抵抗矩：抗弯时 （其中d为直径），抗扭时 。 圆环截面抵抗矩：抗弯时 ，抗扭时 。 2100433B

截面模量概述

截面模量又叫截面抵抗矩。被弯曲构件的横截面绕其中性轴的惯性矩除以由中性轴到截面最外边缘的距离。（单轴对称时，有一个最大截面模量和一个最小截面模量。）可以用来计算截面受弯时的正应力大小。 截面抵抗矩（W）就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值。 工程实际中最常见的弯曲问题是横力弯曲，横截面上不仅有正应力，而且还有切应力。由于切应力的作用，横截面发生翘曲，平面假设不再成立。但进一步的理论分析证明，对于跨长与截面高度比 l/h>5 的长梁利用公式δ=My/I 来计算其横力弯曲的正应力，所得结果误差甚微，足够满足工程实际需要。其中W=I/y，W称为抗弯截面系数。 由于横力弯曲时，梁的弯矩随截面位置变化，Mmax所在截面称为危险截面，最大弯曲正应力发生在弯矩最大的截面上，且离中心轴最远处，该处为危险点。

相关推荐

相关百科
相关知识
相关专栏

免费服务热线: 400-888-9639