几何体
由平面和曲面所围成。一般来说一个几何体是由面、交线、而构成的。
-

选择特殊符号
选择搜索类型
请输入搜索
由平面和曲面所围成。一般来说一个几何体是由面、交线、而构成的。

你好!很高兴为你解答,有在网上帮你查阅相关资料请你参考:花盆的种类很多,就列举个比较常见的花盆几何体吧!圆台因上下粗细同差多啦初单元应该还没学圆台
石膏几何体有不同的分类,所以价格也是不一样的,被用来当画画的模板来使用的价格不是很高,每个售价在50元左右,如果是石膏几何体的装饰品,价格稍微高一点,每个售价在150元左右。以上价格来源于网络,仅供参...
不是,有的垂直有的不垂直。。。。

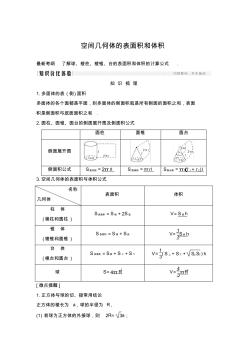 空间几何体的表面积和体积
空间几何体的表面积和体积
空间几何体的表面积和体积
空间几何体的表面积和体积 最新考纲 了解球、棱柱、棱锥、台的表面积和体积的计算公式 . 知 识 梳 理 1.多面体的表 (侧)面积 多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面 积是侧面积与底面面积之和 . 2.圆柱、圆锥、圆台的侧面展开图及侧面积公式 圆柱 圆锥 圆台 侧面展开图 侧面积公式 S圆柱侧=2π rl S 圆锥侧=π rl S圆台侧=π(r 1+ r 2) l 3.空间几何体的表面积与体积公式 名称 几何体 表面积 体积 柱 体 (棱柱和圆柱 ) S表面积=S 侧+2S 底 V=S 底h 锥 体 (棱锥和圆锥 ) S 表面积=S 侧+S底 V= 1 3S底 h 台 体 (棱台和圆台 ) S 表面积=S侧+S 上+S 下 V= 1 3( S 上+S下+ S上S下) h 球 S=4π R 2 V= 4 3πR 3 [微点提醒 ] 1.正方体与球的切、

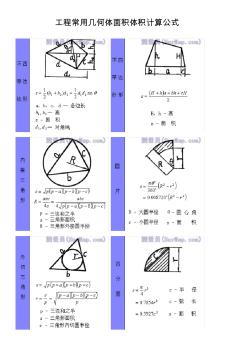 工程常用几何体面积体积计算公式
工程常用几何体面积体积计算公式
工程常用几何体面积体积计算公式
工程常用几何体面积体积计算公式 放坡公式 若 A B 为二边; H 为深度 1、一边放坡 V =A*B*H+1/2*K*H2〔A或 B〕 2、相邻二边坡 V=A*B*H+1/2*K* H2*[A+B]+1/3*K2H3 3、相对二边放坡 V=A*B*H+K* H2*[A 或 B] 4、三边放坡 V=A*B*H+1/2*K*H2*[(2A+B) 或 (2B+A)]+2/3* K2H3 5.四边放坡 V=(A+KH)*(B+KH)*H+1/3* K2H3 6.不放坡 V=ABH 其中三边放坡的体积比同样尺寸的四边放坡的体积要大要大很多,请问上面的公式正确吗? 从表面上看你的公式没有什么错误的,我也用数字导进去了,四边放坡的面积就是比三边放坡的面积大的,你是不是 了

前段时间在高三教学中遇到这样的问题:
在高考立体几何考点中涉及到空间几何体的截面的地方较多, 如:判断截面的形状、计算出空间几何体的截面周长或面积、或者求与之相关的体积问题、以及最值问题都在考察之列,但是要顺利地解决前面所提到的诸多问题,都必须首先掌握空间几何体截面的作图。
在立体几何中,把空间问题转化为平面问题,历来是立体几何的一个基本问题。而已知不共线三点,作几何体的截面,既是转化为平面问题的一个方法,也是深化理解空间点线面关系的一个很好的途径。
作几何体的截面,是立休几何教学中的一个难点,需要较强的空间想象能力和动手操作能力,正确判断几何体被一个平面所截的截面形状,关键在于弄清这个平面与几何体的面相交成线的形状和位置。让学生掌握作几伺体截面的方法,有助于深入理解直线和平面的有关性质,有效地形成空间概念。
一个平面截一个几何体,这个平面和几伺体的各个面交线,围成一个封闭的平面图形,这个封闭图形就称为几何体的截面。如果几何体是多面体,其截面是多面形;如果几何体是旋转体,其截面还可能是二次曲线所围成的封闭图形。
截面的问题的研究,对于发展学生的空间想象能力,综合运用立体几何各方面的知识技能,提高学生的解题能力,都是十分有启发、思考价值的题材、是立体几何重要的学习目的;而对学生进行空间几何体截面的作图等训练正是培养和发展学生的这一能力,同时也成为了促进学生综合运用空间构图方面知识开发教学兴趣点的拓展课题。
接下来小编从原理和操作两个层面介绍较复杂的不平行于底面的截面问题的解决方案以供参考。
空间几何体的截面的作图主要原理:两个公理及两个性质。
其中,两个公理为:
(1)如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线;
(2)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
两个性质为:
(1)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行;
(2)如果两个平面平行,第三个平面和它们相交,那么两条交线平行。
空间几何体的计算要掌握好“定位”、“定形”、“定量”这三个主要的环节。首先,由上面所讲到的方法确定出关键点。其次,由关键点确定截面与空间几何体相关的交线。再次,是根据问题中已知的条件与空间点、线、面的位置关系确定截面的基本特征。最后,运用平面解析几何的有关性质定理与判定定理完成截面相关截面边长、周长、或者面积等数量计算。
空间几何体的截面作图主要的作法:直接法、平行线法、延长法、辅助平面法,接下来,我们依次展开。
一、直接法

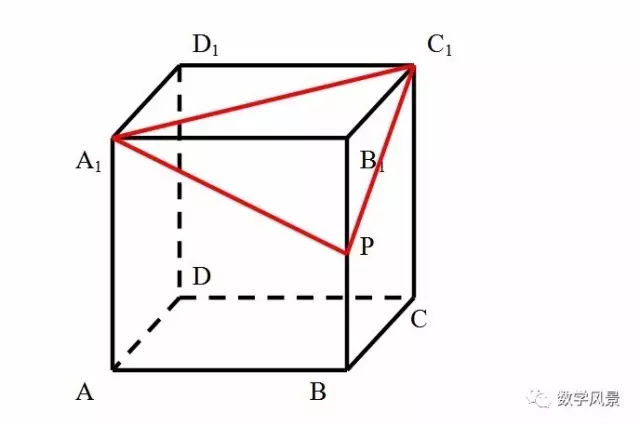
用直接法解决截面问题的关键是:截面上的点在几何体的棱上,且两两在一个平面内,我们可以借助于公理:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内,直接解决这类问题。
二、平行线法

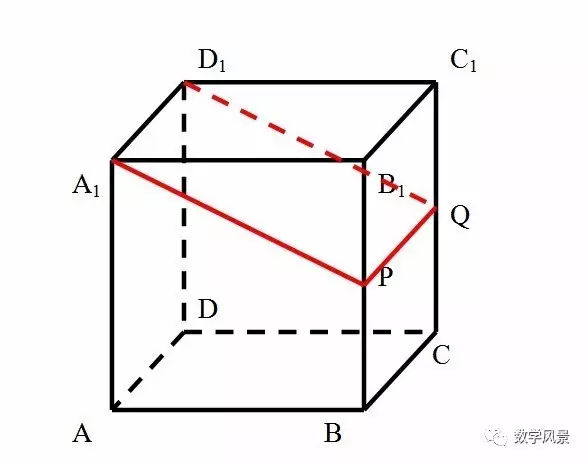
用平行线法解决截面问题的关键是:截面与几何体的两个平行平面相交,或者截面上有一条直线与截面上某点在几何体的某一个表面平行。我们可以借助于两个性质,(1)如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行;(2)如果两个平面平行,第三个平面和它们相交,那么两条交线平行。直接解决这类问题。
三、延长线法

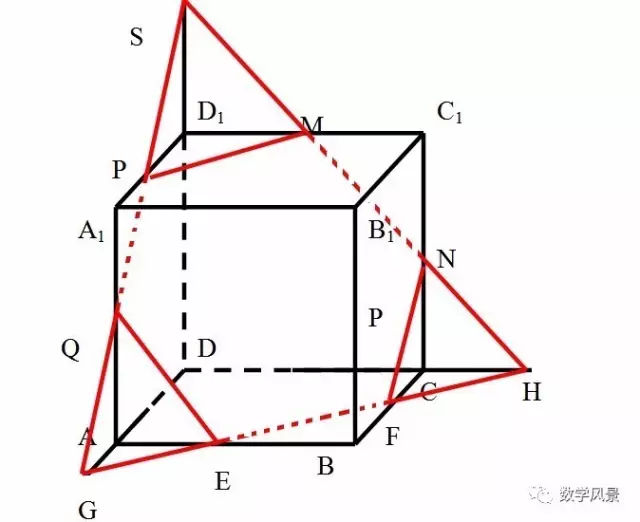
用延长线法解决截面问题的关键是:截面上的点中至少有两个点在一个几何体的一个表面上,我们可以借助于公理,如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。直接解决这类问题。
四、辅助平面法
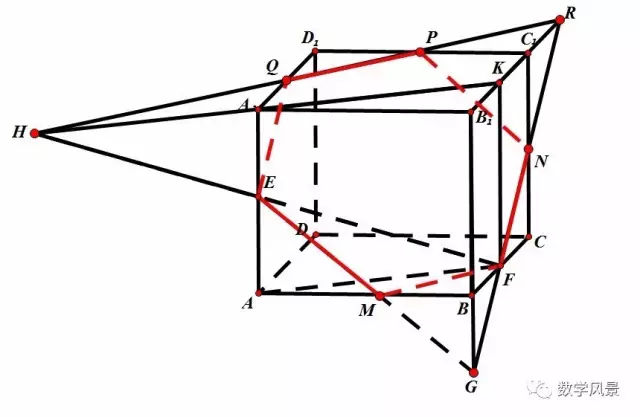

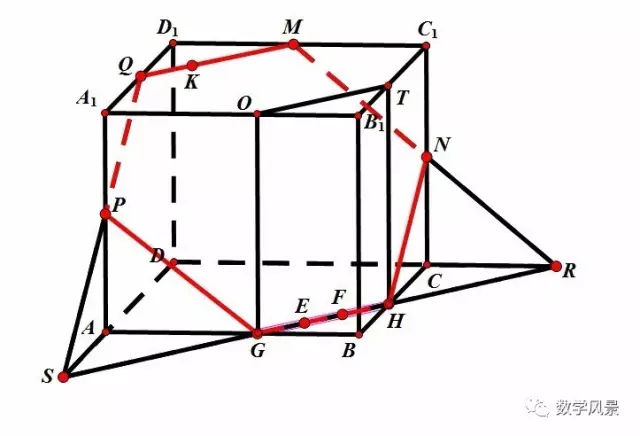

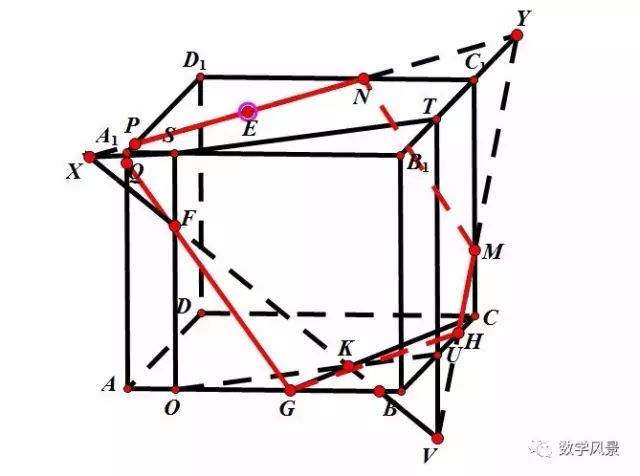

本节课通过创设图片问题情境,引入课题,通过多媒体动态展示学习三视图的概念,重点规范三视图的作图原则,大小:正俯等长,正侧等高, 侧俯等宽,位置:侧在正之右,俯在正之下.规范作图,通过辨析找出错误之处加深对作图的原则的理解和掌握,通过对比思考,掌握作图的注意事项:眼见为实,不见为虚,最后动手完成作几何体的三视图,提升能,总之本节课的中心就是掌握三视图的概念和作图
1. 投影仪呈现网络照片,学生猜想图中关系,和奥迪汽车设计图,增加趣味性,提高学习的兴趣,引出课题 2. 进行一个活动,作出三视图,标出三视图的长宽高及其关系 设置一个情景,通过多媒体动态展示正、侧、俯视图,从而得到三视图的相关概念 3. 学习掌握三视图的作图原则: 大小:正俯等长,正侧等高, 侧俯等宽 位置:侧在正之右,俯在正之下. 4. 从三视图当中找出错误,并更正,规范作图,并完成思考题加以巩固提高 5. 完成同一几何体— --圆台两种不同摆放时作三视图要注意的事项:眼见为实,看不见为虚的原则 6,独立完成立体,准确画出几何体的三视图 7,最好小结本节课所学习的内容 2100433B