单向应力状态的屈服条件由屈服极限（又称屈服应力，见材料的力学性能）表示，可由实验定出。对于屈服不明显的材料，在工程中将残余应变为0.2%的应力值定义为条件屈服极限σ_0.2，或把拉伸曲线（图1）中割线模量EY=0.7E处的应力作为条件屈服极限σ_Y，其中E为弹性模量。这种定义方法比测定残余应变量更简便。对于一般钢材，σ_0.2和σ_Y很

接近。某些金属材料在外力作用下产生塑性变形，卸载后再加载，屈服应力会有所提高，这种现象称为材料的强化现象。提高后的屈服应力称为后继屈服应力或加载应力。复杂应力状态下的情形有所不同。

为了描述材料在复杂应力状态下开始发生破坏时的受力程度，需要引入应力空间的概念，它是以应力分量为坐标的空间，在此空间中，每个点都代表一个应力状态，应力的变化在相应的空间中给出一条曲线，称为应力路径。根据不同的应力路径所进行的实验，可以定出从弹性阶段进入塑性阶段的各个屈服应力。在应力空间中将这些屈服应力点连起来，就形成一个区分弹性区和塑性区的分界面，这个分界面称为屈服面。描述屈服面的数学表达式就是屈服条件，它对应于单向应力状态下的屈服极限。同单向应力状态一样，在经历塑性变形后，低碳钢等材料的屈服极限没有什么变化，而强化材料的后继屈服应力比初始屈服应力有所提高。这些后继屈服点连成的面称为后继屈服面或加载面。初始屈服面转为后继屈服面的变化规律称为强化规律。

材料的初始屈服条件一般可表示为f(σ_ij)=C，其中σ_ij为应力分量；C为材料常数，可以通过实验测定。对于各向同性材料，屈服条件可用三个主应力 σ₁、σ₂、σ₃表示。这样，屈服条件可简化为f(σ₁，σ₂，σ₃)=C。在以主应力为坐标轴的主应力空间中，同对应的屈服面将空间分为两部分：包含原点的屈服面内的部分对应弹性状态（或刚性状态）；在屈服面上和屈服面外的部分对应塑性状态。 根据塑性力学的简化假设， 平均正应力σ_m=(σ₁ σ₂ σ₃)/3不影响屈服，所以，f在主应力空间中是以σ₁=σ₂=σ₃的直线为轴的一个等截面柱体，截面的形状可以在平面σ₁ σ₂ σ₃=0（称为π平面）上决定。

法国的H.特雷斯卡于1864年通过许多挤压实验研究屈服条件。他发现被挤压的金属上有许多很细的痕纹，它们的方向接近于最大剪应力的方向。他认为当最大剪应力τ达到某一极限值τY(称为剪切屈服极限)时，材料便进入屈服状态。这一屈服条件称为特雷斯卡条件或最大剪应力条件，其数学表达式为：

max(|σ₁-σ₂|，|σ₂-σ₃|，|σ₃-σ₁|)=2

等式左边表示取|σ₁-σ₂|、|σ₂-σ₃|、|σ₃-σ₁|中的最大者。等式在π平面上是一个正六边形(图2)。

德国的R.von米泽斯于1913年提出，在π平面可用一个圆代替特雷斯卡的正六边形(图2)，相应的屈服条件称为米泽斯条件，它避开了由于屈服面不光滑而带来的数学上的困难。米泽斯屈服条件的表达式为：

(σ₁-σ₂) (σ₂-σ₃) (σ₃-σ₁)=

后来，德国的H.亨奇提出，米泽斯屈服条件意味着在物体中的形变比能等于某一极限值时，材料就进入屈服状态。因此，米泽斯屈服条件又称为最大形变比能条件。

特雷斯卡屈服条件是一个线性的代数方程，知道主应力大小的次序后，使用这个条件比较方便；但在一般情况下事先并不知道主应力大小的次序，应用米泽斯屈服条件则比较方便，不过相应地要在数学上解一个非线性方程。

德国的W.洛德于1926年用薄壁管受拉伸和内压联合作用的试验验证屈服条件，他发现，对于碳素钢和合金钢等韧性材料，米泽斯屈服条件同试验结果符合得较好。

各向异性材料的屈服条件一般比较复杂，表达式中包含有反映材料各向异性性质的特征参量 。

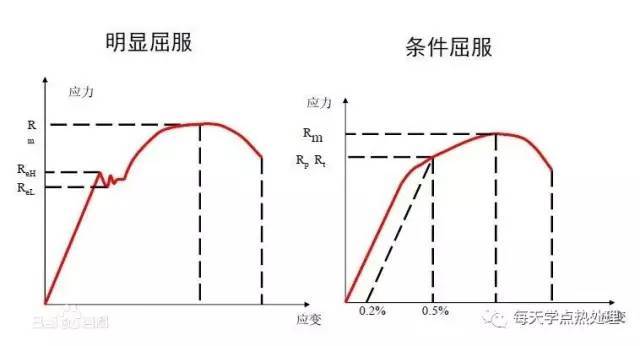
屈服强度：是金属材料发生屈服现象时的屈服极限，亦即抵抗微量塑性变形的应力。对于无明显屈服的金属材料，规定以产生0.2%残余变形的应力值为其屈服极限，称为条件屈服极限或屈服强度。大于此极限的外力作用，将会使零件永久失效，无法恢复。如低碳钢的屈服极限为207MPa，当大于此极限的外力作用之下，零件将会产生永久变形，小于这个的，零件还会恢复原来的样子。

（1）对于屈服现象明显的材料，屈服强度就是屈服点的应力（屈服值）；

（2）对于屈服现象不明显的材料，与应力-应变的直线关系的极限偏差达到规定值（通常为0.2%的原始标距）时的应力。通常用作固体材料力学机械性质的评价指标，是材料的实际使用极限。因为在应力超过材料屈服极限后产生颈缩，应变增大，使材料破坏，不能正常使用。

当应力超过弹性极限后，进入屈服阶段后，变形增加较快，此时除了产生弹性变形外，还产生部分塑性变形。当应力达到B点后，塑性应变急剧增加，应力应变出现微小波动，这种现象称为屈服。这一阶段的最大、最小应力分别称为上屈服点和下屈服点。由于下屈服点的数值较为稳定，因此以它作为材料抗力的指标，称为屈服点或屈服强度(R_eL或R_p0.2)。

有些钢材(如高碳钢)无明显的屈服现象，通常以发生微量的塑性变形(0.2%)时的应力作为该钢材的屈服强度，称为条件屈服强度。

首先解释一下材料受力变形。材料的变形分为弹性变形（外力撤销后可以恢复原来形状）和塑性变形（外力撤销后不能恢复原来形状，形状发生变化，伸长或缩短）。

建筑钢材以 屈服强度 作为设计应力的依据。

屈服极限 ，常用符号σ_s，是材料屈服的临界应力值。

（1）对于屈服现象明显的材料，屈服强度就是屈服点的应力（屈服值）；

（2）对于屈服现象不明显的材料，与应力-应变的直线关系的极限偏差达到规定值（通常为材料发生0.2%延伸率）时的应力。通常用作固体材料力学机械性质的评价指标，是材料的实际使用极限。因为在应力超过材料屈服极限后产生塑性变形，应变增大，使材料失效，不能正常使用。

当应力超过弹性极限后，进入屈服阶段后，变形增加较快，此时除了产生弹性变形外，还产生部分塑性变形。当应力达到B点后，塑性应变急剧增加，应力出现微小波动，这种现象称为屈服。这一阶段的最大、最小应力分别称为上屈服点和下屈服点。由于下屈服点的数值较为稳定，因此以它作为材料抗力的指标，称为屈服点或屈服强度(R_eL或R_p0.2)。

a．屈服点yield point（σ_s）

试样在试验过程中力不增加（保持恒定）仍能继续伸长（变形）时的应力。

b．上屈服点upper yield point（σ_su）

试样发生屈服而力首次下降前的最大应力。

c．下屈服点lower yield point（σ_sL）

当不计初始瞬时效应时屈服阶段中的最小应力。

有些钢材(如高碳钢)无明显的屈服现象，通常以发生微量的塑性变形(0.2%)时的应力作为该钢材的屈服强度，称为条件屈服强度。

首先解释一下材料受力变形。材料的变形分为弹性变形（外力撤销后可以恢复原来形状）和塑性变形（外力撤销后不能恢复原来形状，形状发生变化，伸长或缩短）

建筑钢材以 屈服强度 作为设计应力的依据。

所谓屈服，是指达到一定的变形应力之后，金属开始从弹性状态非均匀的向弹-塑性状态过渡，它标志着宏观塑性变形的开始。

无明显屈服现象的金属材料需测量其规定非比例延伸强度或规定残余伸长应力，而有明显屈服现象的金属材料，则可以测量其屈服强度、上屈服强度、下屈服强度。一般而言，只测定下屈服强度。

通常测定上屈服强度及下屈服强度的方法有两种：图示法和指针法。

屈服强度图示法

试验时用自动记录装置绘制力-夹头位移图。要求力轴比例为每mm所代表的应力一般小于10N/mm²，曲线至少要绘制到屈服阶段结束点。在曲线上确定屈服平台恒定的力F_e、屈服阶段中力首次下降前的最大力Feh或者不到初始瞬时效应的最小力F_eL。

屈服强度、上屈服强度、下屈服强度可以按以下公式来计算：

屈服强度计算公式：R_e=F_e/S_o；F_e为屈服时的恒定力。

上屈服强度计算公式：R_eh=F_eh/S_o；F_eh为屈服阶段中力首次下降前的最大力。

下屈服强度计算公式：R_eL=F_eL/S_o；F_eL为不到初始瞬时效应的最小力F_eL。

屈服强度指针法

试验时，当测力度盘的指针首次停止转动的恒定力或者指针首次回转前的最大力或者不到初始瞬时效应的最小力，分别对应着屈服强度、上屈服强度、下屈服强度。