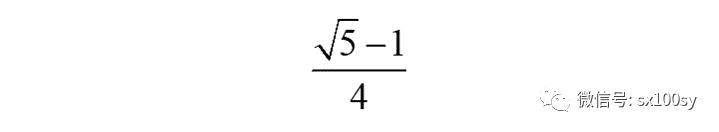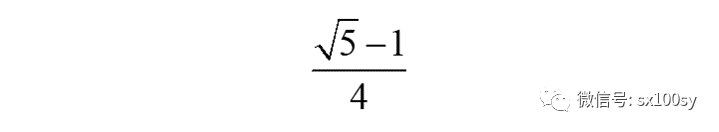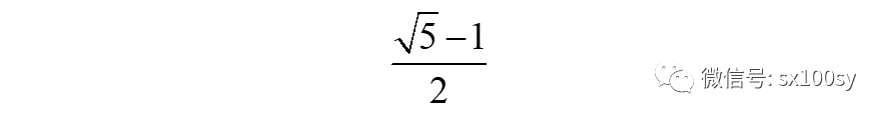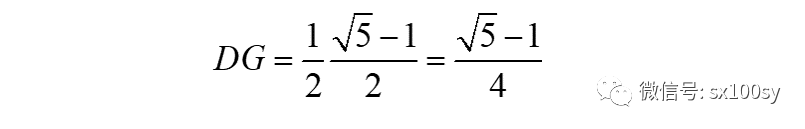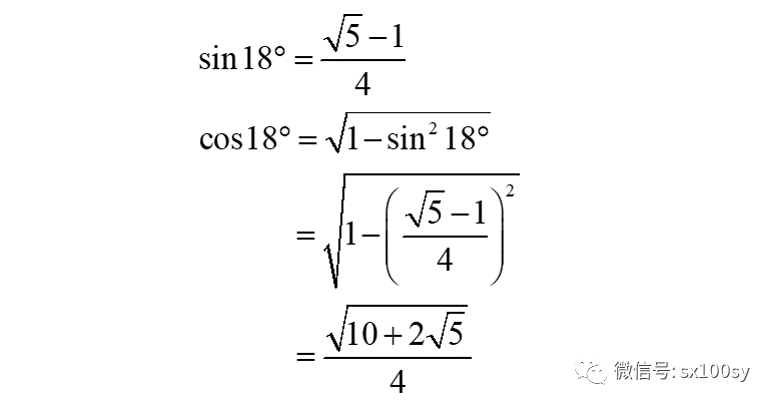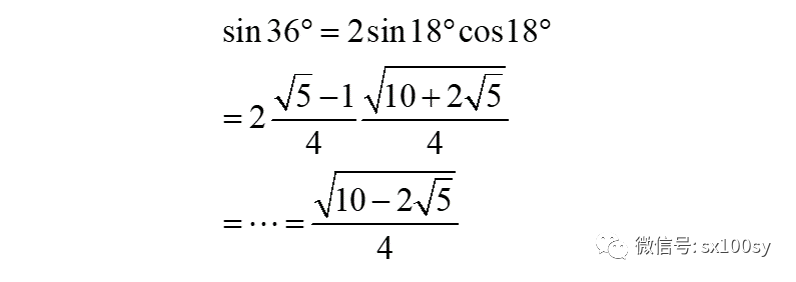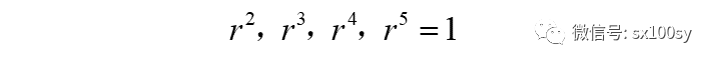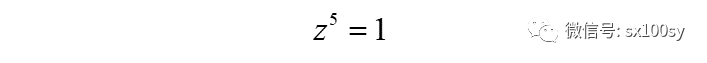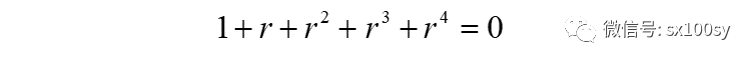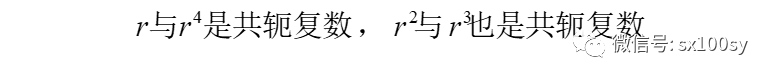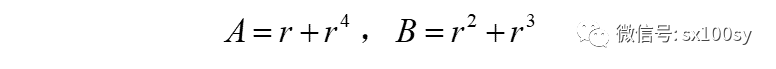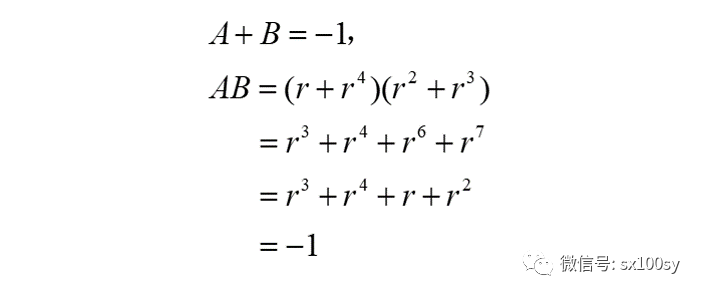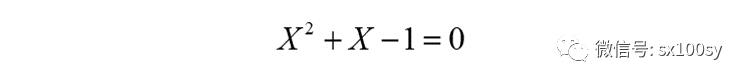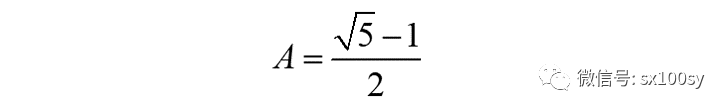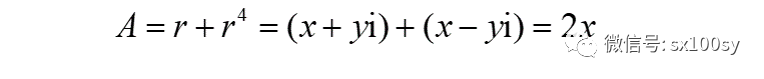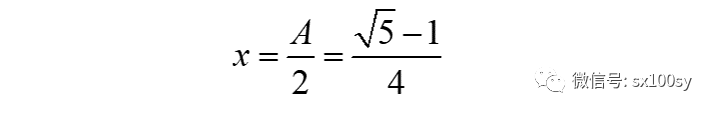尺规作图法(method of construction with rulerand compasses)亦称初等几何作图法或欧几里得作图法.初等几何所设定的作图方法.即仅限用直尺(无刻度)和圆规来完成几何作图的方法.在实际作图中，为提高作图速度和减少误差，有时也可用有刻度直尺、三角板、丁字尺、比例规、量角器等作为辅助工具作图，但必须以"作图成法"(基本作图题)为依据，并在作图题的"作法"步骤中给以明确叙述.

数学教学研究本公众号内容均由邵勇本人独创，可以转发，但转载则需获得邵勇本人的授权。每周推送两到三篇内容上有分量的数学文章，但在行文上力争做到深入浅出。几分钟便可读完，轻松学数学。

用尺规作图法，在已知一边的情况下画一个正五边形，这在之前的文章中讲过，比较容易。今天我们是用尺规作图法画圆内接正五边形，我们是不知道边长的（需要计算才能得到，文中也会讲到）。不失一般性，我们在单位圆内进行。并且，为了与单位根的概念一致，我们选取单位圆上最右侧的一点为正五边形的一个顶点。然后，我们需要确定其他四个顶点的位置，其实，只需确定与第一个顶点（位于点（1，0）处）相邻的一个顶点即可。

我们作互相垂直的两条直径：一条水平，一条竖直。我们让水平直径的右端点（下图中的点B）为所求作的正五边形的一个顶点。

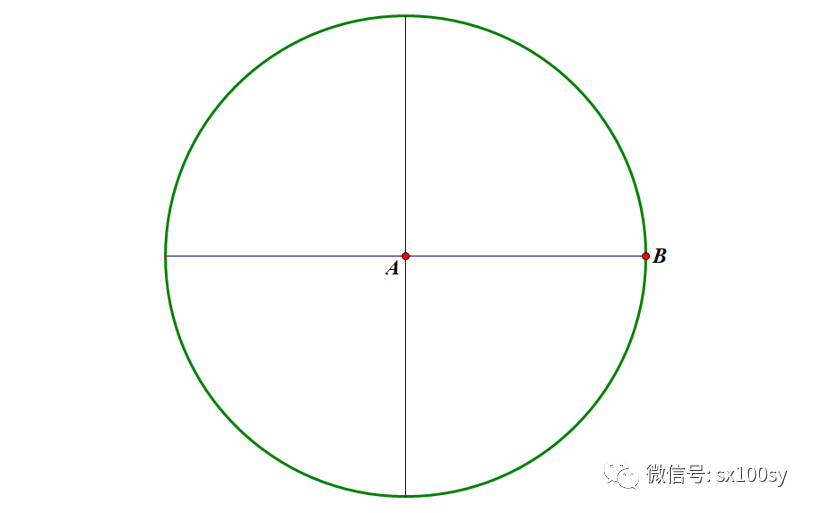
假设正五边形已经作出，如下图所示。则它的五个顶点到中心的连线把圆周角五等分，每个角都是72°。过与B相邻的顶点C作AB的垂线，交AB于点D。则三角形ACD为直角三角形，其中角ACD=18°。因为是单位圆，所以AC=1。所以，AD的长度就是sin18°。我们试着把sin18°求出来。

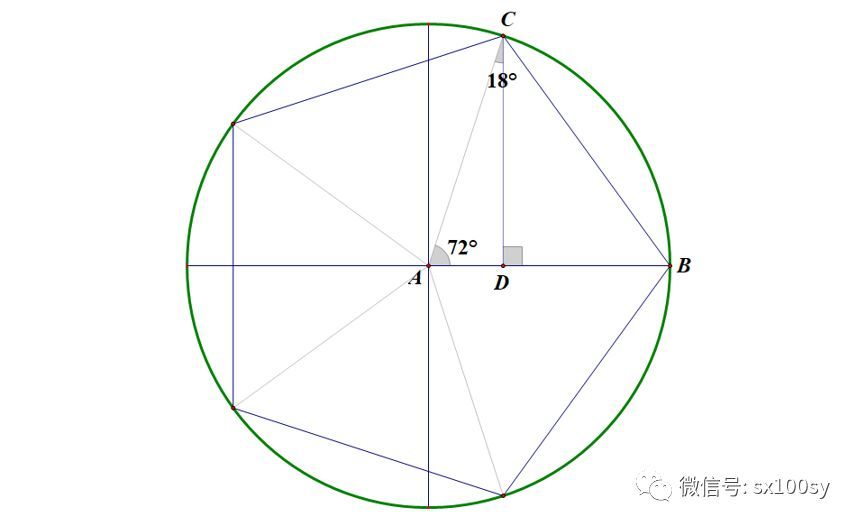
我们至少有两种求AD的方法。我先采用三角的方法（用复数的方法最后讲）。过程如下：

我们得到了AD=sin18°的根式表达式。所以，反过来，我们就可以根据这个值，作出到竖直直径距离为这个值的直线，它与单位圆的交点（在点B同侧的）就是所求作的正五边形的顶点。

上式结果中包括5的平方根，而一个正整数的平方根是可以通过尺规作图法画出来的。所以，我们可以说，sin18°是可以画出来的。具体如何画出根号5，只需让一个直角三角形的两条直角边分别为1和2，则斜边即为根号5。于是，用根号5减去1，所得线段取一半，再取一半的一半，就得到sin18°。最后在AB上量取AD等于这个值，得到点D。

上面的讨论从理论上解决了作圆内接正五边形是可以用尺规作图实现的。下面给出一种简洁的作图步骤，它可以快速得到点D。并且我将证明这种作图步骤是正确的。如下图所示，取半径AF的中点E，连接EB。作角AEB的平分线ED，点D为平分线与AB的交点。这个点D即为所求。然后过点D作AB的垂线，交单位圆于点C。则点C即为所求的正五边形的顶点。

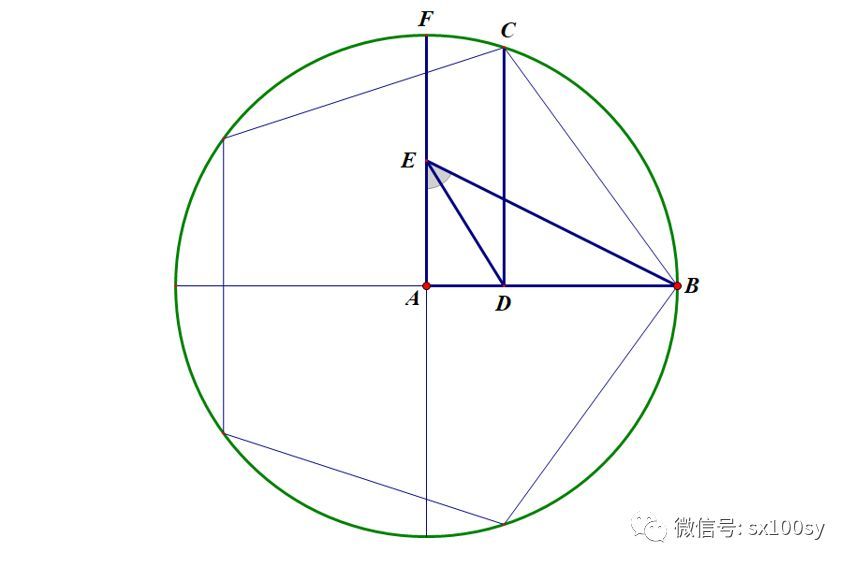
下面来证明这样作出来的AD的长度为

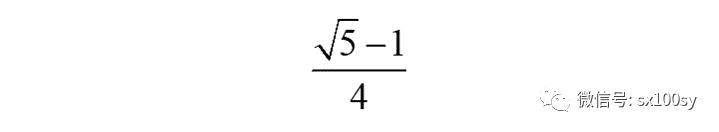
如下图所示。过点D作EB的垂线BG，G为垂足。于是，AD=DG。我们只需证明DG等于

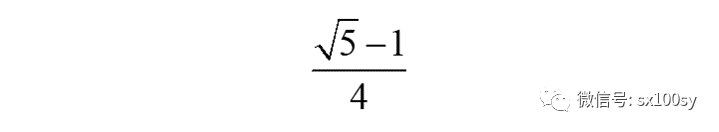
即可。

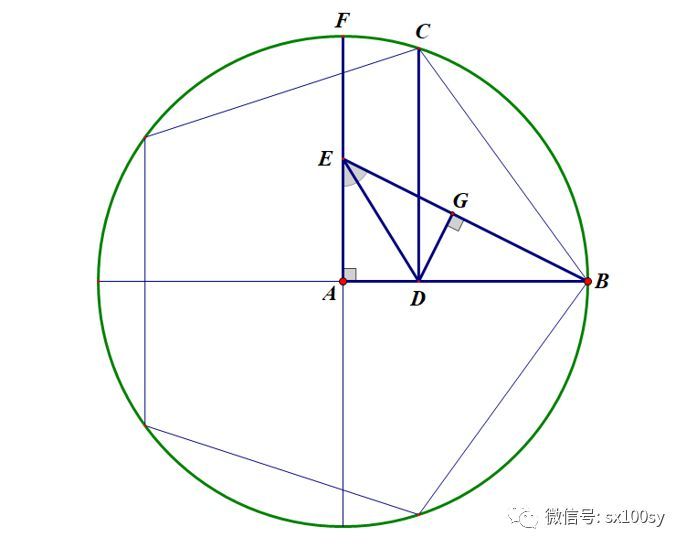
下面看一下图中已知的一些线段的长度：AB=1，AE=1/2，

也就是说，图中已经出现了

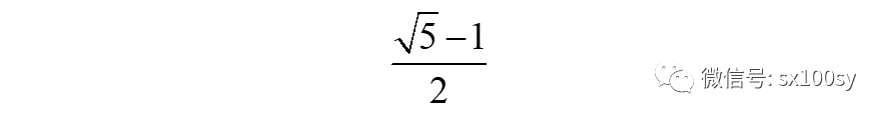
而三角形DGB与三角形AEB相似。所以，DG : GB = AE : AB。所以可以得到

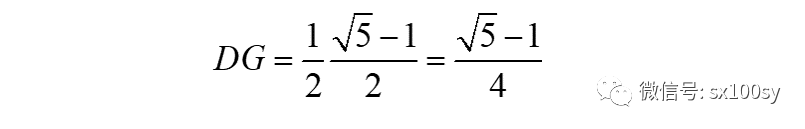
于是就证明了D点就是所求。

下面再介绍一种作图方法，这种方法是杜德尼发明的，它不是去确定如上面所说的某个顶点，而是确定出单位圆内接正五边形的边长，然后再用圆规确定出顶点位置。具体来说，仍然是取FA的中点E。然后以点E为圆心，以EB为半径作圆，与AH交于点K，则KB的长度即为单位圆内接正五边形的边长。下图中，BC=KB。点C即为正五边形的顶点。下面我们来证明BC的长度就是正五边形边的长度。

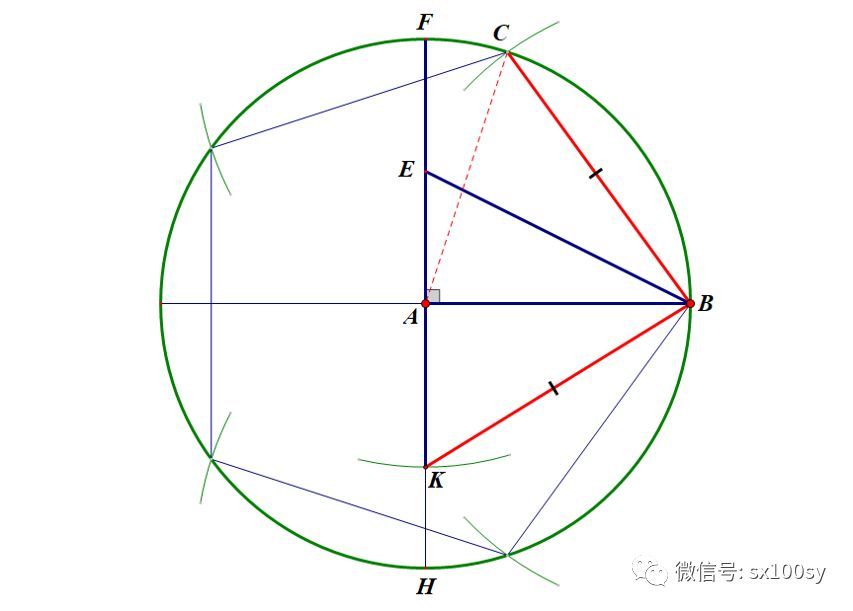
假设正五边形已经作出。如最初的那幅图所示（下图）。其中角BAC等于72°。过点A作BC的垂线AH，H为垂足。

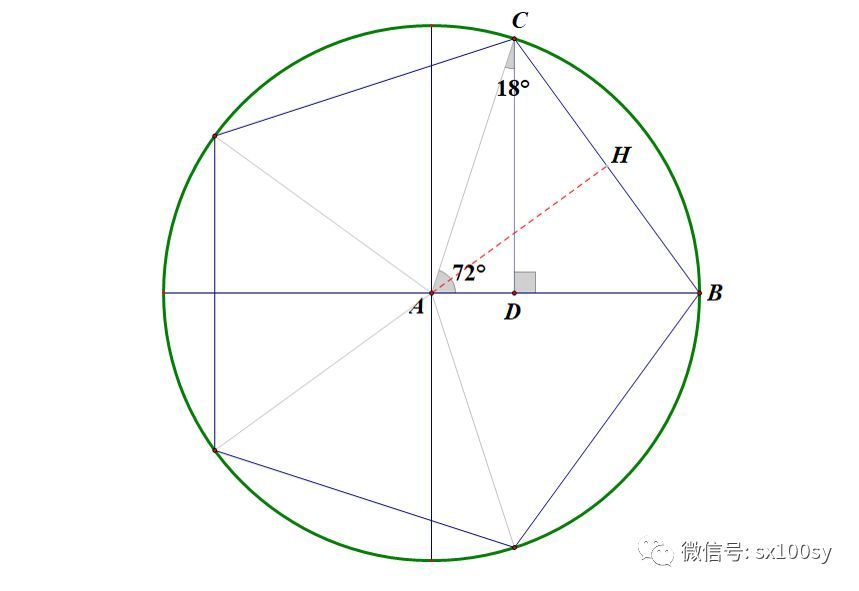
在直角三角形ACH中，AC=1，∠CAH=36°，所以，我们可以求出BC的一半CH。它等于sin36°。我们用三角公式求它的值。

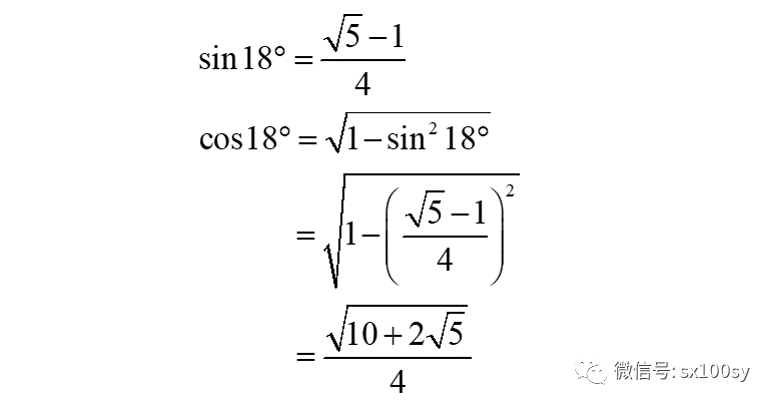
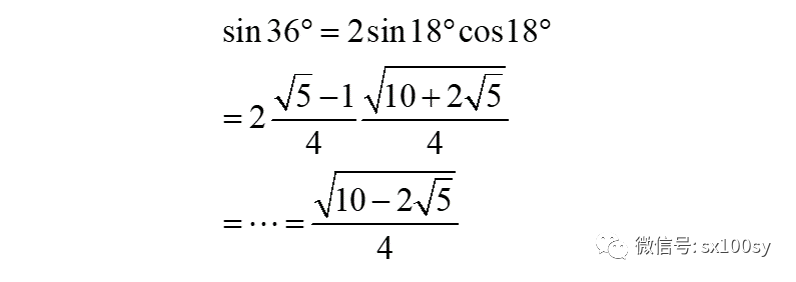
所以

这就是单位圆内接正五边形的边长。下面我们证明刚才我们作出的KB的长度也等于这个长度，这样一来我们的画法才能是正确的。如下图所示。

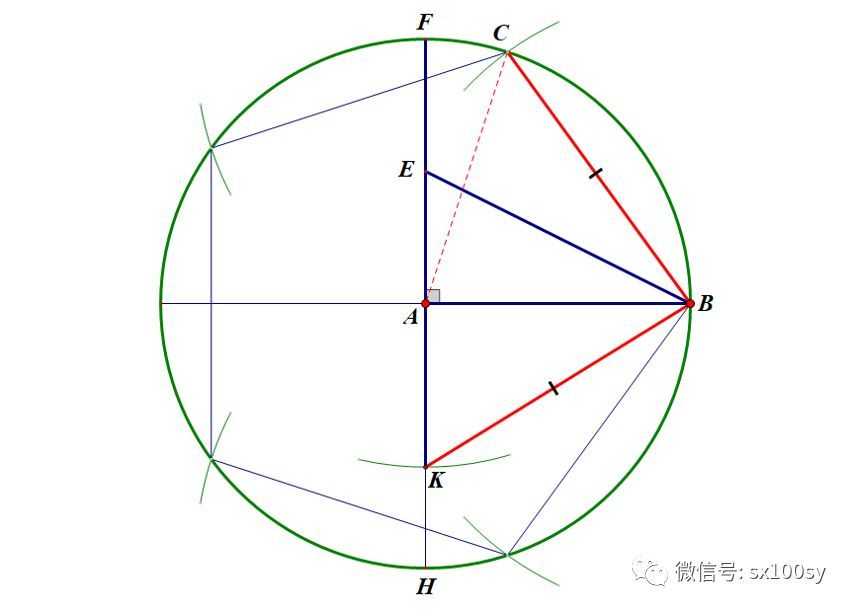
在上图中的直角三角形ABK中，

确实，KB等于单位圆内接正五边形的边长。证毕。

上述杜德尼的方法在很多书上都有介绍，而第一种作对角线的方法却不常见。我最早看到这个作法时，也不明白为什么对角线与AB的交点一下子就到位了。原来作对角线后，AD的长度正好是正五边形顶点C的横坐标（如果放在直角坐标系中看待），我认为这个方法比杜德尼的方法简洁。后来我又了解到高斯曾用单位根的方法求出了这个值（AD的长度）。下面简要叙述一下他的方法。

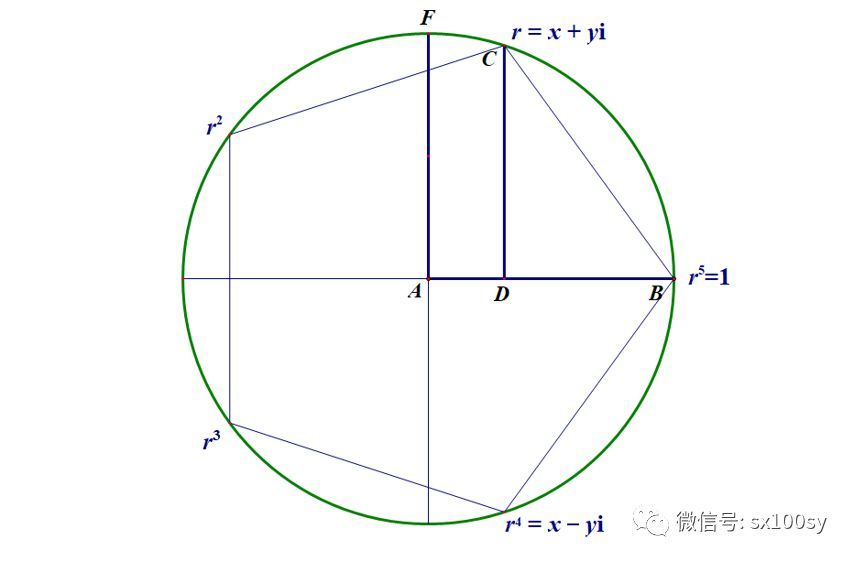
他是在复平面上来讨论的。也是假设正五边形已作出，如上图所示。把上图中点C用复数表示为r=x+yi，那么如果能求出x就可以了。其他四个顶点按逆时针，分别为

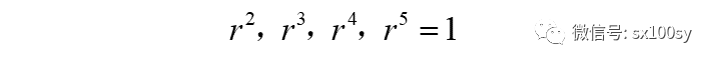
这五个复数就是方程

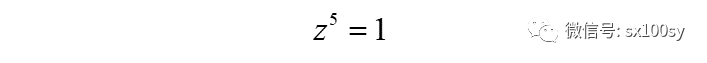
的五个根，我们叫它们为五次单位根。这些单位根不多不少只五个，且它们的模都为1。这五个单位根所表示的点把单位圆五等分。其中有一个根位于正实轴上。这五个单位根之间有一个关系，即

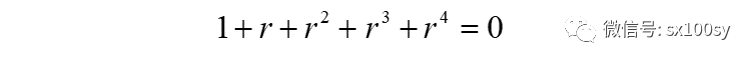
且

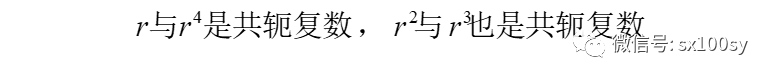
下面来求x。设

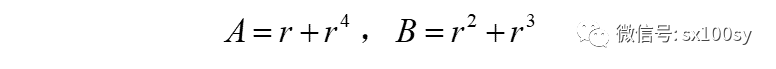
则有

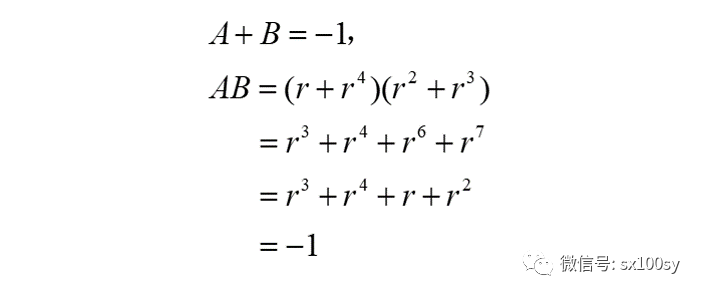
所以，由韦达定理，A和B是二次方程

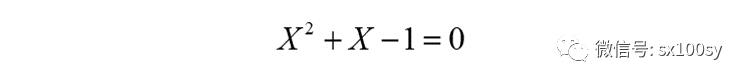
的两个实根。所以，可以求出

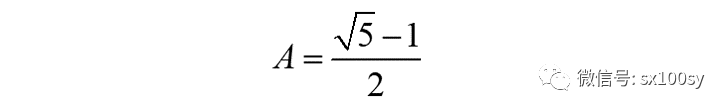
而

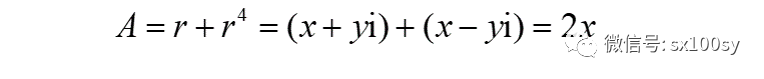
所以求出

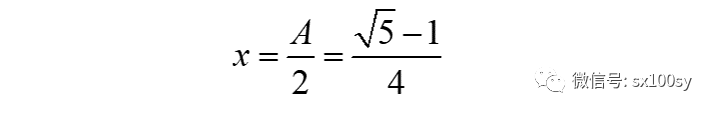
x就是顶点C处的复数r=x+yi的实部，也就是AD的长度。于是，反过来，我们便可以在实轴上作出点D使AD等于x。再过点D作实轴的垂线，与单位圆的交点就是正五边形的一个顶点。

本讲涉及内容很多，全是干货。请慢慢地、仔细地阅读和思考，相信会对您学习数学有所帮助的。

最后介绍两本小书，如下图。注意到没有，书名中都是《...谈起》，但这两个“起”字竟然不一样，那个”封口”的写法我也确实在其他地方见到过，不能算错，但碰巧我同时在看这两本书，无意中发现它们的不同。哈哈，很有趣！两本书的内容都是相当的好。很薄的两本小书，但内容一点儿都不”薄“ ！