相关实例
我国的房屋建筑采用采用三水准抗震设防目标，即“小震不坏，中震可修，大震不倒”。其中：
小震指该地区50年内超越概率约为63%的地震烈度，即众值烈度，又称多遇地震；
中震指该地区50年内超越概率约为10%的地震烈度，又称为基本烈度或设防烈度；
大震指该地区50年内超越概率约为2%～3%的地震烈度，又称罕遇地震。
如50年超越概率为63%相当于50年一遇；50年超越概率为10%相当于474年一遇；50年超越概率为2~3%相当于1600～2500年一遇。那么具体怎么换算呢？这得从地震活动性的随机过程描述模型说起。
描述地震活动性的随机过程模拟有很多，但目前应用最广泛的是泊松分布模型。泊松分布模型有三个基本特点：
1.独立性。亦即未来一段时间内事件是否发生与过去一段时间内事件是否发生无关。如今年是否发生地震与去年是否发生地震无关 ；
2.平稳性。亦即只要区段相等，则事件发生的概率与区段所处的位置无关，而仅与区段的大小有关。若所说的区段是指时间区段，则称这种性质为平稳性；若指空间区段，则称为均匀性。如某地区10年内发生地震的概率，无论这10年是在1900年~1910年还是2000年~2010年，都一样，只有时间间隔不同，如10年内与20年内相比，发生地震的概率才会不同；
3.不重复性。亦即事件集中在某一时间或空间发生的概率很小。如某一地区平均每年发生8级地震的概率为2%，则该地区一年内会发生2次8级地震的可能性很小，可以认为其概率几乎为0。
在t年内，某地区发生n次地震（不管震级大小）的概率P(n)，可用泊松分布表达如下：
P(n)=(vt)^n*exp(-vt)/n!
由上式易知，在t年内，某地区都不发生地震的概率为：
P(0)=(vt)^0*exp(-vt)/0!=exp(-vt)
则该地区在t年内至少发生一次地震的概率（此即为超越概率）为：
F(t)=1-P(0)=1-exp(-vt)
其概率密度f(t)为：
f(t)=F'(t)=vexp(-vt)
以上v为某地区地震年平均发生的概率，它与重现期T0为倒数关系，即：
T0=1/v
于是易得重现期T0与超越概率F(t)的关系为：
T0=1/v=-t/(ln(1-F(t))
由上式即可算出事件某时间段内各种超越概率的重现期。如t=50年，超越概率F(t)=10%的地震，其重现期为T0=474年。
以上给出的地震概率模型，仅关心地震是否发生，而不管震级M的大小。经对大量地震历史数据分析表明，震级M实际与地震年均发生的次数N存在一定的关系，常用下式表示：
N=exp(a-bM)或lnN=a-bM
a,b为经验常数。
震级M有着与地震发生的时间间隔t类似的概率分布，即其分布函数F(M)为：
F(M)=1-exp(-b(M-M0))
其分布密度f(M)为：
f(M)=b*exp(-b(M-M0))
M0为震级下限。如可监测到的震级为3级，则可取M0=3。
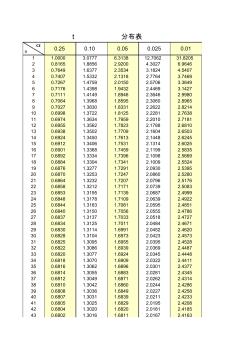概率论t分布表
加权系数概率值加权系数概率值