概率预算概率预算的编制文献

 财务预算的编制方法
财务预算的编制方法
财务预算的编制方法
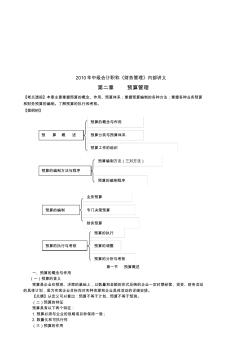
2010年中级会计职称《财务管理》内部讲义 第二章 预算管理 【考点透视】本章主要掌握预算的概念、作用、预算体系;掌握预算编制的各种方法;掌握各种业务预算 和财务预算的编制。了解预算的执行和考核。 【提纲树】 第一节 预算概述 一、预算的概念与作用 (一)预算的含义 预算是企业在预测、决策的基础上,以数量和金额的形式反映的企业一定时期经营、投资、财务活动 的具体计划,是为实现企业目标而对各种资源和企业具体活动的详细安排。 【点睛】从定义可以看出:预算不等于计划、预算不等于预测。 (二)预算的特征 预算具有以下两个特征: 1.预算必须与企业的战略或目标保持一致; 2.数量化和可执行性 (三)预算的作用 预 算 概 述 预算的概念与作用 预算分类与预算体系 预算工作的组织 预算的编制方法与程序 预算编制方法(三对方法) 预算的编制程序 预算的编制 业务预算 财务预算 专门决策预算 预算的执行与

 施工图预算的编制
施工图预算的编制
施工图预算的编制
施工图预算的编制 一、施工图预算的概念及其编制内容 (一 )施工图预算的含义及作用 1.施工图预算的含义 施工图预算是以施工图设计文件为依据,按照规定的程序、方法和依据,在工程施工前对工程项目 的工程费用进行的预测与计算。施工图预算的成果文件称作施工图预算书,也简称施工图预算,它是在 施工图设计阶段对工程建设所需资金作出较精确计算的设计文件。施工图预算价格既可以是按照政府统 一规定的预算单价、取费标准、计价程序计算得到的属于计划或预期性质的施工图预算价格,也可以是 通过招标投标法定程序后施工企业根据自身的实力即企业定额、资源市场单价以及市场供求及竞争状况 计算得到的反映市场 性质的施工图预算价格。 2.施工图预算的作用 施工图预算作为建设工程建设程序中一个重要的技术经济文件,在工程建设实施过程中具有十分重 要的作用,可以归纳为以下几个方面: (1) 施工图预算对投资方的作用。 1)施工图预