横截面回归法造价信息

市场价
信息价
询价

小截面塑力电缆

规格型号：
ZR-YJV22 4×6型号:ZR-YJV22;标称截面(mm2):6;芯数:4;额定电压:0.6/1KV;
价格行情：
材料单位：
m
材料品牌：
辽缆
材料税率：
13%
供应商：
沈阳辽缆电线电缆制造有限公司
报价时间：
2022-12-07

查看价格

柳安木自动回归防火门

规格型号：
自动回归甲级
价格行情：
材料单位：
m²
材料品牌：
材料税率：
13%
供应商：
上海正昊实业有限公司
报价时间：
2022-12-07

查看价格

经典回归瓷砖

规格型号：
系列:超级石材系列;品种:抛光砖600×600;用途:墙地砖;型号:G0AE-11EA;
价格行情：
材料单位：
块
材料品牌：
鹰牌
材料税率：
13%
供应商：
云南巨龙伟业建材有限公司
报价时间：
2022-12-07

查看价格

经典回归瓷砖

规格型号：
系列:超级石材系列;品种:抛光砖600×600;用途:墙地砖;型号:G0AC-21QEA;
价格行情：
材料单位：
块
材料品牌：
鹰牌
材料税率：
13%
供应商：
云南巨龙伟业建材有限公司
报价时间：
2022-12-07

查看价格

经典回归瓷砖

规格型号：
系列:超级石材系列;品种:抛光砖600×600;用途:墙地砖;型号:G0AM-21PEA;
价格行情：
材料单位：
块
材料品牌：
鹰牌
材料税率：
13%
供应商：
云南巨龙伟业建材有限公司
报价时间：
2022-12-07

查看价格

查看详情

1KV等截面VV电缆

规格型号：
单芯 2.5mm
价格行情：
材料单位：
m
材料税率：
地区时间：
深圳市2005年1月信息价
所属行业：
建筑工程
备注说明：

查看价格

1KV等截面VV电缆

规格型号：
单芯 6mm
价格行情：
材料单位：
m
材料税率：
地区时间：
深圳市2005年1月信息价
所属行业：
建筑工程
备注说明：

查看价格

1KV等截面VV电缆

规格型号：
单芯 120mm
价格行情：
材料单位：
m
材料税率：
地区时间：
深圳市2005年1月信息价
所属行业：
建筑工程
备注说明：

查看价格

1KV等截面VV电缆

规格型号：
单芯 300mm
价格行情：
材料单位：
m
材料税率：
地区时间：
深圳市2005年1月信息价
所属行业：
建筑工程
备注说明：

查看价格

1KV等截面VV电缆

规格型号：
两芯 6mm
价格行情：
材料单位：
m
材料税率：
地区时间：
深圳市2005年1月信息价
所属行业：
建筑工程
备注说明：

查看价格

查看详情

双向自动回归门(厨房专用)

规格型号：
1600×1200mm,不锈钢边框,5mm厚防撞胶板门扇,自闭弹簧门铰
需求量：
1m²
报价数：
1
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2015-11-26

查看价格

木龙骨截面

规格型号：
60×60 树池四
需求量：
6.2592m²
报价数：
3
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2016-03-22

查看价格

可变截面柱模

规格型号：
需求量：
9277t
报价数：
1
材料品牌：
材料档次：
普通
费用说明：
不含税费 | 不含运费
询价时间：
2015-11-05

查看价格

生态木截面

规格型号：
150x50
需求量：
1.0m²
报价数：
3
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2016-11-01

查看价格

木龙骨截面

规格型号：
40×60 木平台
需求量：
179.04m²
报价数：
3
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2016-03-22

查看价格

查看详情

横截面回归法计算

横截面回归法(CrossSectionRegressionMethod)什么是横截面回归法横截面回归法是由格林巴尔特和蒂特曼(1992)提出的，基本思路是检验一个评价期内的超额收益是否与接下来的持有期内的超额收益有正的相关关系。横截面回归法的计算[1]检验过程包括以下三个步骤。 (1)样本期间分为两个子期间，前一个期间为评价期，后一个期间为持有期。 (2)计算每只基金在两个子期间内的超额收益率，超额收益率用Jenson指数的α来衡量。 (3)将两个子期间的超额收益进行横截面回归，估计出回归的斜率系数，横截面回归的计算公式如下：αi,2=a bαi,1 εi公式中，a，b为回归系数，εi为随即误差项，αi,2,αi,1为持有期和评价期的超额收益率。回归结果中若b为正值且显著，则表明基金业绩具有持续性；反之，则表明基金业绩不具有持续性。参考文献深圳大学经济学院.经济学的时代问题[M].社会科学文献出版社,2010.073KAER.页面分类:基金绩效评价工具。

查看详情

横截面回归法常见问题

咋样把横截面变成竖截面

把你的问题说清楚一点。
横截面积

95就是选单芯最大的那个截面
什么叫横截面的面积？

我是第一个哦！比如说把一根木棒切成两半侧面就是。还不懂就补充在吗？懂了选我最佳答案。。。。。。你是六年级的吗？

查看详情

横截面回归法文献

电流与导线横截面关系

格式：pdf

大小：21KB

页数： 2页

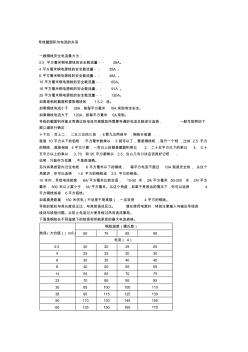
导线截面积与电流的关系一般铜线安全电流最大为： 2.5 平方毫米铜电源线的安全载流量－－ 28A。 4 平方毫米铜电源线的安全载流量－－ 35A 。 6 平方毫米铜电源线的安全载流量－－ 48A 。 10 平方毫米铜电源线的安全载流量－－ 65A。 16 平方毫米铜电源线的安全载流量－－ 91A 。 25 平方毫米铜电源线的安全载流量－－ 120A。如果是铝线截面积要取铜线的 1.5-2 倍。如果铜线电流小于 28A，按每平方毫米 10A来取肯定安全。如果铜线电流大于 120A，按每平方毫米 5A来取。导线的截面积所能正常通过的电流可根据其所需要导通的电流总数进行选择，一般可按照如下顺口溜进行确定：十下五 , 百上二 , 二五三五四三倍 ,七零九五两倍半 ,铜线升级算 . 就是 10 平方以下的铝线 ,平方毫米数乘以 5 就可以了 ,要是铜线呢 ,就升一个档 ,比如 2.

在线阅读立即下载

GFRP混凝土混合横截面楼板

格式：pdf

大小：21KB

页数： 2页

近年来,随着楼板耐久性要求的提高及建筑的快速发展,新的结构形式不断出现。提出解决建筑楼板问题的新成果,即玻璃纤维复合增强材料与混凝土相结合,采用钢螺栓及环氧层连接的方式。首先对采用两种剪切连接系统的截面玻璃纤维复合增强材料与混凝土试件进行剪切连接试验。试验的结果被用于设计带有玻璃纤维复合增强材料与混凝土混合横截面的简支梁,简支梁弯曲试验研究包括不同的跨长、不同的荷载组合。试验也包括不同支撑构造强度的研究。为更好地理解试验结果,即粘接系统混合梁界面的剥离机制,采用数值分析对界面的应力状态进行研究。试验和数值分析显示:玻璃纤维复合增强材料与混凝土混合横截面,无论是用在建筑楼板的修复还是新建筑上都具有很大的潜力,合理的细节设计能够显著改善系统的性能。

在线阅读立即下载

线性回归预测法定义

所谓线性回归模型就是指因变量和自变量之间的关系是直线型的。 回归分析预测法中最简单和最常用的是线性回归预测法。 回归分析是对客观事物数量依存关系的分析．是数理统计中的一个常用的方法．是处理多个变量之间相互关系的一种数学方法． 在现实世界中，我们常与各种变量打交道，在解决实际问题过程中，我们常常会遇到多个变量同处于一个过程之中，它们之间互相联系、互相制约．常见的关系有两种：一类为“确定的关系”即变量间有确定性关系，其关系可用函数表达式表示．例如：路程s,时间t,与速度v之间有关系式：s=vt 在圆体给与半径r之间有关系式v= 另外还有一些变量．他们之间也有一定的关系，然而这种关系并不完全确定，不能用函数的形式来表达，在这种关系中至少有一个变量是随机的．例如：人的身高与体重有一定的关系，一般来讲身高高的人体重相对大一些．但是它们之间不能用一个确定的表达式表示出来．这次变量（或至少其中有一个是随机变量）之间的关系．我们称之为相关关系．又如环境因素与农作物的产量也有相关关系，因为在相同环境条件下农作物的产量也有区别，这也就是说农作物的产量是一个随机变量．回归分析就是研究相关关系的一种数学方法，是寻找不完全确定的变量间的数学关系式并进行统计推断的一种方法．它能帮助我们从一个变量取得的值去估计另一个变量的值．在这种关系中最简单的是线性回归． 线性回归分析是对客观事物数量关系的分析，是一种重要的统计分析方法，被广泛的应用于社会经济现象变量之间的影响因素和关联的研究．由于客观事物的联系错综复杂经济现象的变化往往用一个变量无法描述，故本篇论文在深入分析一元线性回归及数学模型的情况下，又详细地介绍了多元线性回归方程的参数估计和其显著性检验等．全面揭示了这种复杂的依存关系，准确测定现象之间的数量变动．以提高预测和控制的准确度．

查看详情

自动散点控制回归法简介

自动散点控制回归法是由Elvidge等提出。假设两个时间的同一地点的像素值之间为线性关系，用两个时间同一光谱波段的数据绘制散点图,并拟合回归线;再用散点图定义不变点和无变化区，即将靠近回归线的像元视为在两个时段内的不变特征像元。 直方图匹配法是以一幅图像的直方图为基础，使原图像的灰度(亮度值)分布与参考图像的灰度分布情况相近(即转换一幅图像的直方图，使其和另一幅图像的直方图形状相似)从算法设计上是寻找一个灰度级变换的函数。一般是建立两个图像均值和方差之间的线性关系。

查看详情

线性回归预测法线性模型

一元线性回归分析预测法，是根据自变量x和因变量Y的相关关系，建立x与Y的线性回归方程进行预测的方法。由于市场现象一般是受多种因素的影响，而并不是仅仅受一个因素的影响。所以应用一元线性回归分析预测法，必须对影响市场现象的多种因素做全面分析。只有当诸多的影响因素中，确实存在一个对因变量影响作用明显高于其他因素的变量，才能将它作为自变量，应用一元相关回归分析市场预测法进行预测。 一元线性回归分析法的预测模型为： 式中，xt代表t期自变量的值； 代表t期因变量的值； a、b代表一元线性回归方程的参数。 a、b参数由下列公式求得（用代表）： 为简便计算，我们作以下定义： 式中： 这样定义a、b后，参数由下列公式求得： 将a、b代入一元线性回归方程Yt = a bxt，就可以建立预测模型，那么，只要给定xt值，即可求出预测值。 在回归分析预测法中，需要对X、Y之间相关程度作出判断，这就要计算相关系数Y，其公式如下： 相关系数r的特征有： ①相关系数取值范围为：-1≤r≤1 。 ②r与b符合相同。当r>0，称正线性相关，Xi上升，Yi呈线性增加。当r0.7，为高度线性相关；0.32100433B

查看详情

热门搜索

造价通

横截面回归法

横截面回归法基本信息

横截面回归法定义

横截面回归法造价信息

小截面塑力电缆

柳安木自动回归防火门

经典回归瓷砖

经典回归瓷砖

经典回归瓷砖

1KV等截面VV电缆

1KV等截面VV电缆

1KV等截面VV电缆

1KV等截面VV电缆

1KV等截面VV电缆

双向自动回归门(厨房专用)

木龙骨截面

可变截面柱模

生态木截面

木龙骨截面

横截面回归法计算

横截面回归法常见问题

横截面回归法文献

线性回归预测法定义

自动散点控制回归法简介

线性回归预测法线性模型

相关推荐