静定反力文献

 超静定结构支座反力计算的单位支座位移法
超静定结构支座反力计算的单位支座位移法
超静定结构支座反力计算的单位支座位移法
将单位支座位移法推广应用于超静定结构的未知支座反力计算,建立并证明了相应的退化虚位移方程,推导指出超静定结构支座反力的影响线即为相应单位支座位移所引起的位移曲线。而且,展示了几个求解超静定梁支座反力的算例.本文工作可供大学生和教师们在结构力学相关知识的学习和教学中借鉴参考.

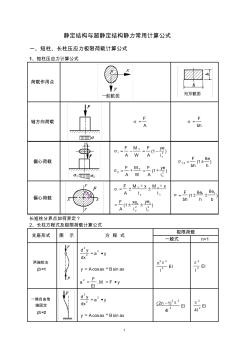 静定结构与超静定结构静力计算公式
静定结构与超静定结构静力计算公式
静定结构与超静定结构静力计算公式
1 静定结构与超静定结构静力常用计算公式 一、短柱、长柱压应力极限荷载计算公式 1、短柱压应力计算公式 荷载作用点 轴方向荷载 A F bh F 偏心荷载 )1( 21 x Y i ye A F W M A F )1( 22 x Y i ye A F W M A F ) 6 1(2,1 h e bh F 偏心荷载 )1( 22 x y y x x x y Y i ye i xe A F I xM I xM A F ) 66 1( b e h e bh F yx 长短柱分界点如何界定? 2、长柱方程式及极限荷载计算公式 支座形式 图 示 方 程 式 极限荷载 一般式 n=1 两端铰支 β=1 ya dx yd 2 2 2 axBaxAy sincos yFM EI F a ,2 EI l n 2 22 EI l 2 2 一端自由他 端固定 β=2 ya dx yd 2 2 2 axB