静面积矩文献

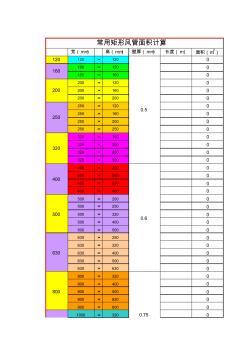 常用矩形风管面积计算表
常用矩形风管面积计算表
常用矩形风管面积计算表
宽(mm) 高(mm) 壁厚(mm) 长度(m) 面积(m2) 120 120 × 120 0 160 × 120 0 160 × 160 0 200 × 120 0 200 × 160 0 200 × 200 0 250 × 120 0 250 × 160 0 250 × 200 0 250 × 250 0 320 × 160 0 320 × 200 0 320 × 250 0 320 × 320 0 400 × 200 0 400 × 250 0 400 × 320 0 400 × 400 0 500 × 200 0 500 × 250 0 500 × 320 0 500 × 400 0 500 × 500 0 630 × 250 0 630 × 320 0 630 × 400 0 630 × 500 0 630 × 630 0 800 × 320 0 800 × 400 0 800

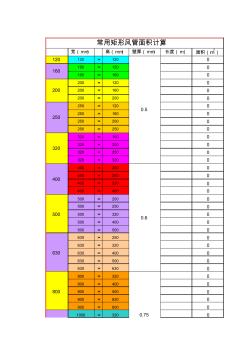 常用矩形风管面积计算表 (2)
常用矩形风管面积计算表 (2)
常用矩形风管面积计算表 (2)
宽(mm) 高(mm) 壁厚(mm) 长度(m) 面积(m2) 120 120 × 120 0 160 × 120 0 160 × 160 0 200 × 120 0 200 × 160 0 200 × 200 0 250 × 120 0 250 × 160 0 250 × 200 0 250 × 250 0 320 × 160 0 320 × 200 0 320 × 250 0 320 × 320 0 400 × 200 0 400 × 250 0 400 × 320 0 400 × 400 0 500 × 200 0 500 × 250 0 500 × 320 0 500 × 400 0 500 × 500 0 630 × 250 0 630 × 320 0 630 × 400 0 630 × 500 0 630 × 630 0 800 × 320 0 800 × 400 0 800
