角平分线性质定理
角平分线的性质:
1.角平分线可以得到两个相等的角。
2.角平分线上的点到角两边的距离相等。
3.三角形的三条角平分线交于一点,称作三角形内心。三角形的内心到三角形三边的距离相等。
4.三角形一个角的平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。
-

选择特殊符号
选择搜索类型
请输入搜索
角平分线的性质:
1.角平分线可以得到两个相等的角。
2.角平分线上的点到角两边的距离相等。
3.三角形的三条角平分线交于一点,称作三角形内心。三角形的内心到三角形三边的距离相等。
4.三角形一个角的平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。

【角平分线逆定理】
1.到角两边的距离相等的点在角平分线上。
2.平面内任意一小于180度的∠MAN如图,直线BC分别交半直线AM、AN、AS于B、C、D,AB/BD=AC/CD则:AS平分∠MAN
下面给出证明过程:
证明:过B作BH∥AC交AS于H
∴△ADC∽△HDB(∠ADC=∠HDB,∠ACD=∠HBD)
∴AC/CD=HB/BD
又AB/BD=AC/CD
∴AB=BH
∴∠BHA=∠BAH=∠HAC
∴AS平分∠MAN

●三角形内角平分线分对边所成的两条线段,和两条邻边成比例.
即 在三角形ABC中,当AD是顶角A的角平分线交底边于D时,BD/CD=AB/AC.
证明
:
如图,AD为△ABC的角平分线,过点D向边AB,AC分别引垂线DE,DF.则DE=DF.
S△ABD:S△ACD=BD/CD
又因为S△ABD:S△ACD=[(1/2)AB×DE]:[(1/2)AC×DF]=AB:AC
所以BD/CD=AB/AC.
1.角平分线可以得到两个相等的角。
角平分线,顾名思义,就是将角平分的射线。
如右图,若射线AD是角CAB的角平分线,则角CAD等于角BAD。
2.角平分线线上的点到角两边的距离相等。
如右上图,若射线AD是∠CAB的角平分线,求证:CD=BD
∵∠DCA=∠DBA
∠CAD=∠BAD
AD=AD
∴△ACD≌△ABD
∴CD=BD
3.三角形的三条角平分线交于一点,称作三角形的内心。三角形的内心到三角形三边的距离相等。
这一条是第二条的引申,详细证明过程参照第二条和三角形内心。
4.三角形一个角的平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。
如右下图,平面内任意一小于180度的∠MAN,AS平分∠MAN,直线BC分别交射线AM、AN、AS于B、C、D,求证:AB/BD=AC/CD:
作BE=BD交射线AS于E,如图1:
∵BE=BD,
∴∠BED=∠BDE,
∴∠AEB=∠ADC
又∵∠BAE=∠CAD,
∴△AEB∽△ADC,
∴AB/BE=AC/CD, 即AB/BD=AC/CD.
另外的情况,
如图2,直线BC交AS的反向延长线于D,
如图3,直线BC交AN的反向延长线于C;
此时,仍有AB/BD=AC/CD
证法与图1类似

三角形外角定理证明过程; http://zhidao.baidu.com/question/59352008.html?si=1三角形内角定理:(1)角的平分线是到角的两边距离相等的所有点的集合.∠A...
没有圆切角定理,只有弦切角定理:弦切角等于它所夹的弧对的圆周角
首先更正一下,是弦切角,老沈瞎说呢。你把图画出来,AB是圆O切线,AC是弦。做过切点A的直径,交圆O于A、D。连接B、D。证明:因为AD是圆O直径,AB是圆O切线所以∠C=90°=∠BAD所以∠BAC...

 鲁教版六年级下册线段中点与角平分线练习(无答案)
鲁教版六年级下册线段中点与角平分线练习(无答案)
鲁教版六年级下册线段中点与角平分线练习(无答案)
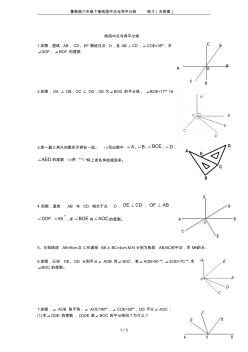
鲁教版六年级下册线段中点与角平分线 练习(无答案) 1 / 3 线段中点与角平分线 1.如图,直线 AB、CD、EF 都经过点 O,且 AB⊥CD,∠COE=35°,求 ∠DOF、∠BOF 的度数. 2.如图,OA 丄 OB,OC 丄 OD,OE 为∠BOD 的平分线, ∠BOE=17° 18 3.把一副三角尺如图所示拼在一起。 ⑴写出图中 A、 B、 BCE、 D、 AED的度数;⑵用 “ ”将上述各角连接起来。 4.如图,直线 AB 与 CD 相交于点 O, CDOE , ABOF , 65DOF ,求 BOE与 AOC的度数。 5、已知线段 AB=6cm,点 C在直线 AB上,BC=4cm,M,N分别为线段 AB,BC的中点 ,求 MN的长 . 6.如图,已知 OE、OD 分别平分∠ AOB 和∠ BOC,若∠ AOB=90°,∠EOD=70°,求 ∠BOC 的度数。 7.如图,

 蝴蝶定理线束夹角表达形式的研究
蝴蝶定理线束夹角表达形式的研究
蝴蝶定理线束夹角表达形式的研究
利用射影几何有关线束与点列的交比关系,给出广义蝴蝶定理的线束夹角的三角函数及斜率表示形式,并且统一给出蝴蝶定理的线段表示新形式.
三角形内外角平分线性质定理:三角形的内外角平分线内、外分对边与其延长线所得的两条线段与夹这个角的两边对应成比例。 2100433B