●三角形内角平分线分对边所成的两条线段，和两条邻边成比例.

即 在三角形ABC中，当AD是顶角A的角平分线交底边于D时，BD/CD=AB/AC.

证明

:

如图，AD为△ABC的角平分线，过点D向边AB,AC分别引垂线DE,DF.则DE=DF.

S△ABD:S△ACD=BD/CD

又因为S△ABD:S△ACD=[(1/2)AB×DE]:[(1/2)AC×DF]=AB:AC

所以BD/CD=AB/AC.

1.角平分线可以得到两个相等的角。

角平分线，顾名思义，就是将角平分的射线。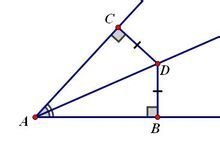

如右图，若射线AD是角CAB的角平分线，则角CAD等于角BAD。

2.角平分线线上的点到角两边的距离相等。

如右上图，若射线AD是∠CAB的角平分线，求证:CD=BD

∵∠DCA=∠DBA

∠CAD=∠BAD

AD=AD

∴△ACD≌△ABD

∴CD=BD

3.三角形的三条角平分线交于一点，称作三角形的内心。三角形的内心到三角形三边的距离相等。

这一条是第二条的引申，详细证明过程参照第二条和三角形内心。

4.三角形一个角的平分线，这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。

如右下图，平面内任意一小于180度的∠MAN，AS平分∠MAN，直线BC分别交射线AM、AN、AS于B、C、D，求证:AB/BD=AC/CD:

作BE=BD交射线AS于E，如图1:

∵BE=BD，

∴∠BED=∠BDE，

∴∠AEB=∠ADC

又∵∠BAE=∠CAD,

∴△AEB∽△ADC,

∴AB/BE=AC/CD, 即AB/BD=AC/CD.

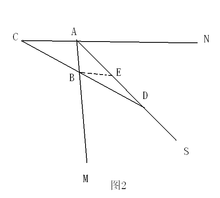
另外的情况，

如图2，直线BC交AS的反向延长线于D,

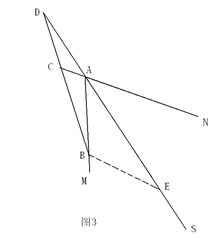
如图3，直线BC交AN的反向延长线于C;

此时，仍有AB/BD=AC/CD

证法与图1类似