卡尔瓦利亚树分布情况文献

 卡尔斯玛钢管件1
卡尔斯玛钢管件1
卡尔斯玛钢管件1
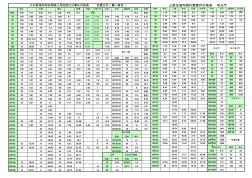
弯头 三通 管古 四通 快接 快接三通 对丝 活节 45度弯 丝堵 丝堵 规格 弯头 三通 管古 四通 内外弯 外丝 活节 45度弯 内外管 古 规格 包装 单价 包装 单价 包装 单价 单价 带边 配套 15 1.15 1.76 0.99 2.9 1.86 1.05 3.09 1.05 1.57 15 350 0.85 200 1.3 500 0.7 9.84 11.29 0.65 1.96 0.78 0.3 0.27 20 1.74 2.45 1.28 4.8 3.27 1.42 4.14 1.74 2.7 20 200 1.22 150 1.89 350 1.1 2.97 14.06 15.23 0.9 2.49 1.2 0.47 0.4 25 2.79 4 2.03 6.85 4.3 2 6 2.8 3.5 25 150 2.06 100 3.01 250 1.65 4.21 16
