水准仪交叉误差的检验文献

 水准仪i角的检验
水准仪i角的检验
水准仪i角的检验
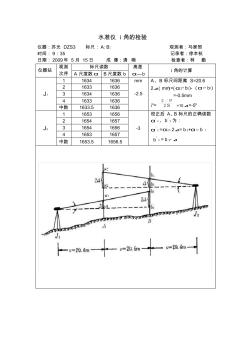
水准仪 i 角的检验 仪器:苏光 DZS3 标尺: A: B: 观测者:马家恒 时间: 9:35 记录者:徐本杭 日期: 2009年 5月 15日 成 像:清 晰 检查者:林 勤 仪器站 观测 次序 标尺读数 高差 α—b i 角的计算 A 尺度数α B尺度数 b J1 1 1634 1636 mm -2.5 A、B 标尺间距离 S=20.6 2⊿(mm)=(α 2- b2)- (α 1- b1) =-0.5mm i"= =10⊿=-5" 2 1633 1636 3 1634 1636 4 1633 1636 中数 1633.5 1636 J2 1 1653 1656 -3 校正后 A、B 标尺的正确读数 α / 2 、b / 2 为: α / 2 =α2- 2⊿= b 2+α 1- b 1 b / 2 = b 2-⊿ 2 1654 1657 3 1654 1

 水准仪
水准仪
水准仪
D 表示“大地” S 表示“水准仪”,就是水准仪拼音的开头 3 代表每公里往、返测量高差平均值的中误差不超过 ±3mm. 水准仪后面的数字: “05”、“1”、“3”、“10”等数字表示该仪器的精度。 S05 级和 S1级水准仪称为精密水准仪,用于国家一、二等精密水准测量。 S3级和 S10级 水准仪又称为普通水准仪,用于我国国家三、四等水准及普通水准测量。 所以, DS3 大地水准仪,是普通水准仪, DS3是型号的全称,而 S3和 DS3是 相同的,只是 S3这个型号没有写全,实际是把 DS3简写成了 S3而已。 前视 距离 =(前视上丝 - 前视下丝) *100 如果有红黑面 就上面红黑面各一次 然后求平均值 后视距离同理 (仪器肯定是要整平的)