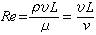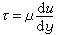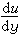紊流强度造价信息

市场价
信息价
询价

高强度竹基纤维墙板

规格型号：
100×10mm
价格行情：
材料单位：
m²
材料品牌：
竹钢®
材料税率：
13%
供应商：
洪雅竹元科技有限公司
报价时间：
2022-12-08

查看价格

高强度竹基纤维墙板

规格型号：
120×20mm
价格行情：
材料单位：
m²
材料品牌：
竹钢®
材料税率：
13%
供应商：
洪雅竹元科技有限公司
报价时间：
2022-12-08

查看价格

高强度竹基纤维栏杆

规格型号：
立柱1250×100×100mm@1250mm、扶手2500×50×40mm横条2500×60×10 mm、立条830×40×20mm
价格行情：
材料单位：
m
材料品牌：
竹钢®
材料税率：
13%
供应商：
洪雅竹元科技有限公司
报价时间：
2022-12-08

查看价格

高强度竹基纤维栏杆

规格型号：
立柱1250×80×80mm@1250mm、扶手2500×50×40mm横条2500×60×10 mm、立条830×40×20mm
价格行情：
材料单位：
m
材料品牌：
竹钢®
材料税率：
13%
供应商：
洪雅竹元科技有限公司
报价时间：
2022-12-08

查看价格

高强度竹基纤维栏杆

规格型号：
立柱1250×150×150mm@3000mm、扶手3000×100×100mm横条2500×100×20 mm、立条940×100×20mm
价格行情：
材料单位：
m
材料品牌：
竹钢®
材料税率：
13%
供应商：
洪雅竹元科技有限公司
报价时间：
2022-12-08

查看价格

查看详情

高强度彩色复合

规格型号：
400×400×60本色
价格行情：
材料单位：
m²
材料税率：
地区时间：
深圳市2005年7月信息价
所属行业：
建筑工程
备注说明：

查看价格

高强度彩色复合

规格型号：
400×400×60白色、黄色
价格行情：
材料单位：
m²
材料税率：
地区时间：
深圳市2005年7月信息价
所属行业：
建筑工程
备注说明：

查看价格

高强度彩色复合

规格型号：
400×400×60 116#红色
价格行情：
材料单位：
m²
材料税率：
地区时间：
深圳市2005年7月信息价
所属行业：
建筑工程
备注说明：

查看价格

高强度彩色复合

规格型号：
400×400×60 110#红色
价格行情：
材料单位：
m²
材料税率：
地区时间：
深圳市2005年7月信息价
所属行业：
建筑工程
备注说明：

查看价格

高强度彩色复合

规格型号：
400×400×80白色、黄色
价格行情：
材料单位：
m²
材料税率：
地区时间：
深圳市2005年7月信息价
所属行业：
建筑工程
备注说明：

查看价格

查看详情

立式紊流搅拌机

规格型号：
LJ40A
需求量：
2台
报价数：
1
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2010-10-19

查看价格

高强度密封索

规格型号：
强度:1570级
需求量：
1t
报价数：
2
材料品牌：
材料档次：
中高档
费用说明：
不含税费 | 含运费
询价时间：
2019-11-06

查看价格

骨骼强度

规格型号：
展项通过观众的亲身体验,向观众展示了骨骼的强度.展项由模型,互动装置及说明牌组成,参观者首先观看说明牌及模型,然后按压手柄,观看压力数值.超过骨骼可承受的压力时,骨骼模型将利用灯光、裂缝演示骨骼碎裂.
需求量：
1项
报价数：
1
材料品牌：
材料档次：
中高档
费用说明：
含税费 | 含运费
询价时间：
2022-09-16

查看价格

骨骼强度

规格型号：
展项通过观众的亲身体验,向观众展示了骨骼的强度.展项由模型,互动装置及说明牌组成,参观者首先观看说明牌及模型,然后按压手柄,观看压力数值.超过骨骼可承受的压力时,骨骼模型将利用灯光、裂缝演示骨骼碎裂.
需求量：
1项
报价数：
1
材料品牌：
材料档次：
高档
费用说明：
不含税费 | 含运费
询价时间：
2022-09-14

查看价格

骨骼强度

规格型号：
展项通过观众的亲身体验,向观众展示了骨骼的强度.展项由模型,互动装置及说明牌组成,参观者首先观看说明牌及模型,然后按压手柄,观看压力数值.超过骨骼可承受的压力时,骨骼模型将利用灯光、裂缝演示骨骼碎裂.
需求量：
1项
报价数：
1
材料品牌：
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2022-08-15

查看价格

查看详情

紊流强度常见问题

压力补偿式滴头和紊流器的区别?

紊流器属于一种压力补偿式滴头，它的体型小，流量低，外形酷似纽扣压力补偿滴头安装，因此被形象的称作纽扣式压力补偿滴头。紊流器一般安装在PE管材之上，作为滴灌器材末端灌水器使用供应压力补偿滴头，同时...
什么叫做电流强度

科学上把单位时间里通过导体任一横截面的电量叫做电流强度，简称电流。通常用字母 I表示，它的单位是安培（安德烈·玛丽·安培），1775年—1836年，法国物理学家、化学家，在电磁作用方面的研究成就卓著，...
流水施工流水强度是指什么

每一工序（每一施工段）相互衔接，则每一工序（每一施工段）则为流水段，相互衔接施工则为流水。每一段的量与施工人力、物力机械设备的投入量与自有资源的比较则为强度，即按这样的流水按排，本企业现有资料是否能完...

查看详情

紊流强度文献

紊流对粘性细颗粒泥沙絮凝影响

格式：pdf

大小：407KB

页数：未知

以分形聚集生长模型为基础,通过三维模拟泥沙颗粒在布朗运动、重力沉降和紊流作用下的碰撞、粘结和破碎过程,探讨了紊流对粘性细颗粒泥沙絮凝速度、絮团平均粒径及分形维数的时空影响。试验结果表明:紊流作用下,泥沙絮凝及絮团平均粒径的变化可分为加速段、等速段和减速段,絮凝等速段的作用时间及粒径等速增长段的速度均随紊动强度呈先增后减的规律,且中部区域的絮凝速度和絮团平均粒径较小;泥沙絮团分形维数随水流紊动强度的增加逐渐增大,最终趋于稳定,随时间呈先减后增的规律。模拟空间下部区域分形维数最大,上部次之,中部最小。

在线阅读立即下载

泄水建筑物曲面边壁紊流数值分析

格式：pdf

大小：407KB

页数：未知

采用先进的数值计算技术求解完整的Ｎａｖｉｅｒ－Ｓｔｏｋｅｓ方程，辅以双方程紊流ｋ－ε模型，并计入流线弯曲的影响，模拟泄水建筑物曲面边壁紊流的水力特性。实例计算结果与物理模型实测资料符合较好，证明该数学模型可用于预测泄水建筑物曲面边壁紊流的水力特性。

在线阅读立即下载

层流和紊流概述

正文 雷诺数表征液流惯性力与粘滞力相对大小，可用以判别流动形态的无因次数，记作Re。雷诺数的定义式为： 式中ρ、μ、ν分别为液体的密度、动力粘滞系数、运动粘滞系数；ν、L为流动的特征速度和特征长度。雷诺数小时,粘性效应在整个流场中起主要作用,流动为层流。雷诺数大时，紊动混掺起决定作用，流动为紊流。对于同样的液流装置，由层流转换为紊流时的雷诺数恒大于紊流向层流转换的雷诺数。前者称上临界雷诺数，其值随试验条件而变，很不稳定；后者称下临界雷诺数，其值比较稳定，对于一般条件下的管流（圆管直径为特征长度，断面平均流速为特征速度），约为2300。 层流只存在粘滞切应力。在简单的剪切流中，粘滞切应力： 式中 为剪切变形速度,亦即速度沿垂直方向的变化率；μ为动力粘滞系数,只和液体种类及温度有关的常数。此式表达了著名的牛顿内摩擦定律。层流中摩擦阻力及沿程水头损失均与流速的一次方成正比，流速分布呈抛物线型。圆管层流流速分布如图1所示。 紊流又称湍流。液体运动呈随机性，即速度、压强等均随时间、空间作不规则的脉动，是紊流的基本特征（图2）。可采用时间平均法,将任一物理量的瞬时值分解为时均值与脉动值，即： 式中u∞、ū∞、u'分别为某一点处沿x方向的瞬时流速、时均流速与脉动流速；p、圴、p'分别为某点处的瞬时压强、时均压强与脉动压强;T为适当选取进行平均的时段。 紊流中除粘滞切应力τ1外,还有紊流附加切应力τ。由纳维－斯托克斯方程导出紊流时均运动的雷诺方程,就会增添紊流附加应力，又称雷诺应力。如紊流时均速度分量仅有ūx＝ūx(y),则有： 式中v为紊动交换系数或涡旋运动粘滞系数。和运动粘滞系数υ不同,它不是单由物性决定的常数，而是和流动状态有关的变量。 关于τ或v的计算,常用L.普朗特提出的动量传递理论，即： 式中l为混合长。显然 。按照动量传递理论结合实验,已导出紊流的对数型速度分布公式,与实验结果比较接近。与层流相比较，紊流流速分布趋于均匀，摩擦阻力和水头损失增大，在充分发展的紊流中，沿程水头损失与流速的二次方成正比。

查看详情

紊流恒定流动简介

紊流恒定流动即如果紊流流动中各物理量的时均值不随时间变化，仅仅是空间点的函数的时均流动。 是恒定流动。2100433B

查看详情

植物条件下明渠紊流拟序结构和紊流类型研究结题摘要

本研究采用圆柱棒模拟植物，利用ADV测量流场，并结合流动显示技术，对植物条件下明渠结构进行了实验研究。主要针对植物局部阻力系数、紊流统计矩、紊流特征长度（渗透深度和零平面位移）、紊流拟序结构进行了研究，发表相关文章12篇（标注论文7篇），待出版著作2部，授权发明专利2项，实用新型专利1项，获软件著作权1项，获得教育部优秀成果技术发明二等奖1项（本人排名6），协助培养博士2名、硕士1名，独立培养硕士4名，参加国内学术会议1次，国际学术会议1次，完成了项目的预期成果指标。主要的研究成果概括如下： 1、基于受力分析，提出了局部水流阻力、局部植被阻力、局部植被阻力系数的公式的形式，结合ADV流场测量结果，运用ACI分析方法，建立了植物局部阻力系数经验公式。根据植物局部阻力系数沿水深分布规律，将植物内层分为三个区域：（1）类非淹没区（局部植物阻力系数沿水深不变的区域，植物顶层的涡不能扩展到此区域，类非淹没区的上限近似为渗透深度）（2）增长区（局部植物阻力系数沿水深增大的区域）（3）减小区（局部植物阻力系数沿水深减小的区域）。研究为植物水流的精细模拟提供了依据，也为植物层内部紊流机理的研究提供了思路。 2、对断面平均流速、植物淹没度、植物密度对于紊流统计一阶、二阶、高阶矩（平均流速、紊动强度、雷诺应力、偏态系数、峰态系数）的影响进行了实验研究。实验表明，植物和水流条件对于一阶、二阶矩影响明显，对于高阶矩影响不明显。通过渗透深度的定义和雷诺应力的分布，对渗透深度进行了研究，发现淹没度和植物的刚柔度对其影响明显。根据零平面位移厚度的定义和雷诺应力分布、流速分布，计算了不同工况下的零平面位移厚的，其变化趋势和渗透深度近似。 3、运用流动显示技术（荧光钠素为示踪剂）、PIV技术和数字图像处理技术，对植物条件下明渠紊流拟序结构进行了研究。实验结果表明，植物的存在改变了明渠条件下的紊流结构，与无植物明渠存在明显差异。根据拟序结构特性，将流动划分为三个区域：植物内层区，为弱猝发现象与类卡门涡街的综合作用；植物顶部附近区，紊流结构及类型复杂，既有猝发过程，也存在自由混合层中大涡配对现象，其中猝发频率及喷射高度与淹没度及流速成正相关；植物外层区，与自由剪切紊流类似，表现为涡体拉伸及紊流的间歇性。 2100433B

查看详情

热门搜索

造价通

紊流强度

紊流强度简介

紊流强度造价信息

高强度竹基纤维墙板

高强度竹基纤维墙板

高强度竹基纤维栏杆

高强度竹基纤维栏杆

高强度竹基纤维栏杆

高强度彩色复合

高强度彩色复合

高强度彩色复合

高强度彩色复合

高强度彩色复合

立式紊流搅拌机

高强度密封索

骨骼强度

骨骼强度

骨骼强度

紊流强度常见问题

紊流强度文献

层流和紊流概述

紊流恒定流动简介

植物条件下明渠紊流拟序结构和紊流类型研究结题摘要

相关推荐