信号系统和变换
《信号系统和变换》是机械工业出版社出版的图书,作者是(美)菲利普斯。
-

选择特殊符号
选择搜索类型
请输入搜索
《信号系统和变换》是机械工业出版社出版的图书,作者是(美)菲利普斯。

译者序
前言
第1章 概述
1.1 建模
1.2 连续时间系统
1.3 采样器和离散时间系统
1.4 关于MATLAB和SIMULINK
1.5 有关信号与系统的参考文献
参考文献
第2章 连续时间信号和系统
2.1 连续时间信号变换
2.2 信号特性
2.3 常见工程信号
2.4 奇异函数
2.5 信号的数学表达式
2.6 连续时间系统
2.7 连续时间系统的性质
本章小结
参考文献
习题
第3章 连续线性时不变系统
3.1 连续时间信号的脉冲分量表示
3.2 连续时间LTI系统的卷积计算
3.3 卷积的性质
3.4 连续LTI系统的性质
3.5 微分方程的建立与求解
3.6 自由响应的分量
3.7 复指数信号作用下的系统响应
3.8 框图
本章小结
参考文献
习题
第4章 傅里叶级数
…………
出版社: 机械工业出版社; 第1版 (2006年1月1日)
丛书名: 电子与电气工程丛书
平装: 520页
开本: 16开
ISBN: 7111176189
条形码: 9787111176183
尺寸: 26 x 18.4 x 1.9 cm
重量: 762 g
接电线 接电线 接电线
随着科技的进步,地铁逐渐走进越来越多人的日常生活,要知道除了供电系统、地铁车辆、车辆段等,还有一样东西对对铁运营十分重要,那就是地铁信号系统。今天,小编就带你一起来了解一下信号系统的"三大件...
自动化 地铁上应用很多 我的理解是 不用人操作,用机器来自动运转。表现在列车的驾驶模式,以及联锁系统,少了操作,自动运转,人只需要监管就可以了。

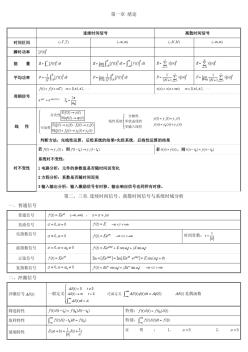 信号系统笔记傅里叶变换常用变换对信号系统常用手册
信号系统笔记傅里叶变换常用变换对信号系统常用手册
信号系统笔记傅里叶变换常用变换对信号系统常用手册
信号系统笔记傅里叶变换常用变换对信号系统常用手册

 地铁信号系统中的智能信号功能分析
地铁信号系统中的智能信号功能分析
地铁信号系统中的智能信号功能分析
随着城市化的不断发展,城市地面交通压力增大,地铁工程的发展能够实现对交通压力的有效缓解.在其发展过程中,地铁信号系统的发展,能够促进其自动运行、控制、防护以及报警.随着现代地铁信号技术的发展以及信息技术的深入,地铁信号系统向着智能化发展.对于地铁信号系统而言,需要结合当前信息与通信技术的发展,加快自动化和智能化发展的速度,在根本上保证地铁的高效运行,提高安全系数.鉴于此,本文主要分析地铁信号系统中的智能信号功能.
离散余弦变换(DCT for Discrete Cosine Transform)是与傅里叶变换相关的一种变换,它类似于离散傅里叶变换(DFT for Discrete Fourier Transform),但是只使用实数。离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,这个离散傅里叶变换是对一个实偶函数进行的(因为一个实偶函数的傅里叶变换仍然是一个实偶函数),在有些变形里面需要将输入或者输出的位置移动半个单位(DCT有8种标准类型,其中4种是常见的)。
最常用的一种离散余弦变换的类型是下面给出的第二种类型,通常我们所说的离散余弦变换指的就是这种。它的逆,也就是下面给出的第三种类型,通常相应的被称为"反离散余弦变换","逆离散余弦变换"或者"IDCT"。
有两个相关的变换,一个是离散正弦变换(DST for Discrete Sine Transform),它相当于一个长度大概是它两倍的实奇函数的离散傅里叶变换;另一个是改进的离散余弦变换(MDCT for Modified Discrete Cosine Transform),它相当于对交叠的数据进行离散余弦变换。
离散余弦变换,尤其是它的第二种类型,经常被信号处理和图像处理使用,用于对信号和图像(包括静止图像和运动图像)进行有损数据压缩。这是由于离散余弦变换具有很强的"能量集中"特性:大多数的自然信号(包括声音和图像)的能量都集中在离散余弦变换后的低频部分,而且当信号具有接近马尔科夫过程(Markov processes)的统计特性时,离散余弦变换的去相关性接近于K-L变换(Karhunen-Loève 变换--它具有最优的去相关性)的性能。
例如,在静止图像编码标准JPEG中,在运动图像编码标准MJPEG和MPEG的各个标准中都使用了离散余弦变换。在这些标准制中都使用了二维的第二种类型离散余弦变换,并将结果进行量化之后进行熵编码。这时对应第二种类型离散余弦变换中的n通常是8,并用该公式对每个8x8块的每行进行变换,然后每列进行变换。得到的是一个8x8的变换系数矩阵。其中(0,0)位置的元素就是直流分量,矩阵中的其他元素根据其位置表示不同频率的交流分量。
一个类似的变换, 改进的离散余弦变换被用在高级音频编码(AAC for Advanced Audio Coding),Vorbis 和 MP3 音频压缩当中。
离散余弦变换也经常被用来使用谱方法来解偏微分方程,这时候离散余弦变换的不同的变量对应着数组两端不同的奇/偶边界条件。
离散余弦变换被广泛的应用,像是资料压缩、特征萃取、影像重建等等。多维度离散余弦变换为:
其中一个常用的多维度变换就是傅立叶变换,是将一个讯号的表示式从时域/空域转换到频域。 离散域的多维度傅立叶变换可表示成下列式子:
快速傅立叶变换(FFT)是一种用来计算离散傅立叶变换(DFT)和其逆变换的快速算法,快速傅立叶变换所得到的结果跟按照定义去算离散傅立叶变换的结果是一样的,但唯一的差别是快速傅立叶变换的速度快很多。(在舍入误差的存在下,很多快速傅立叶变换还比直接照定义算还更精准。)有很多种快速傅立叶变换,他们包含很广泛的数学运算,从简单的复数运算到数论和群论,详情可以看快速傅立叶变换。
多维度的离散傅立叶变换是离散域傅立叶变换的简单版本,其方法是在均匀间隔下的样本频率去估计其值 .
逆多维DFT方程是: