选择特殊符号

Ф δ ° × # Ⅱ Ⅲ ½ ¼

选择搜索类型

市场价信息价参考价询价供应商云知资讯文库百科

热门搜索

造价通

请输入搜索

首页 > 百科 > 建设工程百科

样本统计量

样本统计量（简称统计量）指的是样本的函数，并且此函数不含有未知参数。常见的统计量有：样本均值，样本方差，样本极差等。

样本统计量基本信息

中文名样本统计量
外文名sample statistics
简称统计量
概述样本的函数
举例样本均值，样本方差
应用领域统计学

样本统计量举例

例1 设X₁,X₂,...,X_n为总体X的样本，其容量为n. 记 则 及 都是统计量，称 及 分别为样本X₁,X₂,...,Xn的平均值及方差。样本的观察值为x₁,x₂,...,x_n， 及 的观察值分别记作

样本统计量造价信息

市场价
信息价
询价

能源计量监测软件

规格型号：
BEMS 8.0
价格行情：
材料单位：
套
材料品牌：
荣夏
材料税率：
13%
供应商：
江苏荣夏安全科技有限公司
报价时间：
2022-12-07

查看价格

计量用二次电缆

规格型号：
KVVP22-10×4mm2
价格行情：
材料单位：
m
材料品牌：
小猫
材料税率：
13%
供应商：
天津市电缆总厂橡塑电缆厂
报价时间：
2022-12-07

查看价格

客流量统计设备

规格型号：
1.工作电压/电流:DC6V/0.5A2.工作功率:≤2.5W3.待机功耗:≤1.5w4.功能描述:当有人于男页或女如如厕时,人流量统计探头将会自动计数海康威视
价格行情：
材料单位：
个
材料品牌：
材料税率：
13%
供应商：
深圳市光明源智能科技有限公司
报价时间：
2022-12-07

查看价格

客流统计服务器

规格型号：
品种:客流统计服务器;参数说明:客流统计服务器,描述:iVMS-6200E-C(公司智能专用服务器硬件),描述:接入标准H.264码流,不区
价格行情：
材料单位：
个
材料品牌：
海康威视
材料税率：
13%
供应商：
杭州护家科技有限公司
报价时间：
2022-12-07

查看价格

客流统计服务器

规格型号：
品种:客流统计服务器;参数说明:客流统计服务器,描述:iVMS-6200E-C(公司智能专用服务器硬件),描述:接入标准H.264码流,不区
价格行情：
材料单位：
个
材料品牌：
海康威视
材料税率：
13%
供应商：
杭州护家科技有限公司
报价时间：
2022-12-07

查看价格

计量柜

规格型号：
800KVA-SSL600×2200×1000
价格行情：
材料单位：
套
材料税率：
地区时间：
惠州市2018年3月信息价
所属行业：
建筑工程
备注说明：

查看价格

计量柜

规格型号：
630KVA-SSL600×2200×1000
价格行情：
材料单位：
套
材料税率：
地区时间：
惠州市2018年2月信息价
所属行业：
建筑工程
备注说明：

查看价格

计量柜

规格型号：
500KVA-SSL600×2200×1000
价格行情：
材料单位：
套
材料税率：
地区时间：
惠州市2018年2月信息价
所属行业：
建筑工程
备注说明：

查看价格

计量柜

规格型号：
1000KVA-SSL600×2200×1000
价格行情：
材料单位：
套
材料税率：
地区时间：
惠州市2018年1月信息价
所属行业：
建筑工程
备注说明：

查看价格

计量柜

规格型号：
800KVA-SSL600×2200×1000
价格行情：
材料单位：
套
材料税率：
地区时间：
惠州市2017年10月信息价
所属行业：
建筑工程
备注说明：

查看价格

生物样本

规格型号：
1、支持对有关的样本等进行记录.2、支持样本入库,出库去向的追踪.
需求量：
1人日
报价数：
1
材料品牌：
材料档次：
中高档
费用说明：
含税费 | 含运费
询价时间：
2022-08-23

查看价格

样本制备间台

规格型号：
样本制备间台
需求量：
1m
报价数：
1
材料品牌：
材料档次：
中高档
费用说明：
含税费 | 含运费
询价时间：
2021-11-05

查看价格

称重系统计量标定

规格型号：
包括整车称台安装后首次验收检测和缺陷责任期内所必须的检测
需求量：
8台
报价数：
1
材料品牌：
山西国强
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2020-11-10

查看价格

陶瓷样本

规格型号：
中国各大名窑实物(仿)十四件及简介,可陈设、展示、欣赏.官、哥、汝、均、定窑仿制品各1件、釉下青花瓷仿制品、泥条成型、泥板成型、拉坯成型作品各1件、新石器时期文物仿制品3件、唐三彩作品1件、宜兴紫砂陶壶1件
需求量：
1套
报价数：
3
材料品牌：
天智、神州、宏博
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2020-07-20

查看价格

计量点1:双向计量装置

规格型号：
计量点1:双向计量装置
需求量：
1套
报价数：
3
材料品牌：
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2022-11-23

查看价格

样本统计量拓展

样本统计量顺序统计量 定义3 设X₁,X₂,...,X_n为总体X的样本，今由样本建立n个函数： 其中 为这样的统计量，它的观察值为 ， 为样本X₁,X₂,...,X_n的观察值x₁,x₂,...,x_n中由小到大排列后的第k为数值，则称 为顺序统计量。 注：易见， 称 为最小项统计量， 为最大项统计量。 样本统计量极差 定义4 设X₁,X₂,...,X_n为总体X的样本，则称统计量 为样本的极差。 注：极差是样本中最大值与最小值之差，反映了样本观察值的波动幅度。它同方差一样是反映观察值离散程度的数量指标，而且计算方便。 样本统计量抽样分布 统计量是对总体X的分布函数或数字特征进行估计与推断最重要的基本概念，求出统计量T(x₁,x₂,...,x_n)的分布函数是数理统计学的基本问题之一。统计量的分布，称为抽样分布。 2100433B

样本统计量定义

样本统计量简单随机样本 定义1 设X₁,X₂,...,X_n是来自总体X的容量为n的样本，如果X₁,X₂,...,X_n相互独立且每一个都是与总体X有相同分布的随机变量，则称X₁,X₂,...,X_n为总体X的容量为n的简单随机样本，简称为简单样本或样本。 注：样本X₁,X₂,...,X_n也可用n维随机向量 (X₁,X₂,...,X_n) 表示。记x_i为X_i的一次观察值，并称(x₁,x₂,...,x_n)为样本X₁,X₂,...,X_n的一次观察值。 样本统计量样本统计量 定义2 设X₁,X₂,...,X_n为总体X的样本，T为n维实值函数，作样本X₁,X₂,...,X_n的函数T=T(X₁,X₂,...,X_n)（不带未知参数的随机变量），T的取值记为t=T(x₁,x₂,...,x_n)，称T或T(X₁,X₂,...,X_n)为样本统计量，简称为统计量。 注：1）统计量指的是样本的函数，并且不含有未知参数。样本的函数等价于定义在样本空间上的函数。 2）给定样本的一次观察值x=(x₁,x₂,...,x_n) 时，T(x₁,x₂,...,x_n)的值完全确定。

样本统计量常见问题

成本分析样本

给你发一个，你根据实际情况修改一下啊！
投标书的封面样本和外包装样本

你制作标书时，那个没有要求吗？
企化书样本

　　?这是一个可以提供写项目计划的样本,很实用.希望可以给你的工作带来方便. 　　项目计划　　序号：　　项目名称：　　执行部门：负责人：　　项目类别：　　[ ] 软科学研究项目 [ ] 科...

样本统计量文献

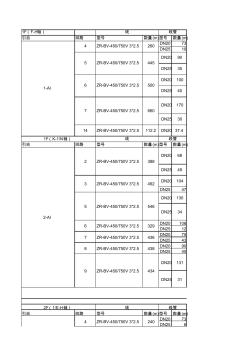照明统计量

照明统计量

照明统计量

格式：pdf

大小：180KB

页数： 12页

1F（F-H轴）引自回路型号数量 (m)型号数量 (m) DN20 73 DN25 10 引自回路型号数量 (m)型号数量 (m) DN25 47 DN20 106 DN25 12 DN20 75 DN25 43 DN20 90 DN25 40 引自回路型号数量 (m)型号数量 (m) DN20 73 DN25 6 436 2F（1/E-H轴）线线管 9 2-Al ZR-BV-450/750V 3*2.5 434 DN20 37.4 2 ZR-BV-450/750V 3*2.5 388 DN20 68 1F（K-1/N轴）线线管 DN25 49 1-Al 6 ZR-BV-450/750V 3*2.5 500 DN20 100 DN25 40 7 ZR-BV-450/750V 3*2.5 660 DN20 170 8 ZR-BV-450/750V 3*2.5

在线阅读立即下载

双桥静力触探分层统计表样本

双桥静力触探分层统计表样本

双桥静力触探分层统计表样本

格式：pdf

大小：180KB

页数： 3页

第 1 页层号统计项目 qc(MPa) qc(MPa) qc(MPa) qc(MPa) qc(MPa) 最小值 0.832 1.764 0.474 1.506 7.560 最大值 1.877 3.211 0.786 2.306 10.858 数据个数n 52 52 52 40 42 厚度加权平均值 1.295 2.442 0.618 1.902 9.096 标准差 σ 0.713 0.614 0.124 0.328 1.284 变异系数 δ 0.55 0.25 0.20 0.17 0.14 标准值 1.125 2.296 0.589 1.812 8.755 最小平均值 1.063 2.103 0.546 1.704 8.328 层号孔号 qc(MPa) fs(KPa) 厚度(m) qc(MPa) fs(KPa) 厚度(m) qc(MPa) f

在线阅读立即下载

统计量统计量

统计量样本矩 设x1,x2，…，xn是一个大小为n的样本，对自然数k，分别称为k阶样本原 点矩和k阶样本中心矩，统称为样本矩。许多最常用的统计量，都可由样本矩构造。例如，样本均值（即α1）和样本方差是常用的两个统计量，前者反映总体中心位置的信息，后者反映总体分散情况。还有其他常用的统计量，如样本标准差，样本变异系数S/塣，样本偏度，样本峰度等都是样本矩的函数。若(x1,Y1），（x2,Y2），…，（xn,Yn）是从二维总体（x，Y）抽出的简单样本，则样本协方差·及样本相关系数也是常用的统计量，r可用于推断x和Y的相关性。 统计量次序统计量 把样本X1,x2，…，xn由小到大排列，得到，称之为样本x1,x2，… ,xn的次序统计量。其中最小次序统计量x⑴最大次序统计量x(n）称为极值，在那些如年枯水量、年最大地震级数、材料的断裂强度等的统计问题中很有用。还有一些由次序统计量派生出来的有用的统计量，如：样本中位数是总体分布中心位置的一种度量，若样本大小n为奇数，，若n为偶数，，它容易计算且有良好的稳健性。样本p分位数Zp(0<p<1）及极差x(n)-x⑴也是重要的统计量。其中Zp当时即为中位数，而当时，表示不超过1 np的最大整数）。样本分位数的一个重要应用是构造连续总体分布的非参数性容忍区间（见区间估计）。 统计量U统计量 这是W.霍夫丁于1948年引进的，它在非参数统计中有广泛的应用。其定义是：设x1,x2，…，xn，为简单样本，m为不超过n的自然数，为m元对称函数，则称为样本x1,x2，…，xn的以为核的U统计量。样本均值和样本方差都是它的特例。从霍夫丁开始，这种统计量的大样本性质得到了深入的研究，主要应用于构造非参数性的量的一致最小方差无偏估计（见点估计），并在这种估计的基础上检验非参数性总体中的有关假设。 统计量秩统计量 把样本X1，X2，…，Xn 按大小排列为，若则称Ri为xi的秩，全部n个秩R1，R2，…，Rn构成秩统计量，它的取值总是1,2，…，n的某个排列。秩统计量是非参数统计的一个主要工具。 还有一些统计量是因其与一定的统计方法的联系而引进的。如假设检验中的似然比原则所导致的似然比统计量，K.皮尔森的拟合优度（见假设检验）准则所导致的Ⅹ统计量，线性统计模型中的最小二乘法所导致的一系列线性与二次型统计量，等等。

斑砂岩统简介

斑砂岩统（Buntsandsteinian Series）是德国陆相下三叠统的专名。斑砂岩统是以岩性取名。它为大陆或潟湖相沉积，岩性主要为红色或淡紫色砾岩、砂岩或页岩。上部出现海相沉积，含有双壳类Myophoria等。

统威品牌简介

统威致力于打造优质产品、不断追求创新，力求给人们带来更舒适更优质的生活便捷！ 品牌注册地址：湖北省武汉市洪山区雄楚大道杨家湾549号尚文创业城2-1-1005室 品牌线：统威

相关推荐

相关百科
相关知识
相关专栏

免费服务热线: 400-888-9639