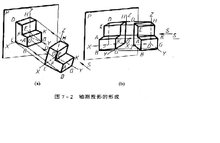
轴测投影的形成
将物体连同其直角坐标体系,沿不平行与任一坐标平面的方向,用平行投影法将其投射在单一投影面上所得到的图形,称为轴测投影(轴测图),如图7-2a 、b中投影P上所得到的图形。
轴测投影被选定的单一投影P,称为轴测投影面。直角坐标轴OX、OY、OZ在轴测投影P上的轴测投影OX、OY、OZ,称为轴测投影轴,简称轴测轴。
直角坐标体系 由三根相互垂直的轴(直角坐标轴)和相同的原点及其计量单位所构成的坐标体系。
坐标体系 确定空间每个点及其相应位置之间关系的基准体系。
直角坐标轴 在直角体系中垂直相交的坐标轴。
坐标平面 任意两根坐标轴所确定的平面。
原点 坐标轴的基准点。
轴测投影也属于平行投影,且只有一个投影面。当确定物体的三个坐标平面不与投射方向一致时,则物体上平行于三个坐标平面的平面图形的轴测投影,在轴测投影面上都得到反映,因此,物体的轴测投影才有较强的立体感。
轴测投影(轴测图)通常不画不可见轮廓的投影(虚线)。
轴间角和轴向伸缩系数
1.轴间角
轴测投影中任意两根直角坐标轴在轴测投影面上的投影之间的夹角,称为轴间角。如图5-2所示,两轴侧轴之间夹角(∠XOY、∠XOZ、∠YOZ),用它来控制轴测投影的形状变化。
2. 轴向伸缩系数
直角坐标轴的轴测投影的单位长度,与相应直角坐标轴上的单位长度的比值,称为轴向伸缩系数,如图所示,其中,用p表OX轴轴向伸缩系数,q表示OY轴轴向伸缩系数,r表示OZ轴轴向伸缩系数,用轴向伸缩系数控制轴测投影的大小变化。
轴测投影的基本性质
轴测投影同样具有平行投影的性质:
(1)若空间两直线段相互平行,则其轴测投影相互平行。
(2)凡与直角坐标轴平行的直线段,其轴测投影必平行于相应的轴测轴,且其伸缩系数于相应轴测轴的轴向伸缩系数相同。因此,画轴测投影时,必沿轴测轴或平行于轴测轴的方向才可以度量。轴测投影因此而得名。
(3)直线段上两线段长度之比,等于其轴测投影长度之比。
轴测投影的分类
按获得轴测投影的投射方向对轴测投影面的相对位置不同,轴测投影可分为两大类:
1.正轴测投影
用正投影法得到的轴测投影,称为正轴测投影。
2.斜轴测投影
用斜投影法得到的轴测投影,称为斜轴测投影。
由于确定空间物体位置的直角坐标轴对轴测投影面的倾角大小不同,轴向伸缩系数也随之不同,故上述两类轴测投影又个分为三种:
正轴测投影分为:
(1)正等轴测投影(正等轴测图)
三个轴向伸缩系数均相等(p= q=r)的正轴测投影,称为正等轴测投影(简称正等测)。
(2)正二等轴测投影(正二轴测图)
两个轴向伸缩系数相等(p=q≠r或p=r≠q或q=r≠p)的正轴测投影,称为正二等轴测投影(简称正二测)。
(3)正三轴测投影(正三轴测图)。
三个轴向伸缩系数均不相等(p≠q≠r)的正轴测投影,称为正三轴测投影(简称正三测)。
斜轴测投影分为:
(1)斜等轴测投影(斜等轴测图)
三个轴向伸缩系数均相等(p=q=r)的斜轴测投影,称为斜等轴测投影(简称斜等测)。
(2)斜二等轴测投影(斜二轴测图)
轴测投影面平行一个坐标平面,且平行于坐标平面的两根轴的轴向伸缩系数相等(p=q≠r或p=r≠q 或q=r≠p)的斜轴测投影,称为斜二等轴测投影(简称斜二测)。
(3)斜三轴测投影(斜三轴测图)
三个轴向伸缩系数均不等(p≠q≠r)的斜轴测投影,称为斜三轴测投影(简称斜三测)。
在实际工作中,正等测、斜二等测用得交多,正(斜)三测的作图较繁,很少采用。本章只介绍正等测和斜二测的画法。
-