选择特殊符号

Ф δ ° × # Ⅱ Ⅲ ½ ¼

选择搜索类型

市场价信息价参考价询价供应商云知资讯文库百科

热门搜索

造价通

请输入搜索

首页 > 百科 > 建设工程百科

中位线定理

中位线是在三角形或梯形中一条特殊的线段，与其所在的三角形或梯形有着特殊的关系。连接三角形的两边中点的线段叫做三角形的中位线。三角形有三条中位线，首尾相接时，每个小三角形面积都等于原三角形的四分之一，这四个三角形都互相全等。

中位线定理基本信息

中文名称中位线定理
外文名称Median line of triangle
用途平面几何线段间的关系

中位线定理造价信息

市场价
信息价
询价

车位线

规格型号：
品种:车位线
价格行情：
材料单位：
组
材料品牌：
路畅
材料税率：
13%
供应商：
南京润畅交通科技有限公司
报价时间：
2022-12-06

查看价格

车位线

规格型号：
品种:车位线
价格行情：
材料单位：
组
材料品牌：
路畅
材料税率：
13%
供应商：
天津鑫天亚道路设施贸易有限公司
报价时间：
2022-12-06

查看价格

车位线

规格型号：
品种:车位线;型号:实际车型;
价格行情：
材料单位：
个
材料品牌：
益恒
材料税率：
13%
供应商：
安徽益恒交通设施工程有限公司
报价时间：
2022-12-06

查看价格

车位线

规格型号：
品种:车位线,规格型号:6000×2500mm,材质:冷漆
价格行情：
材料单位：
个
材料品牌：
空灵
材料税率：
13%
供应商：
杭州隆全交通设施工程有限公司
报价时间：
2022-12-06

查看价格

车位线

规格型号：
品种:车位线;规格(mm):线宽120;
价格行情：
材料单位：
个
材料品牌：
天恒
材料税率：
13%
供应商：
西安天恒交通设施有限公司
报价时间：
2022-12-06

查看价格

导线卷车

规格型号：
DSJ23-122
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2012年4季度信息价
所属行业：
建筑工程
备注说明：

查看价格

导线卷车

规格型号：
DSJ23-122
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2012年3季度信息价
所属行业：
建筑工程
备注说明：

查看价格

导线卷车

规格型号：
DSJ23-122
价格行情：
材料单位：
台班
材料税率：
地区时间：
广州市2011年1季度信息价
所属行业：
建筑工程
备注说明：

查看价格

导线卷车

规格型号：
DSJ23-122
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2010年1季度信息价
所属行业：
建筑工程
备注说明：

查看价格

导线卷车

规格型号：
DSJ23-122
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2009年2季度信息价
所属行业：
建筑工程
备注说明：

查看价格

勾股定理

规格型号：
1200×800×1200
需求量：
1项
报价数：
3
材料品牌：
材料档次：
中档
费用说明：
含税费 | 不含运费
询价时间：
2022-09-21

查看价格

四色定理

规格型号：
1200×800×1200
需求量：
1项
报价数：
3
材料品牌：
材料档次：
中档
费用说明：
含税费 | 不含运费
询价时间：
2022-09-21

查看价格

车位线

规格型号：
实际车型
需求量：
470个
报价数：
1
材料品牌：
材料档次：
中高档
费用说明：
含税费 | 含运费
询价时间：
2021-12-29

查看价格

车位线

规格型号：
环氧冷涂:环氧树脂漆(二遍)
需求量：
3043m²
报价数：
3
材料品牌：
材料档次：
中档
费用说明：
不含税费 | 不含运费
询价时间：
2021-10-23

查看价格

车位线

规格型号：
实际车型
需求量：
566个
报价数：
3
材料品牌：
不限，推荐三家，简图详见附件，含税费、运费及安装费
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2021-07-15

查看价格

中位线定理常见问题

什么是梯形中位线

看书
梯形的中位线怎么计算

梯形的中位线就是上底与下底的和的一半
梯形的中位线的一些判定方法

中位线定理文献

巧用“中位线”,构架解题桥梁

巧用“中位线”,构架解题桥梁

巧用“中位线”,构架解题桥梁

格式：pdf

大小：167KB

页数： 2页

三角形＂中位线＂的性质定理在几何求解题中的应用比较广泛,中考常考.在大多数题目中,＂中位线＂的组成,大多不是完整地表现出来,需要我们在解题时,能够抓住题目中的已知信息,补全三角形＂中位线＂的残缺部分,以此作为添加辅助的方法,构造解题桥梁,从而达到快速解题.下面试举几例,以示说明.

在线阅读立即下载

巧用“ 中位线”,构架解题桥梁

巧用“ 中位线”,构架解题桥梁

巧用“ 中位线”,构架解题桥梁

格式：pdf

大小：167KB

页数： 2页

三角形“中位线”的性质定理在几何求解题中的应用比较广泛,中考常考.在大多数题目中,“中位线”的组成,大多不是完整地表现出来,需要我们在解题时,能够抓住题目中的已知信息,补全三角形“中位线”的残缺部分,以此作为添加辅助的方法,构造解题桥梁,从而达到快速解题.下面试举几例,以示说明.

在线阅读立即下载

梯形中位线定理定理定义

梯形的中位线等于梯形的上底加下底再除以二，用符号表示是L. L=(a+b)÷2 已知中位线长度和高，就能求出梯形的面积. S梯=2Lh÷2=Lh 中位线在关于梯形的各种题型中都是一条得天独厚的辅助线。

梯形中位线定理验证推导

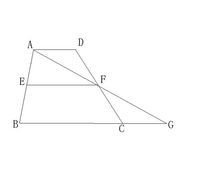
如图，四边形ABCD是梯形，AD∥BC，E、F分别是AB、CD边上的中点，求证:EF∥AD，且EF=(AD+BC)/2 证明: 连接AF并延长交BC的延长线于G。 ∵AD∥BC ∴∠ADF=∠GCF ∵F是CD的中点 ∴DF=FC ∵∠AFD=∠CFG ∴△ADF≌△GCF(ASA) ∴AF=FG，AD=CG ∴F是AG的中点 ∵E是AB的中点 ∴EF是△ABG的中位线 ∴EF∥BG,EF=BG/2=(BC+CG)/2 ∴EF=(AD+BC)/2 ∵AD∥BC ∴EF∥AD∥BC

梯形中位线定理特例做法

如图的梯子。已知梯子每跨一步上升高度 相同，则求内部横杆总长。 题示(做这些题目要注意题目的细节--上升高度相同，即每条横杆都是小梯形的中位线) 如果同学没有掌握技巧，只会死算，那么大多只能做如图的最左的五步梯，可以设未知数解，时间消耗很大，尤其是运气不佳遇到中间或右边的多步梯，X、Y、Z算的都要吐血了。 但是题目做多了，我总结了一个规律，以左图五步梯为例:五根横杆的总长为1/2(30cm+50cm)X5 中图七步梯为例:1/2(40cm+60cm)X7 那么同理，右图九步梯则是1/2(50cm+70cm)X9 总结一下就是1/2(上底+下底)Xn

相关推荐

相关百科
相关知识
相关专栏

免费服务热线: 400-888-9639