严谨的工作作风、对技术精益求精的精神、对工作极端负责的态度是减少装配误差的思想基础，在具体操作中，还有下列几种直接减少装配误差的方法需要注意。
一、选择合理的装配基准
为了使零件装配位置准确，选择已经定位的零件的某一部位(点、线、面)，作为待装零件的定位依据，这个部位就叫做装配基准。装配基准的正确选择，是提高装配精度，减少装配误差的重要因素，必须认真对待。正确选择装配基准，一般应考虑下列因素。
(1)尽量选择零件加工精度较高的部位，即尺寸公差小、形状精度高、位置偏差小、粗糙度低的部位作为基准。如罗拉制造时的沟槽部分直径公差和径向跳动比光面部位低，因此在检查罗拉弯曲、校正罗拉隔距时，都以沟槽部位为基准。
(2)基准部位尽量靠近装配调节点，如平车面时，依靠车架升降螺钉调节车面高低，所以平尺搁铁要尽可能放在靠车架部位。如把平尺搁铁放在离车架较远的地方，使基准点远离车架，当调节邻近车架高低时，会带动这一搁铁升降，使基准漂移。如图1所示，设两车架的中心距AB为1008mm，A点为车面顶面已调平的一点，B点为车面顶面打算调平的一点。平尺搁铁应放在A点最为合理，如不放在A处而放在D处，离A点100mm(AD)，当校正车面长向水平时，调节点处的车面从B点调到C点，调高0.10mm(BC)，这一平尺搁铁也被带动由D点升至E点，上升0.01mm(DE)，即基准被抬高0.01mm。
由此说明，平尺搁铁离车架愈远时，基准面的高低变化愈大，影响装配精度。
(3)尽量重复使用同一基准，排除零件表面形状偏差。如:由于顶面存在着一定程度的长向弯曲和宽向扭曲，因此，要将看车面长向水平的平尺搁铁、看车面宽向水平的水平仪和托前罗拉高低线的托线圆辊，放在同一部位，避免由于车面顶面不平带来的附加误差。
(4)选择基准时还应考虑平装操作方便的因素。如锭轴斜齿轮左右定位，一般有两种方法:一种是插上锭子，以锭子为基准，用卡板定位;另一种是不插锭子，以下龙筋油杯为基准。虽然锭子直径公差比油杯孔公差小，但插上锭子后定位增加困难。而以油杯孔为基准，能满足锭轴齿轮左右定位要求，可不插锭子，使操作方便。
(5)尽量和机械制造厂零件加工和预装配的基准部位一致起来。
二、避免装配基准的多次传递(减少累计误差)
要把1m长的直线分为十等分有以下两种方法:一种是用150mm的钢直尺，每量1OOmm移动一次钢直尺，共量十次;另一种是用1m长的钢直尺，不移动，而按相对应的刻度线依次取十个点。显然后一种方法的误差比较小。因为前一种方法，由于测量基准的多次移动，使两个和两个以上的装配误差(工具、操作误差)叠加在一起，就产生了累计误差。同样道理，当用规定度的塞尺测量间隙时，应尽可能选用单页的塞尺测量比较准确，而避免使用二页或更多的薄塞尺叠起来测量。
三、掌握误差的变化规律(消除系统误差)
如果发现了误差的变化规律，查明了数值，就如以在装配中设法消除这一误差值，这种有规律性的误差，叫做系统误差。如当一把游标卡尺的内径量爪磨灭0.02mm，使每次测量的读数虚大0.02mm，就可以把读数主动减去0.02mm，得到需要的真实读数。又如当水平仪气泡不准，经过定位调头检查，发现气泡不准，经过定位向某一端偏一格，才是水平状态，因此，在看水平时，应故意让主气泡向某端偏一格，使零件达到水平状态。
四、合理分配或调节误差数值(减少装配误差)
1.互借法
并条机车面、底板、粗纱机头尾墙板、车架、车面等大型铸件发生扭曲变形时，由于矫形不便，只能检查多点铅直度或水平度，使平装后的读数正反方向最大值相等，或使正反方向的最大值相减后的差值不大于允差，这种方法叫做互借法。
2.调节法
装配中累计误差超过允差时，可以把其中一个环节的尺寸、形状或加以改变，或把一个不重要的尺寸放弃，不予控制，使总尺寸在允许范围内。这个可以改变的环节叫做"调节环"，例如校并条机罗拉座开档，先从车头外侧线决定车上墙板左右位置，再以车头上墙板为基准定第一罗拉座位置，再依次定第二、第三、第四罗拉座位置，而对第四罗拉座至车尾上墙板间的尺寸就只能放弃，不可能校正，在实际工作中，调节环尺寸、形状或位置的改变，往往通过锉、垫、焊的方法来达到，或用可调节的零件来调节，如调节螺钉、调节垫圈、车脚垫板等，利用这些零件来调节可以提高装配的准确性，节省手工锉修等工作。
3.选择装配法
为了减小装配误差，提高零件装配准确性，还可以将具有一定误差的零件，通过选择，进行配套或分组，使零件之间的上下误差配合适当提高精度，叫选择装配。例如把胶辊芯子和铁壳分组配套，使间隙一致;把胶辊直径分成几档，使同台或同区机器的胶辊直径一致。
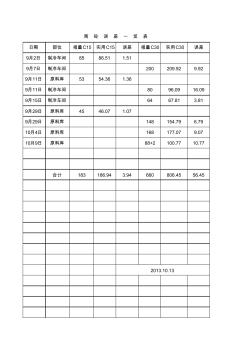商砼误差
木质门合页装配孔槽数控加工精度的热变形误差补偿方法研究
理论误差误差