最小费用最大流算法举例文献

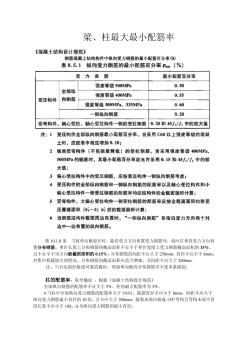 梁、柱最大最小配筋率
梁、柱最大最小配筋率
梁、柱最大最小配筋率
梁、柱最大最小配筋率
选择特殊符号
选择搜索类型
请输入搜索
augmentpath
译为“增广路”算法,其思想大致如下:
原有网络为G,设有一辅助图G',其定义为V(G') = V(G),E(G')初始值(也就是容量)与E(G)相同。每次操作时从Source点搜索出一条到Sink点的路径,然后将该路径上所有的容量减去该路径上容量的最小值,然后对路径上每一条边;添加或扩大反方向的容量,大小就是刚才减去的容量。一直到没有路为止。此时辅助图上的正向流就是最大流。
我们很容易觉得这个算法会陷入死循环,但事实上不是这样的。我们只需要注意到每次网络中由Source到Sink的流都增加了,若容量都是整数,则这个算法必然会结束。
寻找通路的时候可以用DFS,BFS最短路等算法。就这两者来说,BFS要比DFS快得多,但是编码量也会相应上增加。
增广路方法可以解决最大流问题,然而它有一个不可避免的缺陷,就是在极端情况下每次只能将流扩大1(假设容量、流为整数),这样会造成性能上的很大问题,解决这个问题有一个复杂得多的算法,就是预推进算法。
pushlabel
译为“预流推进”算法。
可以想象在一个自来水管网的源头尽可能多的注入水流之后,最多有多少水可以流到汇点去,由网络的各个节点和管道来约束流量。将每个节点都看成一个水站,他的通过能力是有限的不能通过的水只能退回去。
Push-Relabel
译为压入与重标记算法
除了用各种方法在剩余网络中不断找增广路(augmenting)的Ford-Fulkerson系的算法外,还有一种求最大流的算法被称为压入与重标记(Push-Relabel)算法。它的基本操作有:压入,作用于一条边,将边的始点的预流尽可能多的压向终点;重标记,作用于一个点,将它的高度(也就是label)设为所有邻接点的高度的最小值加一。Push-Relabel系的算法普遍要比Ford-Fulkerson系的算法快,但是缺点是相对难以理解。
Relabel-to-Front使用一个链表保存溢出顶点,用Discharge操作不断使溢出顶点不再溢出。
Discharge的操作过程是:若找不到可被压入的临边,则重标记,否则对临边压入,直至点不再溢出。
算法的主过程是:首先将源点出发的所有边充满,然后将除源和汇外的所有顶点保存在一个链表里,从链表头开始进行Discharge,如果完成后顶点的高度有所增加,则将这个顶点置于链表的头部,对下一个顶点开始Discharge。
Relabel-to-Front算法的时间复杂度是O(V^3),还有一个叫Highest Label Preflow Push的算法复杂度据说是O(V^2*E^0.5)。我研究了一下HLPP,感觉它和Relabel-to-Front本质上没有区别,因为Relabel-to-Front每次前移的都是高度最高的顶点,所以也相当于每次选择最高的标号进行更新。还有一个感觉也会很好实现的算法是使用队列维护溢出顶点,每次对pop出来的顶点discharge,出现了新的溢出顶点时入队。
Push-Relabel类的算法有一个名为gap heuristic的优化,就是当存在一个整数0k的顶点v做更新,若它小于V 1就置为V 1。
c 程序举例
typedef pair
struct edge { int to,cap,cost,rev; };
int V;
vector
int h[MAX_V];
int dist[MAX_V];
int prevv[MAX_V],preve[MAX_V];
void add_edge(int from,int to,int cap,int cost) {
G[from].push_back((edge){to,cap,cost,G[to].size()});
G[to].push_back((edge){from,0,-cost,G[from].size()-1});
}
int min_cost_flow(int s,int t,int f) {
int res;
fill(h,h V,0);
while(f>0) {
priority_queue
> que; fill(dist,dist V,INF); dist[s]=0; que.push(P(0,s)); while(!que.empty()) { P p=que.top();que.pop(); int v=p.second; if(dist[v]
if(e.cap>0&&dist[e.to]>dist[v] e.cost h[v]-h[e.to]) { dist[e.to]=dist[v] e.cost h[v]-h[e.to]; prevv[e.to]=v; preve[e.to]=i; que.push(P(dist[e.to],e.to)); } } } if(dist[t]==INF) return -1; for(int v=0;v
for(int v=t;v!=s;v=prevv[v]) d=min(d,G[prevv[v]][preve[v]].cap); f-=d; res =d*h[t]; for(int v=t;v!=s;v=prevv[v]) { edge &e=G[prevv[v]][preve[v]]; e.cap-=d; G[v][e.rev].cap =d; } } return res; }2100433B
解决最小费用最大流问题,一般有两条途径。一条途径是先用最大流算法算出最大流,然后根据边费用,检查是否有可能在流量平衡的前提下通过调整边流量,使总费用得以减少?只要有这个可能,就进行这样的调整。调整后,得到一个新的最大流。
然后,在这个新流的基础上继续检查,调整。这样迭代下去,直至无调整可能,便得到最小费用最大流。这一思路的特点是保持问题的可行性(始终保持最大流),向最优推进。另一条解决途径和前面介绍的最大流算法思路相类似,一般首先给出零流作为初始流。这个流的费用为零,当然是最小费用的。然后寻找一条源点至汇点的增流链,但要求这条增流链必须是所有增流链中费用最小的一条。如果能找出增流链,则在增流链上增流,得出新流。将这个流做为初始流看待,继续寻找增流链增流。这样迭代下去,直至找不出增流链,这时的流即为最小费用最大流。这一算法思路的特点是保持解的最优性(每次得到的新流都是费用最小的流),而逐渐向可行解靠近(直至最大流时才是一个可行解)。
由于第二种算法和已介绍的最大流算法接近,且算法中寻找最小费用增流链,可以转化为一个寻求源点至汇点的最短路径问题,所以这里介绍这一算法。
在这一算法中,为了寻求最小费用的增流链,对每一当前流,需建立伴随这一网络流的增流网络。例如图 1 网络G 是具有最小 费用的流,边旁参数为c(e),f(e),w(e),而图 2 即为该网络流 的增流网络G′。增流网络的顶点和原网络相同。按以下原则建 立增流网络的边:若G中边(u,v)流量未饱,即f(u,v) < e(u,v),则G ' 中建边(u,v),赋权w ' (u,v)=w(u,v);若G中边(u,v)已有流量,即f(u,v)〉0,则G′中建边(v,u),赋权w′(v,u) =-w(u,v)。建立增流网络后,即可在此网络上求源点至汇点的最短路径,以此决定增流路径,然后在原网络上循此路径增流。这里,运用的仍然是最大流算法的增流原理,唯必须选定最小费用的增流链增流。
计算中有一个问题需要解决。这就是增流网络G ′中有负权边,因而不能直接应用标号法来寻找x至y的最短路径,采用其它计算有负权边的网络最短路径的方法来寻找x至y的最短路径,将 大大降低计算效率。为了仍然采用标号法计算最短路径,在每次建立增流网络求得最短路径后,可将网络G的权w(e)做一次修正,使再建的增流网络不会出现负权边,并保证最短路径不至于因此而改变。下面介绍这种修改方法。当流值为零,第一次建增流网络求最短路径时,因无负权边,当然可以采用标号法进行计算。为了使以后建立增流网络时不出现负权边,采取的办法是将 G中有流边(f(e)>0)的权w(e)修正为0。为此, 每次在增流网络上求得最短路径后,以下式计算G中新的边权w " (u,v):
w " (u,v)=L(u)-L(v) w(u,v) (*)
式中 L(u),L(v) -- 计算G′的x至y最短路径时u和v的标号值。第一次求最短径时如果(u,v)是增流路径上的边, 则据最短 路径算法一定有 L(v)=L(u) w ' (u,v)=L(u) w(u,v), 代入(*)式必有
w″(u,v)=0。
如果(u,v)不是增流路径上的边,则一定有:
L(v)≤L(u) w(u,v), 代入(*)式则有 w(u,v)≥0。
可见第一次修正w(e)后,对任一边,皆有w(e)≥0, 且有流 的边(增流链上的边),一定有w(e)=0。以后每次迭代计算,若 f(u,v)>0,增流网络需建立(v,u)边,边权数w ' (v,u)=-w(u,v) =0,即不会再出现负权边。 此外,每次迭代计算用(*)式修正一切w(e), 不难证明对每一条x至y的路径而言,其路径长度都同样增加L(x)-L(y)。因此,x至y的最短路径不会因对w(e)的修正而发生变化。
【计算步骤】
⒈ 对网络G=[V,E,C,W],给出流值为零的初始流。
⒉ 作伴随这个流的增流网络G′=[V′,E′,W′]。G′的顶点同G:V′=V。若G中f(u,v)0,则G′中建边(v,u),w′(v,u)=-w(u,v)。
⒊ 若G′不存在x至y的路径,则G的流即为最小费用最大流, 停止计算;否则用标号法找出x至y的最短路径P。
⒋ 根据P,在G上增流:对P的每条边(u,v),若G存在(u,v),则(u,v)增流;若G存在(v,u),则(v,u)减流。增(减)流后,应保证对任一边有c(e)≥ f(e)≥0。
⒌ 根据计算最短路径时的各顶点的标号值L(v),按下式修 改G一切边的权数w(e):
L(u)-L(v) w(e)→w(e)。
⒍ 将新流视为初始流,转2。
前向弧和后向弧
在网络D(V,A) 中,如果对连接发点vs和收点vt 的一条链P,方向规定为从vs 到vt,则当链P 中弧(vi,vj)
的方向与规定的方向一致时,称弧(vi,vj) 为前向弧,否则称为后向弧。不在这条链上的弧,不定义前向弧和后向弧。
可扩充链
设{fij}为一可行流(假设为非负值),如果存在从发点vs 到收点vt 的链P,在链P 上,下列两条同时满足,则称P 为可扩充链:
①对于P 上的前向弧(vi,vj) 有fij
②对于P 上的后向弧(vi,vj) 有fij>0。
可扩充链P的费用
设对于可行流f 存在可扩充链P,当以ε=1 调整f 而得到可行流f' 时,两流的费用之差成为可扩充链p 的费用。其中P 和P- 分别表示p 上的前向弧和后向弧。
求助官方客服吧程序的问题,官方客服是最好的专家的
试一下Ctrl+Tab组合键等一会
根据《室外排水设计规范》平流沉砂池的设计,应符合下列要求:1 最大流速应为0.3m/s,最小流速应为0.15m/s;2 最高时流量的停留时间不应小于30s;3 有效水深不应大于1.2m...

 梁、柱最大最小配筋率
梁、柱最大最小配筋率
梁、柱最大最小配筋率
梁、柱最大最小配筋率
最小费用最大流问题是经济学和管理学中的一类典型问题。在一个网络中每段路径都有“容量”和“费用”两个限制的条件下,此类问题的研究试图寻找出:流量从A到B,如何选择路径、分配经过路径的流量,可以达到所用的费用最小的要求。
在实际中:n辆卡车要运送物品,从A地到B地。由于每条路段都有不同的路费要缴纳,每条路能容纳的车的数量有限制,如何分配卡车的出发路径可以达到费用最低,物品又能全部送到。
在图论中,网络流(英语:Network flow)是指在一个每条边都有容量(capacity)的有向图分配流,使一条边的流量不会超过它的容量。通常在运筹学中,有向图称为网络。顶点称为节点(node)而边称为弧(arc)。一道流必须匹配一个结点的进出的流量相同的限制,除非这是一个源点(source)──有较多向外的流,或是一个汇点(sink)──有较多向内的流。一个网络可以用来模拟道路系统的交通量、管中的液体、电路中的电流或类似一些东西在一个结点的网络中游动的任何事物。
由割集的定义不难看出,无论拿掉那个割集,发点vs到收点vt便不再相通,所以任何一个可行流都会经过割集,且不会超过任一割集的容量。最小割如同瓶颈一般,即使是最大流也无法超过最小割,网络的最大流与最小割容量满足下面的定理(证明略)。
设f为网络G=(V,E,C)的任一可行流,流量为v(f),
由定理一可知,最大流的流量v(f)和某一割集K的容量相等,而且最大流的流量本身也不带任一割集的容量,因此割集一定是最小的割集。
任一网络G中,从vs到vt的最大流的流量等于分离vs、vt的最小割的容量(最小的割集的容量)。
一条从起点vs到终点vt的链μ,规定从vs到vt的方向为链μ的方向,链上与μ方向一致的边叫前向弧(边),记作μ-;与μ方向相反的边称为后向弧(边),记作μ 。
f是一个可行流,fij表示由i点指向j点的流量,如果满足前向弧的流量非负且小于容量,或后向弧的流量大于0且不超过容量:
则称μ为从vs到vt的关于f的可增广链。
可增广链的实际意义是:沿着这条从vs到vt输送的流,仍有潜力可挖,只要前向弧的流量增加或后向弧的流量减少,就可以将截集的流量提高。调整后的流,在各点仍满足平衡条件及容量限制条件,仍为可行流。
从另一个角度来说,可以提高流量的可行流也不是最大流,因此可行流f是最大流的充要条件是不存在从vs到vt的可增广链。