选择特殊符号

Ф δ ° × # Ⅱ Ⅲ ½ ¼

选择搜索类型

市场价信息价参考价询价供应商云知资讯文库百科

热门搜索

造价通

请输入搜索

首页 > 百科 > 建设工程百科

直线相关和曲线相关

直线相关和曲线相关是指两个变量之间的相关关系能近似地用一条直线表示。如原材料消耗量与生产费用额之间的关系等。

直线相关和曲线相关简介

直线相关和曲线相关是指两个变量之间的相关关系能近似地用一条直线表示。如原材料消耗量与生产费用额之间的关系等。 曲线相关是指两个相关变量的相关关系能近似地用一条曲线表示。如产品产量与单位产品成本之间的关系。曲线相关可按曲线形状分为不同种类，如抛物线、双曲线等。 2100433B

直线相关和曲线相关造价信息

市场价
信息价
询价

线缆及相关附件

规格型号：
VGA/DVI
价格行情：
材料单位：
套
材料品牌：
彩讯
材料税率：
13%
供应商：
深圳高创科技有限公司
报价时间：
2022-12-07

查看价格

曲线拉板

规格型号：
品种:曲线拉板;说明:铁附件;类型:曲拉板;外形尺寸(mm):40×4×250;表面处理:热镀;
价格行情：
材料单位：
副
材料品牌：
浩川
材料税率：
13%
供应商：
银川浩川电力设备有限公司
报价时间：
2022-12-07

查看价格

C曲线小型断路器

规格型号：
PSC6-63 3A/1P 10KA 5-10In
价格行情：
材料单位：
个
材料品牌：
鹏升
材料税率：
13%
供应商：
广州市鹏升电器设备有限公司
报价时间：
2022-12-07

查看价格

C曲线小型断路器

规格型号：
PSC6-63 25A/1P 10KA 5-10In
价格行情：
材料单位：
个
材料品牌：
鹏升
材料税率：
13%
供应商：
广州市鹏升电器设备有限公司
报价时间：
2022-12-07

查看价格

C曲线小型断路器

规格型号：
PSC6-63 50A/1P 10KA 5-10In
价格行情：
材料单位：
个
材料品牌：
鹏升
材料税率：
13%
供应商：
广州市鹏升电器设备有限公司
报价时间：
2022-12-07

查看价格

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2020年6月信息价
所属行业：
建筑工程
备注说明：

查看价格

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2020年5月信息价
所属行业：
建筑工程
备注说明：

查看价格

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2019年9月信息价
所属行业：
建筑工程
备注说明：

查看价格

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2019年4月信息价
所属行业：
建筑工程
备注说明：

查看价格

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2019年3月信息价
所属行业：
建筑工程
备注说明：

查看价格

网线及相关设备

规格型号：
气动物流
需求量：
5350m
报价数：
1
材料品牌：
上海银翼
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2021-11-11

查看价格

全省柔性引才相关信息展示

规格型号：
全省柔性引才相关信息展示
需求量：
1套
报价数：
1
材料品牌：
材料档次：
高档
费用说明：
不含税费 | 不含运费
询价时间：
2022-01-07

查看价格

技能人才培养相关展示

规格型号：
技能人才培养相关展示
需求量：
1套
报价数：
1
材料品牌：
材料档次：
高档
费用说明：
不含税费 | 不含运费
询价时间：
2022-01-07

查看价格

技能大赛相关人才信息展示

规格型号：
技能大赛相关人才信息展示
需求量：
1套
报价数：
1
材料品牌：
材料档次：
高档
费用说明：
不含税费 | 不含运费
询价时间：
2022-01-07

查看价格

曲线攀爬

规格型号：
详见图纸
需求量：
1个
报价数：
3
材料品牌：
-
材料档次：
中高档
费用说明：
不含税费 | 含运费
询价时间：
2022-08-19

查看价格

直线相关和曲线相关常见问题

缓和曲线怎么算？

5800手机应该不行，电脑上可以CAD 使用SPLINE命令。
各位，请问怎么判别缓和曲线类型，什么是回旋曲线，复曲线还有S型曲线，曲线完整与不完整等？

可做为缓和曲线的曲线有多种，如：双纽曲线、高次抛物线，正选曲弦、样条曲线、回旋曲线等，其中考虑到回旋曲线与车辆由直线进入圆曲线行驶的轨迹比较吻合，更重要的是回旋线计算起来比较简单，因此道路《规范》...
直线、曲线转角表上，怎么算缓和曲线段的方位角，两个半径怎么算，不一样，用哪个？

以曲中点断开，曲中点以前得用一个半径，以后的用一个半径。

直线相关和曲线相关文献

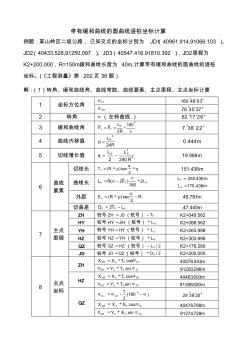带有缓和曲线的圆曲线逐桩坐标计算例题

带有缓和曲线的圆曲线逐桩坐标计算例题

带有缓和曲线的圆曲线逐桩坐标计算例题

格式：pdf

大小：542KB

页数： 5页

带有缓和曲线的圆曲线逐桩坐标计算例题：某山岭区二级公路，已知交点的坐标分别为 JD1（40961.914,91066.103 ）、 JD2（40433.528,91250.097 ）、JD3（40547.416,91810.392 ），JD2里程为 K2+200.000，R=150m,缓和曲线长度为 40m,计算带有缓和曲线的圆曲线的逐桩坐标。（《工程测量》第 202页 36题）解：（1）转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计算 1 坐标方位角 12 3084160 23 730378 2 转角（左转曲线） 627182 3 缓和曲线角 180 2R LS ho 22837 4 曲线内移值 R L p S 24 2 m444.0 5 切线增长值 2 3 2402 R LLq SS m988.19 6 曲线要素切线长 qpRTh 2 tan)( m438.

在线阅读立即下载

道路施工中有缓和曲线的圆曲线放样

道路施工中有缓和曲线的圆曲线放样

道路施工中有缓和曲线的圆曲线放样

格式：pdf

大小：542KB

页数： 3页

在线阅读立即下载

相关曲线图简介

相关曲线图，亦称依从关系曲线图。是指用以表明社会现象之间相互关系的曲线图。反映某一现象的变化受另一现象变化的影响程度。图的纵横两轴（x轴和y轴）分别表示两个相互关联的不同现象。 通常把起影响作用的现象表示在横轴上，把被影响的现象表示在纵轴上，如果纵轴的指标数值随着横轴指标数值的增大而减小，则表示两个现象之间存在反方向的依存关系即负相关。用曲线表示数字资料的统计图。在直角坐标中利用一根或几根曲线的升降起伏来表示社会现象的数量变动情况及其发展趋势的图形。2100433B

样条曲线曲线相关性质

样条曲线曲线段 样条曲线是由一组逼近控制多边形的光滑参数曲线段构成，这些曲线段就是样条曲线段。 特征多边形/控制多边形的顶点/控制点 构成特征多边形的各段折线的端点，就是特征多边形的顶点，也叫做控制多边形的控制点。只有在特殊情况下，样条曲线才能通过控制点。 样条曲线曲线次数 样条曲线的次数，是由样条曲线数学定义中所取的基函数所决定的。直观的说，所构成样条曲线的一段光滑参数曲线段，由控制多边形的相邻连续的几段折线段决定，就是几次样条，最常用的就是二次和三次样条。二次样条的某一曲线段只与相应的两段折线段，三个控制多边形顶点有关，改变其中一个顶点，将影响三段样条曲线段。同样的，对三次样条，某一曲线段由相应的三段折线段，四个控制点决定。 样条曲线曲线阶数 阶数与次数有关，样条曲线的阶是其次数加一。阶数越高，控制点越多。二次样条的阶数是三，样条曲线段由三个控制点决定；三次样条的阶数是四，样条曲线段与四个控制点决定。 样条曲线曲线权值 权值可控制样条曲线段在控制多边形范围内做局部调整，反映了曲线靠近控制多边形的程度，权值越大，曲线段越靠近控制多边形。反之，则远离。当权值为1时，NURBS曲线退化为非有理B样条曲线，可见非有理B样条曲线是NURBS的一个子集。 样条曲线曲线允差 允差是指样条曲线通过型值点的精确程度，允差越小，样条曲线与型值点越接近，允差为零，样条曲线将通过型值点。

曲线积分相关概念

曲线积分积分联系 对弧长的曲线积分和对坐标轴的曲线积分是可以互相转化的，利用弧微分公式 ，或者 ；这样对弧长的曲线积分都可以转换成对坐标轴的曲线积分了。 在曲线积分中，被积的函数可以是标量函数或向量函数。积分的值是路径各点上的函数值乘上相应的权重（一般是弧长，在积分函数是向量函数时，一般是函数值与曲线微元向量的标量积）后的黎曼和。带有权重是曲线积分与一般区间上的积分的主要不同点。物理学中的许多简单的公式（比如说）在推广之后都是以曲线积分的形式出现（ ）。曲线积分在物理学中是很重要的工具，例如计算电场或重力场中的做功，或量子力学中计算粒子出现的概率。 曲线积分量子力学 量子力学中的“曲线积分形式”和曲线积分并不相同，因为曲线积分形式中所用的积分是函数空间上的泛函积分，即关于空间中每个路径的概率函数进行积分。然而，曲线积分在量子力学中仍有重要作用，比如说复围道积分常常用来计算量子散射理论中的概率振幅。 曲线积分复分关系 如果将复数看作二维的向量，那么二维向量场的曲线积分就是相应复函数的共轭函数在同样路径上的积分值的实部。根据柯西-黎曼方程，一个全纯函数的共轭函数所对应的向量场的旋度是0。 曲线积分应用简介 在各种保守力的场都是路径无关的，一个常见的例子就是重力场或电场。在计算这种场的做功时，可以选择适当的路径进行积分，使得计算变得简单。如： 。2100433B

相关推荐

相关百科
相关知识
相关专栏

免费服务热线: 400-888-9639