1.全等的任意三角形能镶嵌平面
把一些纸整齐地叠放好，用剪刀一次即可剪出多个全等的三角形.用这些全等的三角形可镶嵌平面.这是因为三角形的内角和是180°，用6个全等的三角形即可镶嵌出一个平面.如图1.
用全等的三角形镶嵌平面，镶嵌的方法不止一种，如图2.
2.全等的任意四边形能镶嵌平面。
仿上面的方法可剪出多个全等的四边形，用它们可镶嵌平面.这是因为四边形的内角和是360°，用4个全等的四边形即可镶嵌出一个平面.如图3.其实四边形的平面镶嵌可看成是用两类全等的三角形进行镶嵌.如图4.
3.全等的特殊五边形可镶嵌平面
圣地亚歌一位家庭妇女，五个孩子的母亲玛乔里·赖斯，对平面镶嵌有很深的研究，尤其对五边形的镶嵌提出了很多前所未有的结论.1968年克什纳断言只有8类五边形能镶嵌平面，可是玛乔里·赖斯后来又找到了5类五边形能镶嵌平面，在图5的五边形ABCDE中，∠B=∠E=90°，2∠A+∠D=2∠C+∠D=360°，a=e，a+e=d.图6是她于1977年12月找到的一种用此五边形镶嵌的方法.用五边形镶嵌平面，是否只有13类，还有待研究.
4.全等的特殊六边形可镶嵌平面
1918年，莱因哈特证明了只有3类六边形能镶嵌平面.图7是其中之一.在图7的六边形ABCDEF中，∠A+∠B+∠C=360°，a=d.
5.七边形或多于七边的凸多边形，不能镶嵌平面.
只有正三角形、正方形和正六边形可镶嵌平面，用其它正多边形不能镶嵌平面.
所有的方法:
用1种:(3，3，3，3，3，3)(4，4，4，4)(6，6，6);
用2种:(4，8，8)(3，12，12)(3，3，6，6)(3，3，3，3，6)(3，3，3，4，4)(*5，10，10)
用3种:(3，4，4，6)(4，6，12)(3，3，4，12)(3，10，15)(3，9，18)(3，8，24)(3，7，42)(*4，5，20)
其中的数字分别代表正多边形的边数。共有17种。
是枚举出来的。
证明不能用3种以上的多边形镶嵌:
因为若用4种，则内角和最小为60+90+108+120=378>360，(三角形、正方形、正五边形、正六边形)。
另外其中带星号的的两个(5,10,10)(3,7,42)是只能在一个点镶嵌，而不能在整个平面镶嵌。不带这两个，则是有15种方法。
例如:用正三角形和正六形的组合进行镶嵌.设在一个顶点周围有m个正三角形的角，有n个正六边形的角.由于正三角形的每个角是60°，正六边形的每个角是120°.所以有
m·60°+n·120°=360°，即m+2n=6.
这个方程的正整数解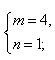
或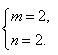
可见用正三角形和正六边形镶嵌，有两种类型，一种是在一个顶点的周围有4个正三角形和1个正六边形，另一种是在一个顶点的周围有2个正三角形和2个正六边形.如图8、图9.
