阿基米德螺线 ，亦称"等速螺线"。当一点P沿动射线OP一等速率运动的同时，这射线有以等角速度绕点O旋转，点P的轨迹称为"阿基米德螺线"。
它的极坐标方程为:r = aθ
这种螺线的每条臂的距离永远相等于 2πa。
笛卡尔坐标
方程式为:
r=10*(1+t)
x=r*cos(t * 360)
y=r*sin(t * 360)
z=0
一动点沿一直线作等速移动的同时，该直线又绕线上一点O作等角速度旋转时，动点所走的轨迹就是阿基米德涡线。直线旋转一周时，动点在直线上移动的距离称为导程用字母S表示。
阿基米德涡线在凸轮设计、车床卡盘设计、涡旋弹簧、螺纹、蜗杆设计中应用较多。阿基米德涡线画法如图:
(1)先以导程S为半径画圆，再将圆周及半径分成相同的n等分，图中n=8;
(2)以O为圆心，作各同心圆弧于相应数字的半径相交，得交点Ⅰ、Ⅱ、Ⅲ、…Ⅷ各点，即为阿基米德涡线上的点;
(3)依次光滑连接各点，即得阿基米德涡线。
与希皮亚斯割圆曲线相类似，阿基米德螺线不但可以用来三等分角，也可以用来化圆为方。不过，后者也是阿基米德自己完成的。如图一，螺线P=aθ的极点为O，第一圈终于点A。以O为圆心，a为半径作圆，则圆周长等于=OA。这样，阿基米德轻易解决化圆为方问题。
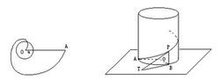稍迟于阿基米德的阿波罗尼斯用圆柱螺线解决了化圆为方问题，如图4-2-27所示。设圆O是一直圆柱之底面，A是螺旋线之起始点。螺旋线在其上任一点P处的切线交底所在平面于T。则PT在底平面上的投影BT与AB相等。因此，当P点恰好为A点所在母线上离A最近的点时，TB与圆周长相等。 从而化圆为方问题得以解决。
在阿波罗尼斯之后，机械师卡普斯(Carpus)也解过化圆为方问题。他所用的"双重运动曲线"今已失传，据数学史家唐内里(P. Tannery, 1843~1904)推测，它是摆线，亦即卡普斯是通过将圆沿直线滚动一周获得圆周长的(图二)。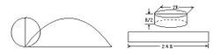
文艺复兴时期，意大利著名艺术大师达·芬奇(1452~1519)为化圆为方问题所吸引，并获巧妙方法。如图4-2-29，设圆半径为R，以圆为底作高为R/2的圆柱，然后将圆柱在平面上滚动一周，得矩形。 将矩形化方，即完成化圆为方。
以上我们看到，希腊人很早就意识到(但未能证明)三大难题不能以尺规在有限步骤内完成。但它们看似如此简单，以至希腊人未能抵制诱惑;他们不断寻求尺规以外的方法，结果导致圆锥曲线、割圆曲线、蚌线、蔓叶线和螺线等高次曲线和超越曲线的相继发现。三大难题使一代又一代希腊数学家显示了非凡的聪明才智，并深刻影响了希腊几何的整个发展过程。
三大难题的魅力并未随希腊文明的沦亡而消失。事实上，从希腊以后特别是欧洲文艺复兴时期以来直到本世纪，对于它们的研究从未停止过。
1837年，年轻的法国数学家万采尔(P. L. Wantzel，1814~1848)证明了三等分角和倍立方尺规作图之不可能性。1882年，德国数学家林德曼(C. Lindemann, 1852~1938)证明了π的超越性，从而证明了化圆为方的尺规作图之不可能性。以后数学家们又还建立了两条一般定理:
定理1 任何可用尺规由已知单位长度作出的量必为代数数;
定理2 若一有理系数三次方程没有有理根，则它的根不可能用尺规由一给定单位长度作出。
