逆反射的实现,是一种人工新技术的实现过程,因此,如何测试和科学准确地定义这种技术的实现效果,对交通安全技术应用,具备非常重要的意义。本节主要介绍我国有关逆反射测试的技术基础。
规范逆反射术语定义,是认识和发展逆反射技术的前提条件,也是逆反射测试的基础工作。逆反射概念及其相关术语定义,在我国交通行业标准JT/T 688-2007《逆反射术语》中有详细描述。主要术语定义如下:
1逆反射:反射光从接近入射光的反方向返回的一种反射。当入射光方向在较大范围内变化时,仍能保持这种性质。现实中可通过两种结构方式实现该种反射:玻璃珠结构和棱镜结构。
2逆反射材料:具备逆反射特性的材料统称,在暴露的表面或接近表面有一层薄的、连续的微小逆反射元素的反射层。例如反光膜、反光片、道路交通标线等。
3逆反射体:具有逆反射性能的一种反光面或器件。具备逆反射特性的物体统称,在学术研究中使用较多。
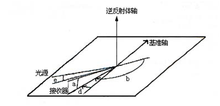
4逆反射体轴:从逆反射体中心发出的一条特定的射线。逆反射体轴通常选择照明方向的中心线。当逆反射体为轴对称时,逆反射体轴通常与逆反射体的对称轴一致。对于路面标线,逆反射体轴垂直于路面。
5基准轴:从逆反射体中心发出,垂直于逆反射体轴的一条射线。基准轴与逆反射体中心、逆反射体轴给出逆反射体的位置。
6照明轴:从逆反射体中心发出的通过光源的射线。
7观测轴:从逆反射体中心通过观测点的射线。
8第一轴:通过逆反射体中心且垂直于观测半平面的轴。
9第二轴:该轴通过逆反射体中心,在照明轴和观测轴平面内,垂直于逆反射体轴。
10入射角β:照明轴和逆反射体轴之间的夹角。入射角通常不大于90º,但考虑完整性将其规定为0º≤β≤180º。在角度计系统中β被分解为β1和β2两个分量。国内外道路交通安全测试技术相关标准中,入射角一般取4º、5º、10º、15º、20º、30、40º。
11入射角分量β1:照明轴与包含逆反射体轴和第一轴的平面之间的夹角。-180º<β1≤180º。
12入射角分量β2:观测半平面与逆反射体轴之间的夹角。-90º≤β2≤90º。对于一些测试,扩展到-180º<β2≤180º,此时-90º<β1≤90º。
13观测角α:照明轴与观测轴之间的夹角。观测角不为负值,一般小于10º,通常小于2º。全部范围定义为0º≤α<180º。国内外道路交通安全测试技术相关标准中,观测角一般取0.1º、0.2º、0.33º、0.5º、1º。
14旋转角ε:从逆反射体轴上的观察点逆时针测量,在垂直于逆反射体轴的平面上,从观测半平面到基准轴的夹角。-180º<ε≤180º。入射角和视角小于90º时定义是适当的。更多情况下,旋转角是从逆反射体轴的观察点逆时针测量,第二轴到基准轴的相反部分。
15视角ν:逆反射体轴和观测轴之间的夹角。角度计系统中cosν=cos(β1-α)cosβ2。当视角接近90º时,对于路面标线,一般情况下使用视角的余角即余视角a。
16方位角ωs:位于垂直于逆反射体轴的平面内,从光源观察点逆时针测量,从入射半平面到基准轴之间的夹角。ωs值在-180º与180º之间。试样围绕逆反射体轴转动时,当光源和接收器在空间相对固定,方位角(ωs)和旋转角(ε)的变化是相等的。
17道路标线方位角b:从逆反射体轴的观察点顺时针测量,入射半平面与从逆反射体轴发出包含观测轴的半平面之间的夹角。b 值在-180º与180º之间。
18道路标线方位角补角d:从逆反射体轴的观察点顺时针测量,垂直于逆反射体轴的平面上基准轴与从逆反体轴发出包含观测轴的半平面之间的夹角。d 值在-180º与180º之间。
19显示角γ:从光源观察点逆时针测量,从入射半平面到观测半平面的二面角。γ值在-180º与180º之间。
20 rho角ρ :从光源观察点逆时针测量,观测半平面与从照明轴发出包含基准轴的半平面之间的二面角。
在规范逆反射术语定义的基础上研究逆反射测试技术,对逆反射性能进行定量分析和质量监控,是逆反射技术的重要内容之一。逆反射测试系统主要包括如下内容:
系统综述
描述光源、接收器和样品之间的几何关系时,角度的组合非常重要。在任何系统中,通过四个角度中的任何一个都可以计算得出其它角度。逆反射描述主要有下面四个系统:
1. {α、β1、β2、ε} CIE角度计系统
2. {α、β、γ、ωs} 固有系统
3. {α、β、ε、ωs} 应用系统
4. {a、b、e、d} 道路标线系统
其中α、β、ε、ωs、γ之间的关系见图10。
前三个系统是球形的,样品中的任何地方都可以被照明和接收。第四个系统是半球形的。
第一个系统通常用于特殊的实验室测试;第二系统和第三个系统通常用于对大多数逆反射体性能的研究;第四个系统通常用于对逆反射体入射角余角性能的研究。
CIE角度计系统
CIE角度计系统是基于逆反射体的角度测量方法,相对容易建立,而且容易使实验室间达成一致,因而被ASTM标准所推荐。
图11中标明了CIE角度计系统的{α、β1、β2、ε}。这四个CIE角度在逆反射测量仪中随三维变化而被精确测量。第一轴垂直于包含观测轴和照明轴的平面。第二轴垂直于逆反射体轴,位于包含观测轴和照明轴的平面内。所有轴、角度和方向都为正值。

样品角度计的三维运动使角度β1、β2和ε发生变化,角度的大小根据样品的测试要求而设置,如图12所示。样品必须是固定的,逆反射体轴垂直于样品表面。

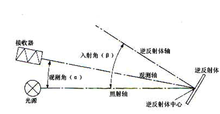
无下标的入射角β容易引起歧义,在有些地方被认为是±β1,有些地方则被认为是±β2,造成不同国家实验室目前存在两种不同的几何测试方法:"水平测试法"和"垂直测试法"。图13表示的是基于"水平测试法"和"垂直测试法"的共平面几何测试方法。这两种不同的测试方法对于玻璃珠型逆反射体的测试结果影响较小,对棱镜型逆反射体的测试则存在严重影响。所以建议在逆反射描述中,β1和β2都必须指定,即使其中一个是零也应予以明确。图中说明了入射半平面和观测半平面在同一平面内的测试情况,入射角β和观测角 都为正值。该图没有显示转动角ε。注2:在该图中β是正值,用终止于逆反射体轴的单向箭号表示,相当于CIE系统中:β=β1,β2=0。
固有系统
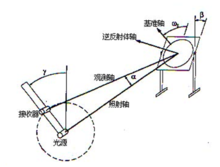
固有系统{α、β、γ、ωs }可由设定了α和γ的两轴观测者角度计和设置了β和ωs的两轴样品角度计的逆反射测量仪来表示。逆反射体测量仪可以使用一个常用的设定角度α的一轴观测者角度计,也可以使用一个设定角度β、γ和ωs的结构合理的三轴样品角度计。固有系统的角度{α、β、γ、ωs }包含在图14中。
棱镜型逆反射体的表示方法完全依赖该系统的四个角,玻璃珠型的逆反射体则依赖于角α、β和γ。逆反射体轴是样品角度计平面的法线,角ωs和γ是正值,接收器的转动轨迹围绕着照明轴,转动角用γ表示,为了避免冗余,β的移动在方向上是受限制的。注2:固有系统与CIE(角度计)系统有关,其中的入射角β和显示角γ,几何上等同于一对入射角分量β1和β2。
应用系统
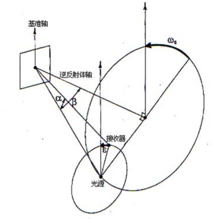
应用系统{α、β、ε、ωs }(图2-15)从观测几何条件(α、ε)中分离出了照明几何条件(β、ωs)。转动角ε和ωs都是根据样品基准轴来定义的。图16包含了应用系统中的角度{α、β、ε、ωs }。
该系统在研究各种道路应用中遇到的几何问题时是很有用的。棱镜型逆反射体的性能很明显依赖于该系统的这四个角度。
没有一个简单的角度计可以表示这个角度系统。为了使这一系统得到应用,需要将角度转换到一个更好的计算机化的逆反射测量系统中。角ωs和ε位于垂直于逆反射体轴的平面内,用正值表示。注2:在这一系统中,当对对称转动的逆反射体进行测量时,需要对角ε和ωs同时进行定义,因为这些逆反射体的逆反射性能主要体现在不同的ωs-ε值上。注3:相似系统{α、β、ρ、ωs }对研究光通量和衍射上是很有用的。
道路标线系统
道路标线系统{a、b、e、d}(图16)特指接近于平面的道路标线。该系统通常使用RM中的{a、e}两个角度来限制。道路标线通常是在b=180,d=0的情况下测量的,严格地说,这四个角度都要求进行指定,特别是对于非对称转动的道路标线系统。(注:该RM系统和欧洲道路照明系统(RL)是一致的,只是用不同的角度符号来表示和定义。{a、b、e、d}是RM中的定义,{α、β、ε、δ}则是RL中的定义。RL中的角度ε在RL中被定义为90-γ。)角d和角b用正值表示,一般情况下d=0º,同时b=180º,并且a>e。在测试中,接收器位于光源的上方。