将均匀长线分成许多长度元dχ，其中之一见图1a。对该长度元忽略参数的分布性，可得出其集总参数电路模型(图1b)。将每个长度元都这样处理后，得出的由许多集总参数电路作为环节级联而成的链形电路就是整个均匀长线的电路模型。若设图1a所示长度元的A点和B点距长线的始端的距离分别为χ和χ+dχ;在某一瞬间A点的电压为V，电流为I;在B点的电压为V+dV,电流为I+dI， 则对此长度元的集总参数电路模型(图1b)可用KVL和KCL导出偏微分方程组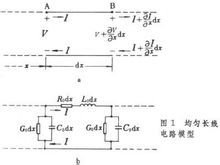通常称为亥维赛电报方程。在正弦稳态下，使用电压和电流的相量可将上述方程组化为

式中Z0称为线阻抗，Y0称为线导纳。 联立式(5)和式(6)求解，可得电压和电流的正弦稳态解

式中A1和A2是需要根据边界条件定出的两个常数，通常都是复数,可分别记为A1=a1e拸$和A2=a2e拹$

行波、入射波和反射波 长线的一个明显的特征是其电压和电流正弦稳态解中的两个分量的波形皆随时间的变化而沿线移动。这种沿线向一个方向移动的波称为行波。将式(7)和式(8)改写成瞬时值形式

便容易证实这一点。电压表达式右端第一项代表的电压分量VI(χ ,t) 是以速度(称为相速或波速)

沿线向χ 增加方向传播的行波，而且随着波的前进，振幅按因子 e-βχ决定的指数律衰减。这个从始端向终端传播的行波称为电压入射波。图2a表示出 t=t0和t=t0+Δt时的VI(χ ,t)曲线。同样，电流分量IφI(χ ,t)也是一个行波，称为电流入射波。电压(电流)的另一个分量VR(χ,t)·【IR(χ,t)】也是一个行波，波速也是vp。但由于相位中与χ 有关的项是αχ,而不是-αχ,所以这个波的传播方向与VφI(χ ,t)【IφI(χ ,t)】的传播方向相反。另外,由于因子eβχ随χ的减少而减少，其振幅也随着波的前进而逐渐衰减。这个从终端向始端传播的行波称为电压(电流)反射波。图2b表示的是电压反射波VR(χ ,t)的波过程。 式(9)和式(10)的 β和α分别称为衰减系数和相位系数。前者决定波振幅衰减的快慢，后者决定波相位变化的快慢。