到另一对角线的两个端点的距离相等，则称这点为这个四边形的准等距点.如图l.

(1)如图2，画出菱形ABCD的一个准等距点.

(2)如图3，作出四边形ABCD的一个准等距点(尺规作图，保留作图痕迹，不要求写作法).

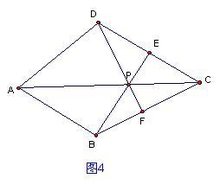
(3)如图4，在四边形ABCD中，P是AC上的点，PA≠PC，延长BP交CD于点E，延长DP交BC于点F，且∠CDF=∠CBE，CE=CF.求证:点P是四边形AB CD的准等距点.

(4)试研究四边形的准等距点个数的情况(说出相应四边形的特征及准等距点的个数，不必证明).

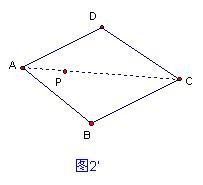
解:(1)如图2'中，点P即为所画点.(因为菱形的对角线互相垂直平分，所以在直线AC上除线段AC中点外的任意一点都符合条件)

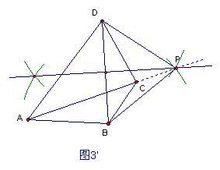(2)如图3'中，点P即为所作点.(线段BD的垂直平分线与直线AC的交点)

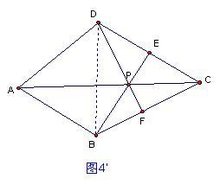(3) 如图4'中，连结DB，

在△DCF与△BCE中，

∠DCF=∠BCE，

∠CDF=∠CBE，

∠ CF=CE.

∴△DCF≌△BCE(AAS)，

∴CD=CB，

∴∠CDB=∠CBD.

∴∠PDB=∠PBD，

∴PD=PB，

∵PA≠PC

∴点P是四边形ABCD的准等距点.

(4)①当四边形的对角线互相垂直且任何一条对角线不平分另一对角线或者对角线互相平分且不垂直时，准等距点的个数为0个;