
(经典的卡塞格林系统):
"传统的"卡塞格林望远镜有抛物面镜的主镜,和双曲面的次镜将光线反射并穿过主 镜中心的孔洞,折叠光学的设计使镜筒的长度紧缩。在小望远镜和照相机的镜头,次镜通常安装在封闭望远镜镜筒的透明光学玻璃板上的光学平台。这样的装置可以消除蜘蛛型支撑架造成的"星状"散射效应。封闭镜筒虽然会造成集光量的损失,但镜筒可以保持干净,主镜也能得到保护。
镜中心的孔洞,折叠光学的设计使镜筒的长度紧缩。在小望远镜和照相机的镜头,次镜通常安装在封闭望远镜镜筒的透明光学玻璃板上的光学平台。这样的装置可以消除蜘蛛型支撑架造成的"星状"散射效应。封闭镜筒虽然会造成集光量的损失,但镜筒可以保持干净,主镜也能得到保护。
它利用双曲面和抛物面反射的一些特性,凹面的抛物面反射镜可以将平行于光轴入射的所有光线汇聚在单一的点上-焦点;凸面的双曲面反射镜有两个焦点,会将所有通过其中一个焦点的光线反射至另一个焦点上。这一类型望远镜的镜片在设计上会安放在共享一个焦点的位置上,以便光线能在双曲面镜的另一个焦点上成像以便观测,通常外部的目镜也会在这个点上。抛物面的主镜将进入望远镜的平行光线反射并汇聚在焦点上,这个点也是双曲线面镜的一个焦点。然后双曲面镜将这些光线反射至另一个焦点,就可以在那儿观察影像.
(R-C系统,里奇克列基昂):
平行于光轴的光﹐满足等光程和正弦条件的卡塞格林望远镜。它是由克列基昂(H.Chretien)提出﹑里奇(G.W.Ritch)制成的﹐按他们两人姓氏的第一个字母得名为R-C望远镜。它的焦点称为R-C 焦点。这种望远镜的主﹑副镜形状很接近旋转双曲面﹐在实用上可把这种系统近似地视为消除三级球差和彗差的﹑由旋转双曲面组成的系统。由于消除了彗差﹐可用视场比其他形式的卡塞格林望远镜更大一些﹐并且像斑呈对称的椭圆形。如果采用弯曲底片﹐视场会更明显地增大﹐像斑则呈圆形。一个主镜相对口径为1/3﹑系统相对口径为1/8﹑且像成在主镜后面不远处的这种望远镜﹐其主镜偏心率接近于1.06的双曲面﹐副镜偏心率接近于2.56的双曲面。在理想像平面(近轴光的像平面)上﹐如要求像斑的弥散不超过1﹐可用视场直径约为19'﹔如用弯曲底片﹐仍要求像斑的弥散不超过1﹐则视场直径可达37'。如要获得更大的视场﹐则需加入像场改正透镜。加入像场改正的R-C望远镜比主镜为抛物面的卡塞格林望远镜的效果也更好。但在R-C望远镜中使用主焦点时﹐所成的像是有球差的。因此﹐使用它的主焦点时通常至少需加入一块改正透镜或反射镜。
焦点。这种望远镜的主﹑副镜形状很接近旋转双曲面﹐在实用上可把这种系统近似地视为消除三级球差和彗差的﹑由旋转双曲面组成的系统。由于消除了彗差﹐可用视场比其他形式的卡塞格林望远镜更大一些﹐并且像斑呈对称的椭圆形。如果采用弯曲底片﹐视场会更明显地增大﹐像斑则呈圆形。一个主镜相对口径为1/3﹑系统相对口径为1/8﹑且像成在主镜后面不远处的这种望远镜﹐其主镜偏心率接近于1.06的双曲面﹐副镜偏心率接近于2.56的双曲面。在理想像平面(近轴光的像平面)上﹐如要求像斑的弥散不超过1﹐可用视场直径约为19'﹔如用弯曲底片﹐仍要求像斑的弥散不超过1﹐则视场直径可达37'。如要获得更大的视场﹐则需加入像场改正透镜。加入像场改正的R-C望远镜比主镜为抛物面的卡塞格林望远镜的效果也更好。但在R-C望远镜中使用主焦点时﹐所成的像是有球差的。因此﹐使用它的主焦点时通常至少需加入一块改正透镜或反射镜。
典型的卡塞格林系统主镜为抛物面,次镜为双曲面,这样只能校正球差,如果将主镜也改为双曲面则可以校正两种像差,球差和慧差,视场也可适当增大,但为了进一步增大视场则还需校正场曲、象散和畸变,这就还需要在像方加一组至少由两片透镜组成的校正透镜组,可称之为场镜。
(达--客 卡塞格林)
达尔-奇克汉卡塞格林望远镜是霍勒斯达尔在1928年设计出来的,并在1930年由 当时的科学美国人编辑,也是业余天文学家的艾伦奇克汉和艾伯特G.英格尔写成论文发表在该杂志上。这种设计使用凹的椭圆面镜做主镜,凸的球面镜做第二反射镜。这样的系统比卡塞格林或里奇-克莱琴的系统都容易磨制,但是没有修正离轴的彗形像差和视场畸变,所以离开轴心的影像品质便会很快的变差。但是对长焦比的影响较小,所以焦比在f/15以上的反射镜仍会采用此种形式的设计。
当时的科学美国人编辑,也是业余天文学家的艾伦奇克汉和艾伯特G.英格尔写成论文发表在该杂志上。这种设计使用凹的椭圆面镜做主镜,凸的球面镜做第二反射镜。这样的系统比卡塞格林或里奇-克莱琴的系统都容易磨制,但是没有修正离轴的彗形像差和视场畸变,所以离开轴心的影像品质便会很快的变差。但是对长焦比的影响较小,所以焦比在f/15以上的反射镜仍会采用此种形式的设计。
(H-C系统,霍顿卡塞格林):两个球面反射镜
Hougton的改正镜由一块双凸透镜和一块双凹镜组成,能很好的修正球差,彗差,畸变,可 用视场很大,色差也极小,可以忽略不计.像差主要是离轴像散,所有面都是球面,曲率半径较大(不象马克苏托夫的改正镜曲率半径很小)容易加工.对材料要求也较低. 安装方面,改正镜两透镜之间的间隔,以及和主镜间的距离的容差很大,主要是对正光轴.
用视场很大,色差也极小,可以忽略不计.像差主要是离轴像散,所有面都是球面,曲率半径较大(不象马克苏托夫的改正镜曲率半径很小)容易加工.对材料要求也较低. 安装方面,改正镜两透镜之间的间隔,以及和主镜间的距离的容差很大,主要是对正光轴.
Hougton用于目视和摄影都有很好的表现. 个人感觉Hougton做成大焦比(快速)用于摄影更能体现它的优势. 如果小焦比目视的话,和抛物面牛反相比基本没明显的优势,已有一些国外DIYer做出Hougton-牛望远镜. 这种形式可以说是目前DIYer唯一能自制的折反镜了. 另外,在oslo里测试过,当口径较小时(比如100mm,120mm),将改正镜的双凸透镜改为凸平镜,双凹镜改为凹平镜,虽然会引入一些像差,但是非常小(按摄影要求).只要要求不是相当的高,完全在可以接受的范围内.。施密特-卡塞格林式
施密特-卡塞格林式望远镜是一种折反射望远镜,以折叠的光路与修正板结合,做成一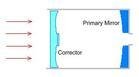 个紧密的天文学仪器。施密特-卡塞格林的设计是以伯恩哈德·施密特的施密特摄星仪为基础,一如施密特摄星仪使用
个紧密的天文学仪器。施密特-卡塞格林的设计是以伯恩哈德·施密特的施密特摄星仪为基础,一如施密特摄星仪使用 球面镜做主镜,并以施密特修正板来改正球面像差;承袭卡塞格林的设计,以凸面镜做次镜,将光线反射穿过主镜中心的孔洞,汇聚在主镜后方的焦平面上。有些设计会在焦平面的附近增加其他的光学元件,例如平场镜。
球面镜做主镜,并以施密特修正板来改正球面像差;承袭卡塞格林的设计,以凸面镜做次镜,将光线反射穿过主镜中心的孔洞,汇聚在主镜后方的焦平面上。有些设计会在焦平面的附近增加其他的光学元件,例如平场镜。
它有许多的变形(双球面镜、双非球面镜、或球面镜与非球面镜各一),可以被区分为两种主要的设计形式:紧密的和非紧密的。在紧密的设计中,修正板靠近或就在主镜的焦点上;非紧密的修正板则靠近或就在主镜的曲率中心上(焦距的两倍距离)。紧密设计的典型例子就是Celestron和Meade的产品,结合一个坚固的主镜和小而曲率大的次镜。这样虽然牺牲了视野的广度,但可以让镜筒缩成很短。多数紧密设计的Celestron和Meade的主镜焦比是f/2,而次镜是负f/5,产生的系统焦比是f/10。须要提出的例外是Celestron的C-9.25,主镜的焦比是f/2.3,次镜的焦比是f/4.3,结果是镜筒比一般紧密型的要长,而视野比较平坦。非紧密的设计让修正板靠近或就在主镜的曲率中心上,一种非常好的施密特-卡塞格林设计例子是同心,就是让所有镜面的曲率中心都在一个点上:主镜的曲率中心。在光学上,非紧密型的设计比紧密形的能产生较好的平场和变型的修正,但镜筒在长度上却有所增加。
马克苏托夫-卡塞格林式:
马克苏托夫是折射反射(面镜-透镜)望远镜,被设计来减少离轴的像差,例如彗形像差。在1944年,苏联光学家德密特利·马克苏托夫发明此型望远镜,在设计上以球面镜作主镜并结合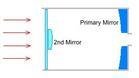 在入射光孔的弯月形的修正壳以改正球面像差,这是在反射望远镜和其他类型上的重大问题。马克苏托夫式的最大缺点是不能制作大口径的(>250毫米/10 英吋),因为受到修正板的抑制,重量和制作成本都会上扬。
在入射光孔的弯月形的修正壳以改正球面像差,这是在反射望远镜和其他类型上的重大问题。马克苏托夫式的最大缺点是不能制作大口径的(>250毫米/10 英吋),因为受到修正板的抑制,重量和制作成本都会上扬。
马克苏托夫物镜不能校正整个光束的球差,只能校正边缘球差,因此存在剩余球差,对轴外像差来说,只能校正慧差,不能校正象散。在他发明之际,马克苏托夫自己暗示有可能取代卡塞格林式的"折叠"光学的构造。珀金埃尔默的设计师约翰·葛利格里由马克苏托夫的想法发展出了马克苏托夫-卡塞格林望远镜。稍后,葛利格里在1957年的天空和望远镜杂志上发表了划时代的f/15和f/23的马克苏托夫-卡塞格林望远镜设计,为珀金埃尔默明确的预告了这项设计在商业上的用途。
许多被制造的马克苏托夫式都采用了"卡塞格林"的设计(有时称为斑点马克苏托夫 ),原本的次镜被在修正板内侧的一小片铝制的斑点所取代。好处是已经固定住无须再对正与校准,也消除了蜘蛛型支撑架所产生的衍射条纹。缺点则是损失了一定量的自由度(次镜的曲率半径),因为次镜的曲率半径必须与弯月形修正板的内侧一致。葛利格里自己,第二次,再设计的速度较快的(f/15)时,就改采修正板的前面或主镜为非球面镜来减少像差。
),原本的次镜被在修正板内侧的一小片铝制的斑点所取代。好处是已经固定住无须再对正与校准,也消除了蜘蛛型支撑架所产生的衍射条纹。缺点则是损失了一定量的自由度(次镜的曲率半径),因为次镜的曲率半径必须与弯月形修正板的内侧一致。葛利格里自己,第二次,再设计的速度较快的(f/15)时,就改采修正板的前面或主镜为非球面镜来减少像差。
施密特弯月形卡塞格林
这种类型的望远镜可谓是集合了施密特和马克苏托夫的优点,相当于是叫了两种校正器,施密特用于校正球差,弯月用于校正慧差,不过这种类型的卡塞格林长度显得有些过长,不适合大口径的使用。
阿古诺夫-卡塞格林
阿古诺夫-卡塞格林望远镜的设计是在1972年由P.P. 阿古诺夫首度介绍给世人的。他所有的光学元件都是球面镜,并将传统卡塞格林式的次镜换成三个有空气隙的透镜元件。距离主镜最远的透镜是曼京镜,它的作用如同第二个镜子的表面,在对向天空的一面有反射用的涂层。阿古诺夫的系统只使用球状的表面,避免了非球面的制造和测试。然而,获得的好处似乎很少,因为这套系统实际上非常难以制做,它需要精确的自由区域球的曲率半径以取代等效的非球面镜。
普雷斯曼-卡米歇尔卡塞格林
相比上述几种类型卡塞格林来说,Pressmann-Camichel Type最容易制造,但品质 较差,需加施密特校正器才能使用。
较差,需加施密特校正器才能使用。
"离轴"或"斜反射"反射镜卡塞格林:
Schiefspiegler("离轴"或"斜反射")反射镜 是一种非常奇特的卡塞格林反射镜,他将主反射镜倾斜以避免第二反射镜在主镜上造成阴影。虽然消除了衍射的图形,却又导致了其他不同的像差必须要修正。
是一种非常奇特的卡塞格林反射镜,他将主反射镜倾斜以避免第二反射镜在主镜上造成阴影。虽然消除了衍射的图形,却又导致了其他不同的像差必须要修正。
三反卡塞格林
三反射镜系统由三片反射镜组成,有两个间距、三个半径和三个圆锥系数共八 个变量,除了满足系统焦距、球差、彗差、像散、场曲等系统性能和像质要求外,还有足够的变量进行系统布局和结构的优化设计。三反射镜系统比两反射镜系统的视场大,且易于控制光学系统的杂散辐射,增加了轴外视场的光通量,使得像面照度更加均匀。随着空间技术的发展,全反射式光学系统,尤其是三反射式光学系统正在逐渐成为空间光学系统的主要形式。
个变量,除了满足系统焦距、球差、彗差、像散、场曲等系统性能和像质要求外,还有足够的变量进行系统布局和结构的优化设计。三反射镜系统比两反射镜系统的视场大,且易于控制光学系统的杂散辐射,增加了轴外视场的光通量,使得像面照度更加均匀。随着空间技术的发展,全反射式光学系统,尤其是三反射式光学系统正在逐渐成为空间光学系统的主要形式。
