在文章开始之前的，小编先给大家加整理了一份关于压缩模量的相关规范汇总，让大家先对这一块的知识能有一个大体上的了解。先通过对规范有一定的认识和理解，能更好的读懂下面文章正文的内容！

点击小程序，直接查看！

【提要】本文分析了土的压缩模量、变形模量的物理含义和物理关系，提出了根据砂土、碎石土等粗粒土承载力特征值进行其压缩模量估算的方法。

1、前言

在地基变形计算中，常常遇到砂土、碎石土等粗粒土地层，通常，对于粘性土、粉土来说，其压缩模量的取值可以根据其取样固结试验曲线，按照实际压力段，进行取值[1]。但对于砂土、碎石土等粗粒土来说，往往因为勘察阶段未进行取样固结试验，不能像粘性土、粉土一样，根据其固结试验曲线，按照实际压力段进行压缩模量取值。有时，勘察报告也同步给出了砂土、碎石土等粗粒土的压缩模量计算值（经验值），按其计算地基变形，有些时候，感觉计算结果不符合实际，遇到这种情况，着实为难了岩土工程师。为此，本文开展分析，提出根据砂土、碎石土等粗粒土承载力特征值进行估算其压缩模量的做法，供工程师缺乏其他有效办法时参考使用。

2、均质各向同性弹性体的应力应变关系和土的压缩模量与变形模量的理论关系回顾

对于均质各向同性弹性体，土的三维应力应变关系为：

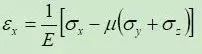
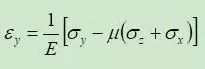
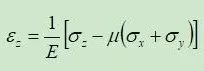
式中，E、μ表示弹性模量和泊松比。

应用于标准固结试验，有：

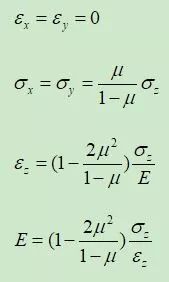
土具有弹塑性，将土的三维变形弹性模量称为变形模量E0，固结试验一维变形弹性模量称为压缩模量Es，由此得到压缩模量Es和变形模量E0的理论关系为：

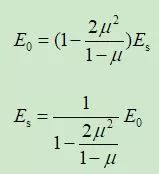
从上述理论表达式看出，变形模量E0在数值上一般应小于压缩模量Es的数值，但根据文献[2]，变形模量E0在数值上却是压缩模量Es数值的（3~5）倍。

3、估算粗粒土压缩模量Es的方法建议

按照弹性力学，圆形面积（直径为d）上的均布荷载p，其作用下中心点的沉降量s的表达式为：

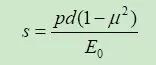
而圆形面积（直径为d）刚性板，在平均荷载pav作用下的平均沉降量s的表达式为：

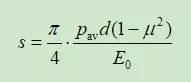
目前，规范给出的圆板载荷试验变形模量E0的计算公式，均采用了后者。但从上述刚性、柔性两种荷载作用下的沉降量看，差了π/4，即0.785倍。

综上，可以得出，依据载荷试验换算压缩模量的计算公式：

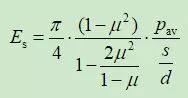
式中，s表示沉降量，d表示圆形板的直径，pav表示板下平均压力（压强），μ表示泊松比。

将上式中的pav改写为(fa-f0)，fa表示含深度效应的地基承载力特征值，f0表示自重压力，得到：

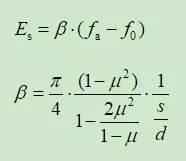
据文献[3]，建议泊松比μ的取值，碎石土0.27，砂土0.3。s/d取0.015，按照上式计算β值如下：

碎石土：β=60

砂土：β=64

4、算例

（1）碎石土

碎石土的地基承载力特征值fak为300kPa，埋深10m，上覆土的重度为19kN/m³，f0=190kPa，经深度修正后的承载力特征值fa为1094kPa，取μ=0.27，s/d=0.015，代入上式计算得到β=60，Es=60×(fa-f0)=60×(1094-190)=54240 kPa=54.2 MPa

（2）中砂

中砂的地基承载力特征值fak为200kPa，埋深8m，上覆土的重度为19kN/m³，f0=152kPa，经深度修正后的承载力特征值fa为827kPa，取μ=0.3，s/d=0.015,代入上式计算得到β=64，Es=64×(fa-f0)=64×(827-152)=43200 kPa=43.2 MPa

5、结束语

本文针对粗粒土的压缩模量的估算，在进行理论分析的基础上，给出了一个建议办法，期望工程师拿在不出其他更有效的办法情况下，参考使用，并积累经验。

参考文献

[1] 王长科. 《岩土工程勘察报告》提供压缩模量Es值要这样做. 微信公众平台《岩土工程学习与探索》，2017-11-07

[2] 高大钊. 土质学与土力学. 人民交通出版社，2001

[3] 国家标准. 岩土工程勘察规范(GB50021-2001)

文章转载自岩土工程学习与探索

完