本期题目如下：

如下图所示，有一个正方形ABCD。在BC和CD边上各取一点M和N，使得CM+CN等于正方形的边长AB。连接AM，连接AN，再连接对角线BD，BD与AM和AN分别相交于点P和Q。P和Q分对角线BD为三段BP、PQ和QD。试证明BP、PQ和QD三条线段一定可以构成一个三角形，并且这个三角形中一定有一个角等于60度。

证明：

本题采用把这个平面图形放入空间中的方法来证明比较简单和直观。我们作一个正方体，让这个正方形为正方体的一个面，比如让它成为正方体的上面。如下图所示。

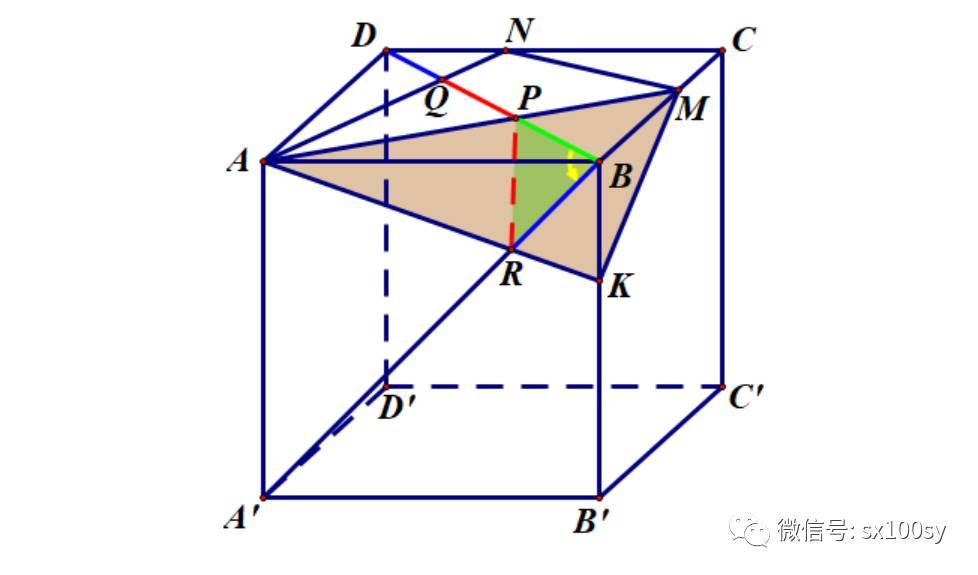
首先，在棱BB'上取点K，使BK=DN。连接AK，连接A'B，两线交于点R。连接PR。我们于是在空间中得到一个三角形BPR。我们只需要证明这个三角形的三条边长度就是BP、PQ和QD的长度。显然，BP没有问题。下面先来证明标蓝色的BR=QD。

因为BK=DN，所以，三角形ABK全等于三角形ADN。而A'B和BD是两个全等正方形的对角线，所以，BR=QD是显然的。

下面只需再证明两条红色线段相等，即证明PR=PQ。因为直角三角形BMK与直角三角形CMN全等，所以有MK=MN。再来观察三角形AMK与三角形AMN。显然，它们的三组对应边分别相等，所以它们全等，所以角PAR=角PAQ。而AR=AQ，所以，三角形APR全等于三角形APQ。所以PR=PQ。

上面过程，我们在空间中找到了一个三角形，它的三边长度就是对角线BD被分成的三段的长度，所以，本题结论成立。

另外，因为正方体任意两条相交于顶点的面对角线的夹角是60度，所以三角形BPR中的角PBR=60度，所以BP被分成的三段构成的三角形一定有一个角是60度。

答案是今天的日期21，也是“数学欣赏”系列的第21篇。