数学教学研究本公众号内容均由邵勇本人独创，可以转发，但转载则需获得邵勇本人的授权。每周推送两到三篇内容上有分量的数学文章，但在行文上力争做到深入浅出。几分钟便可读完，轻松学数学。

我们先来看平面上两个维度互相垂直且单位相同的网格。如下图所示。其中OA和OB为单位长度，OA垂直于OB，OA等于OB。

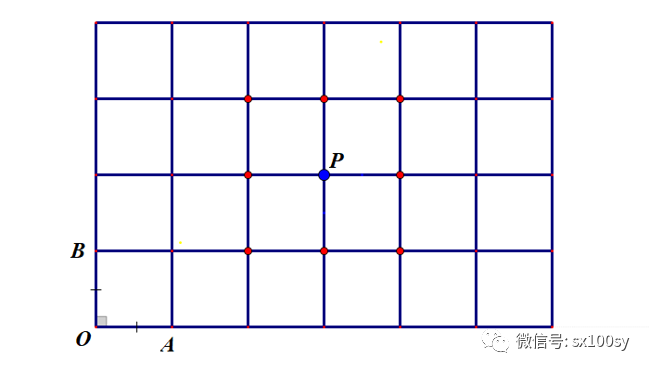
在网格中任意取一个格点（比如点P）。在任意一个格点的周围都有八个格点（比如上图中点P周围那八个红色的格点）。下面我们要寻找一个区域，让这个区域中的每一点到点P的距离都不大于它到点P周围8个点的距离。

我们知道，到两个定点的距离相等的点的轨迹就是以这两个点为端点的线段的中垂线。那么，到一个点的距离不大于到另一点的距离的点的全体构成的区域，就应该是被这条中垂线分成的两个半平面中，包含这个点的那个半平面（包括中垂线本身）。具体来说，如下图所示，包含点P的绿色半平面，就是到点P的距离不大于到点Q的距离的所有点构成的区域。

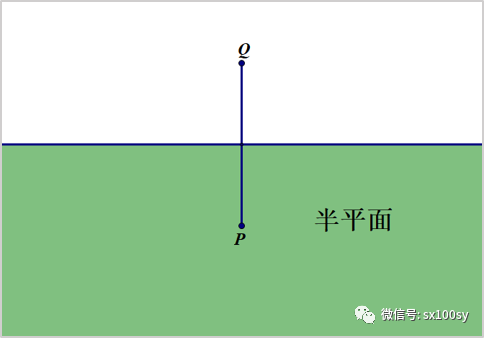
设所求区域为∑。于是，如下图所示，作出所求区域的步骤如下：

（1）分别连接点P与它周边的八个点：D、E、F、G、H、K、M、N，得到八条线段PD、PE、PF、PG、PH、PK、PM、PN。

（2）取这八条线段的中点，比如PM的中点为Q，PK的中点为R，PN的中点为S。

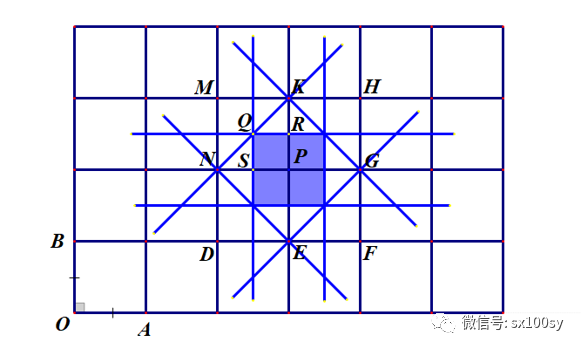
（3）过每条线段的中点作这条线段的垂线，得到八条直线（图中蓝色直线）。

（4）这八条直线围出来的区域就是所求的区域∑。如下图中的蓝色区域。它是一个正方形区域（包括边界和内部）。点P是它的中心。显然，这个正方形区域是可以铺满整个平面而不留任何空隙且互不重叠（以后称作满铺）。

上面的图形我是用数学软件绘制的。用鼠标选中点B，然后按住键盘上向上剪头键“↑”，从而点B向上移动，这使得纵轴上的刻度加大，即OB大于OA。但OB仍是与OA垂直的。那么，我们所求的区域会是什么样子的呢？很明显，应该是下图所示的样子。这是个长方形区域（包括边界及其内部）。这个矩形也是可以满铺整个平面的。

是不是觉得上面两种情况下，四条斜线没有起到什么作用？但不要着急，请继续往下看。如下图所示。这是在正方形网格的基础上，使两个维度的夹角不为90度。但两个维度上的刻度仍然相等，即OA=OB。

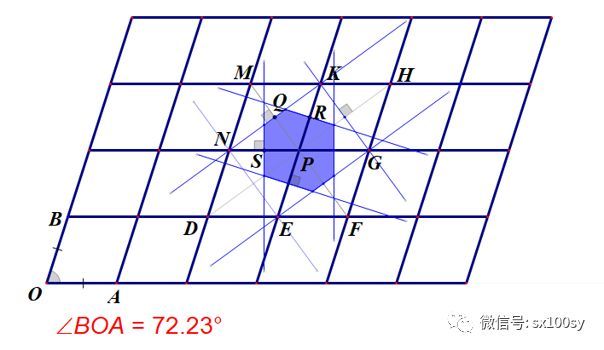
上图中∠BOA大约等于72度。我们再如第一种情况时那样，作出八条直线（连接点P与周围八个点的线段的中垂线），它们围出一个图形（这里虽然实际上起作用的只是六条直线，但作出八条直线是必须的）。围出来的图形是一个对边互相平行且相等的六边形。由于OA=OB的缘故，可以继续得出这个六边形有两组对边的长度是相等的，另一组对边的长度则不同。与PM和PF垂直的那两条互相平行的对边的长度与其他对边不同。

如果在上图情况的基础上，把夹角调整为60度（OA仍然等于OB），则这个六边形将成为正六边形。

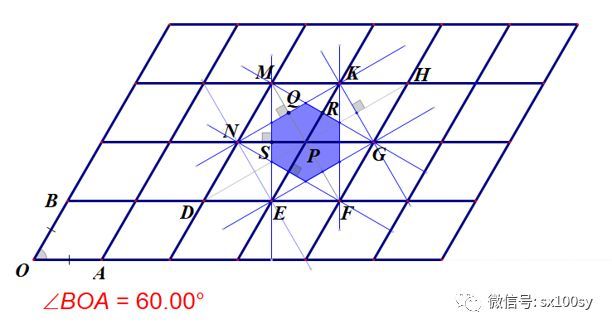
最后，我们把上上图调整为OA不等于OB，角BOA当然也不要等于60度。这是最一般的情形。于是所得六边形就是一个对边互相平行且相等的六边形。每组对边都相等，但互相之间一般不相等。如下图所示。

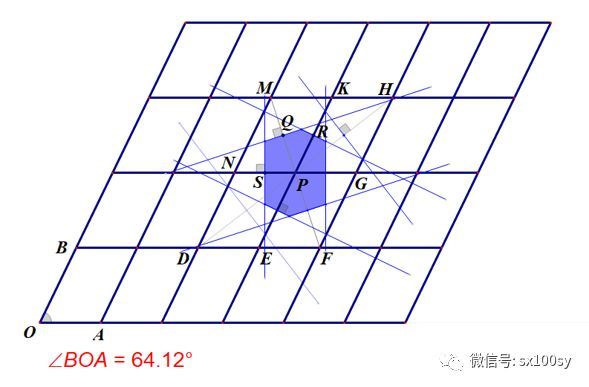
我们一共讲了五种情况，它们通称为狄利赫莱域（ Dirichlet Domain ）。

上面做了这么多事情，为了什么呢？意义何在？意义就是：这种六边形无数多个，是可以无缝隙无重叠地铺满整个平面的。前面的正六边形、正方形和长方形都是它的特殊情形。您可能会问，这有什么用？我首先要回答：不知道什么时候就会有用！数学研究的是事情的本质，然后才是实际用途。然后我要回答说，上述研究在壁纸或布匹的设计中，将发挥重要作用，因为您不可能亲手去画整面壁纸。你一定是设计好其中的一部分，然后复制到整张壁纸或整块布料上。

我们可以在一个这样的六边形中任意画出一个图案，那么，无数多个这样的六边形图案拼满整个平面后，就会出现意想不到的整体效果。设计师可以懂一些我这里讲的内容。下图是我随意设计的。您找一找原来的六边形在哪里。我随意画的，肯定画的很不好，应该把六边形的边界去掉，结果会更加连续。您可以设计得更好，可以充分发挥自己的想像力。再有，您一定见过埃舍尔的画吧，您也可以试一试。

自然会想到把平面情况拓展到空间。空间情况会复杂很多。以后讲。