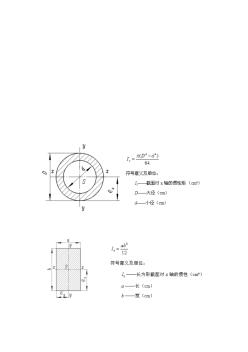
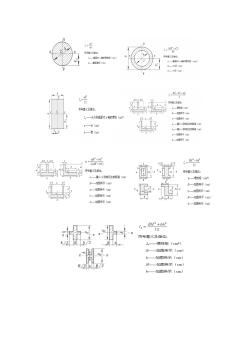
实心、空心及圆环形惯性矩与抗弯截面系数
2025-03-07
梁的强度条件 1. 纯弯曲梁的最大弯曲正应力: (1) 等截面直梁,中性轴为横截面对称轴 Wz—— 抗弯截面系数 (2) 中性轴不是横截面对称轴,且材料拉压强度不相等 (3) 利用正应力的强度条件可以对梁进行三种不同形式的强度计算: (a) 校核强度 (b) 选择截面尺寸或型钢号 (c) 确定许可荷载 2. 横力弯曲的梁 注意: (1) 一般的梁, 其强度主要受到按正应力的强度条件控制, 所以在选择梁的截面尺寸或确定 许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。 (2) 在弯矩为最大的横截面上距中性轴最远点处有最大正应力; 在剪力为最大的横截面的中 性轴上各点处有最大切应力。 轴惯性矩及抗弯截面系数 (1) 实心矩形的惯性矩及抗弯截面系数 (2) 空心矩形的惯性矩及抗弯截面系数 (3) 实心圆截面的惯性矩及抗弯截面系数 (4) 空心圆截面的惯性矩 三角形 bh 惯
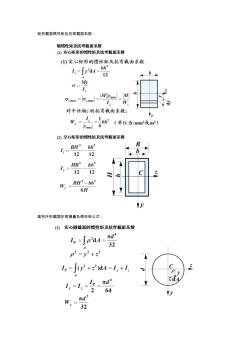
矩形截面惯性矩及抗弯截面系数: 圆形环形截面抗弯模量及惯性矩公式: 抗扭截面系数:

梁的强度条件 1.纯弯曲梁的最大弯曲正应力: (1)等截面直梁,中性轴为横截面对称轴 wz——抗弯截面系数 (2)中性轴不是横截面对称轴,且材料拉压强度不相等 (3)利用正应力的强度条件可以对梁进行三种不同形式的强度计算: (a)校核强度 (b)选择截面尺寸或型钢号 (c)确定许可荷载 2.横力弯曲的梁 注意: (1)一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定 许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。 (2)在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中 性轴上各点处有最大切应力。 轴惯性矩及抗弯截面系数 (1)实心矩形的惯性矩及抗弯截面系数 (2)空心矩形的惯性矩及抗弯截面系数 (3)实心圆截面的惯性矩及抗弯截面系数 (4)空心圆截面的惯性矩
编辑推荐下载

梁的强度条件 1.纯弯曲梁的最大弯曲正应力: (1)等截面直梁,中性轴为横截面对称轴 wz——抗弯截面系数 (2)中性轴不是横截面对称轴,且材料拉压强度不相等 (3)利用正应力的强度条件可以对梁进行三种不同形式的强度计算: (a)校核强度 (b)选择截面尺寸或型钢号 (c)确定许可荷载 2.横力弯曲的梁 注意: (1)一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定 许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。 (2)在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中 性轴上各点处有最大切应力。 轴惯性矩及抗弯截面系数 (1)实心矩形的惯性矩及抗弯截面系数 (2)空心矩形的惯性矩及抗弯截面系数 (3)实心圆截面的惯性矩及抗弯截面系数 (4)空心圆截面的惯性矩

两构件惯性 中心间距 x(cm) 单位长度重量 g1(kg/m) 截面积s1 (cm2) 惯性矩 i1(cm 4 ) 单位长度重量 g2(kg/m) 截面积s2 (cm2) 惯性矩 i2(cm 4 ) 偏心距 x1(cm) 2.751.96252.55.20835.88757.50.156252.0625 15202006666.6710100833.3335 4.2851.52265.0241207.3611.775150.450.7962 #div/0! #div/0! #div/0! #div/0! #div/0! #div/0! #div/0! #div/0! 两构件合二为一后,惯性矩的合并的计算 偏心距 x2(cm) 合并后惯性 中心的惯性 矩i0(cm 4) 0.687519.5442375 1022500 3.483801
热门文档 实心、空心及圆环形惯性矩与抗弯截面系数

截面的几何性质 15-1(i-8)试求图示三角形截面对通过顶点a并平行于底边bc的轴的惯性 矩。 解:已知三角形截面对以bc边为轴的惯性矩是,利用平行轴定理,可求得 截面对形心轴的惯性矩 所以 再次应用平行轴定理,得 返回 15-2(i-9)试求图示的半圆形截面对于轴的惯性矩,其中轴与半圆 形的底边平行,相距1m。 面对其底边的惯性矩是,用解:知半圆形截 平行轴定理得截面对形心轴的惯性矩 再用平行轴定理,得截面对轴的惯性矩 返回 15-3(i-10)试求图示组合截面对于形心轴的惯性矩。 解:由于三圆直径相等,并两两相切。它们的圆心构成一个边长为的等边三 角形。该等边三角形的形心就是组合截面的形心,因此下面两个圆的圆心,到形 心轴的距离是 上面一个圆的圆心到轴的距离是。 利用平行轴定理,得组合截面对轴的惯性矩如下: 返回 15-4(i-

1/14 惯性矩的计算方法及常用截面惯性矩计算公式 截面图形的几何性质 一.重点及难点: (一).截面静矩和形心 1.静矩的定义式 如图1所示任意有限平面图形,取其单元如面积da,定义它对任意轴的 一次矩为它对该轴的静矩,即y ydadsx xdadsy xda 整个图形对y、z轴的静矩分别为x×cy a ay ydasx xdas (i-1)0ayx 2.形心与静矩关系图i-1 设平面图形形心c的坐标为cczy,则0 a s yx, a s x y (i-2) 推论1如果y轴通过形心(即0x),则静矩0ys;同理,如果x轴 通过形心(即0y),则静矩0sx;反之也成立。 推论2如果x、y轴均为图形的对称轴,则其交点即为图形形心;如果 y轴为图形对称轴,则图形形心必在此轴上。 3.组合图形的
精华文档 实心、空心及圆环形惯性矩与抗弯截面系数
混凝土路缘石主要力学性能之一抗折强度的计算公式,涉及到较为复杂的形心矩、惯性矩及截面模量的计算。一般计算时都简化截面,导致误差较大,然而即使简化截面后的计算也相当繁琐。笔者介绍了运用autocad软件计算路缘石截面的惯性矩及截面模量的方法。
从塑料双壁波纹管环刚度的定义出发,针对广泛生产的梯形波纹状pe/pvc塑料双壁波纹管,运用cad软件分析管道纵截面的惯性矩,从而计算其环刚度。并与实验测试所得的环刚度进行比较分析后,运用vc++软件开发出塑料双壁波纹管的环刚度检验系统。
最新文档 实心、空心及圆环形惯性矩与抗弯截面系数
目的建立环形截面部分预应力混凝土高耸结构截面延性系数的精确计算公式,提出延性系数和预应力度的关系.方法根据周边均匀配筋的环形截面的受力特点和平截面假定,应用规范中混凝土和钢筋的常用应力应变关系,进行了环形截面部分预应力压弯构件的承载力和延性系数计算.结果提出了部分预应力压弯构件延性系数的计算公式、建立了延性系数和预应力度的关系曲线,为构件的设计和计算提供了参考.结论通过实例计算可以看出,随着预应力度的增加构件的延性系数降低很快,因此在进行部分预应力构件设计时,延性问题应该引起足够的重视.
分析研究了具有空心圆形截面圆钢拱的平面内非线性性能。提出了一些设计参数,如边界条件,矢跨比和夹角对强度的影响。此外,还讨论了其他一些因素,如几何和材料非线性,初始缺陷的影响。文中提供了分析拱非线性性能的预测标准和计算其非线性屈曲荷载的公式。分析发现:初始缺陷对强度的影响主要取决于拱的柔度和缺陷尺度,当拱圈深度越大,这种相关性就越小。几何非线性的影响,主要取决于拱的深度和柔度。短粗的拱较之长细拱受到矢跨比的影响要小一些。边界条件的影响极大程度上取决于浅拱的程度和柔度。细长拱较之短粗拱其强度退化更快。
本文介绍了门架形格栅的理论计算,并在支护结构的安全和经济方面与圆环形格栅进行了比较,认为门架形格栅比圆形格栅优越。
首先根据乌曼斯基第二理论,给出了三种闭口薄壁箱梁截面的扭转惯性矩简化计算方法,并重点介绍如何利用ansys自定义截面方法计算薄壁杆件的截面扭转惯性矩,最后通过实际算例分析了三种简化计算结果和ansys计算结果的差别,并且通过计算不同网格长宽比下的自由扭转惯性矩,指出网格长宽比对薄壁箱梁截面自由扭转惯性矩的精度影响规律。
为建立frp-混凝土-钢双壁空心管(简称双壁空心管)截面轴力-弯矩相关曲线方程,推导了双壁空心管压弯构件截面承载力计算公式,计算结果与试验结果符合较好。对构件的纤维特征值、内层钢管强度和含钢率等因素对双壁空心管截面轴力-弯矩关系的影响进行了分析。基于理论分析和试验结果,提出了双壁空心管截面轴力-弯矩相关曲线方程。

对于采用变截面支腿的水电站门式起重机,在计算大车架内力时常把大车架分成主门架、侧门架和水平框架按平面框架计算内力。对于变截面支腿,用力法计算平面框架内力时要先计算折算惯性矩。本文以莫尔位移公式和辛普生数值积分公式为依据,推导了某段变截面支腿的侧门架折算惯性矩。
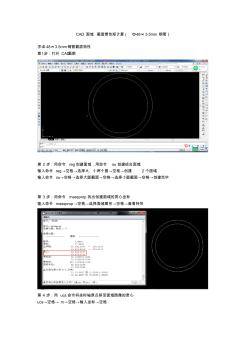
cad面域截面惯性矩计算(φ48×3.5mm钢管) 求φ48×3.5mm钢管截面特性 第1步:打开cad画图 第2步:用命令reg创建面域,用命令su创建组合面域 输入命令reg→空格→选择大、小两个圆→空格→创建2个面域 输入命令su→空格→选择大圆截面→空格→选择小圆截面→空格→创建完毕 第3步:用命令massprop找出创建面域的质心坐标 输入命令massprop→空格→选择面域图形→空格→查看特性 第4步:用ucs命令将坐标轴原点移至面域图像的质心 ucs→空格→m→空格→输入坐标→空格 第5步:输入命令massprop→空格→选择面域图形→空格→查看特性 第6步:计算截面的抵抗矩 wx1=惯性矩ix÷边界框y的一个值 wx2=惯性矩ix÷边界框y的另一个值 wy1=惯性矩iy÷边界框x的一个值 w
文辑创建者
我要分享 >
职位:房产估价师
擅长专业:土建 安装 装饰 市政 园林
相关编辑
文辑推荐
知识推荐
百科推荐