public class AVLTree<T extends Comparable<? super T>> {
private AVLNode<T> root;
public AVLTree() {root = null;}
/*** Check if given item x is in the tree.*/
public boolean contains(T x) {return contains(x, root);}
/*** Internal method to check if given item x is in the subtree.*
* @param x* the given item to check.
* @param t* the node that roots the subtree.*/
private boolean contains(T x, AVLNode<T> t) {while (t != null)
{int compareResult = x.compareTo(t.element);
if (compareResult < 0)
t = t.left;
else if (compareResult > 0)
t = t.right;
else
return true;}
return false;}
/*** Insert a new item to the AVL tree.*
* @param x
* the item to insert.*/
public void insert(T x) {
root = insert(x, root);}
/*** Internal method to insert into a subtree.*
* @param x
* the item to insert.
* @param t
* the node that roots the subtree.
* @return the new root of the subtree.*/
private AVLNode<T> insert(T x, AVLNode<T> t) {
if (t == null)
return new AVLNode<T>(x);
int compareResult = x.compareTo(t.element);
if (compareResult < 0)
{t.left = insert(x, t.left);
if (height(t.left) - height(t.right) == 2)
if (x.compareTo(t.left.element) < 0)
t = rotateWithLeftChild(t);
else
t = doubleWithLeftChild(t);}
else if (compareResult > 0)
{t.right = insert(x, t.right);
if (height(t.right) - height(t.left) == 2)
if (x.compareTo(t.right.element) > 0)
t = rotateWithRightChild(t);
else
t = doubleWithRightChild(t);}
else;
t.height = Math.max(height(t.left), height(t.right)) + 1;
return t;}
/*** Return the height of root t, or -1, if null.*
* @param t
* an AVLNode.
* @return the height.*/
private int height(AVLNode<T> t) {
return t == null ? -1 : t.height}
/*** Single rotation (left-left). Update height, then return new root.*/
private AVLNode<T> rotateWithLeftChild(AVLNode<T> z) {
AVLNode<T> y = z.left;
z.left = y.right;
y.right = z;
z.height = Math.max(height(z.left), height(z.right)) + 1;
y.height = Math.max(height(y.left), z.height) + 1;
return y;}
/*** Single rotation (right-right). Update height, then return new root.*/
private AVLNode<T> rotateWithRightChild(AVLNode<T> z) {
AVLNode<T> y = z.right;
z.right = y.left;
y.left = z;
z.height = Math.max(height(z.left), height(z.right)) + 1;
y.height = Math.max(height(y.right), z.height) + 1;
return y;}
/*** Double rotation (left-right).*/
private AVLNode<T> doubleWithLeftChild(AVLNode<T> z)
{z.left = rotateWithRightChild(z.left);
return rotateWithLeftChild(z);}
/*** Double rotation (right-left).*/
private AVLNode<T> doubleWithRightChild(AVLNode<T> z) {
z.right = rotateWithLeftChild(z.right);
return rotateWithRightChild(z);}
/**Remove item x.*/
public void remove(T x)
{root = remove(x, root);}
/*** Remove item x from subtree t.
* @param x the item to be removed.
* @param t the node that roots the subtree.
* @return the new root of the subtree.*/
private AVLNode<T> remove(T x, AVLNode<T> t) {
if (t == null)
return t;
int compareResult = x.compareTo(t.element);
if (compareResult < 0) {
t.left = remove(x, t.left);
if (height(t.right) - height(t.left) == 2)
if (height(t.right.left) < height(t.right.right))
t = rotateWithRightChild(t);
else
t = doubleWithRightChild(t);}
else if (compareResult > 0)
{t.right = remove(x, t.right);
if (height(t.left) - height(t.right) == 2)
if (height(t.left.left) > height(t.left.right))
t = rotateWithLeftChild(t);
else
t = doubleWithLeftChild(t);}
else if (t.left != null && t.right != null)
{t.element = findMin(t.right).element;
t.right = remove(t.element, t.right);
if (height(t.left) - height(t.right) == 2)
if (height(t.left.left) > height(t.left.right))
t = rotateWithLeftChild(t);
else
t = doubleWithLeftChild(t);}
else
{t = (t.left != null) ? t.left : t.right;}
if (t != null)
t.height = Math.max(height(t.left), height(t.right)) + 1;
return t;}
public T findMin()
{if (isEmpty())
return null;
return findMin(root).element;}
private AVLNode<T> findMin(AVLNode<T> t) {
while (t.left != null)
t = t.left;
return t;}
public T findMax()
{if (isEmpty())
return null;
return findMax(root).element;}
private AVLNode<T> findMax(AVLNode<T> t) {
while (t.right != null)
t = t.right;
return t;}
public void makeEmpty()
{root = null;}
public boolean isEmpty()
{return root == null;}
/** Internal class AVLNode */
private static class AVLNode<T>
{T element;
AVLNode<T> left;
AVLNode<T> right;
int height;
public AVLNode(T element)
{this(element, null, null);}
public AVLNode(T element, AVLNode<T> left, AVLNode<T> right)
{this.element = element;
this.left = left;
this.right = right;
this.height = 0;}}}
AVL
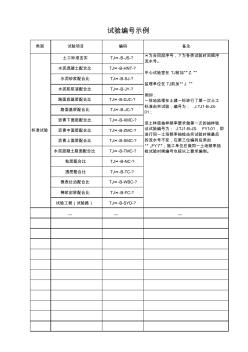单元划分及试验资料编码示例(定稿)
“数字化城管”之城市市政综合监管信息系统单元网格划分与编码规则
AVL树特点