阿基米德螺线
- 阿基米德螺线(亦称等速螺线),得名于公元前三世纪希腊数学家阿基米德。阿基米德螺线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹。阿基米德在其著作《螺旋线》中对此作了描述。
-

选择特殊符号
选择搜索类型
请输入搜索

阿基米德螺线的极坐标方程式为:
其中 a 和 b 均为实数。当
阿基米德螺线的平面笛卡尔坐标方程式为:
通用的从极坐标系到笛卡尔坐标系的变换方法:
通用的从笛卡尔坐标系到极坐标系的变换方法:
根据最新的研究表明,阿基米德螺旋公式可以用指定的半径r,圆周速度v,直线运动速度w来表示,公式为
根据这一公式,当圆周速度与直线速度同时增大一倍时,阿基米德螺旋的形状是不会发生变化的,因此,阿基米德螺旋属于等速度比螺旋,同时由于它在每个旋转周期内是等距离外扩的,故又可称它为等距螺旋 。
阿基米德螺旋的切线角度没有特定的规律,通过数学软件,按照求导数的方法,每隔45°做切线,会得到如图1的效果。
1.阿基米德螺线的几何画法
以适当长度(OA)为半径,画一圆O;作一射线OA;作一点P于射线OA上;模拟点A沿圆O移动,点P沿射线OA移动;画出点P的轨迹;隐藏圆O、射线OA&点P;即可得到螺线
2.阿基米德螺线的简单画法
有一种最简单的方法画出阿基米德螺线,用一根线缠在一个线轴上,在其游离端绑上一小环,把线轴按在一张纸上,并在小环内套一支铅笔,用铅笔拉紧线,并保持线在拉紧状态,然后在纸上画出由线轴松开的线的轨迹,就得到了阿基米德螺线。
为解决用尼罗河水灌溉土地的难题,阿基米德发明了圆筒状的螺旋扬水器,后人称它为“阿基米德螺旋”。
阿基米德螺旋是一个装在木制圆筒里的巨大螺旋状物(在一个圆柱体上螺旋状地绕上中空的管子),把它倾斜放置,下端浸入水中,随着圆柱体的旋转,水便沿螺旋管被提升上来,从上端流出。这样,就可以把水从一个水平面提升到另一个水平面,对田地进行灌溉。“阿基米德螺旋”扬水机至今仍在埃及等地使用。
阿基米德螺旋泵的工作原理是当电动机带动泵轴转动时,螺杆一方面绕本身的轴线旋转,另一方面它又沿衬套内表面滚动,于是形成泵的密封腔室。螺杆每转一周,密封腔内的液体向前推进一个螺距,随着螺杆的连续转动,液体螺旋形方式从一个密封腔压向另一个密封腔,最后挤出泵体。螺杆泵是一种新型的输送液体的机械,具有结构简单、工作安全可靠、使用维修方便、出液连续均匀、压力稳定等优点。
将一单盘蚊香光滑面朝上,放置一水平面上,自上俯视,会观察到的蚊香平面图。将这条曲线单独绘制出来,并加上一定的标志,得到了蚊香香条曲线图。点O为直线AB与曲线AB若干交点中位于最中间的一个交点。曲线OA实际上是单盘蚊香的香条外侧边线。观察不同厂牌蚊香的实物,会发现其对应的OA曲线上,接近点的一段,也就是所谓“太极头”部位的曲线,在形状上各有不同,但对于剩下的一大段曲线PA,则具有这样的特征:曲线PA E任取一点Q,假使点Q可在曲线PA上移动,则点Q越接近点A,点Q与点O的直线距离(以r表示)越大;而且,每移动一定角度(以θ表示),增加的值与该角度成正比。用数学语言描述曲线QA的上述特征,可表示为: △φ=k△θ,或
式(1)中,k和C均为恒定常数,若以点O为极点,建立极坐标,则选择适当方位的极轴,可以将式(1)转移为:
式(2)中α为点A,即香条末端对应的极角。式(2)所描述的曲线一单盘蚊香香条外侧边线.实际上正是“阿基米德螺线”。
需要说明的是,式(2)所描述的只是蚊香“太极头”之外的香条曲线方程,由于不同厂牌蚊香的“太极头”没有统一固定的形状,所以无法对其作出确切的描述。同时,由于“太极头”一段香条的长度极短,因而其形状对蚊香香条长度的影响事实上也可以忽略不计。

a=2;t=0:.1:20;r=a*t;polar(t,r)
阿基米德式螺旋机是阿基米德螺线的实际应用。关于阿基米德螺线在数学上的详细释义,请参见阿基米德螺线词条。
1.阿基米德螺线的几何画法以适当长度(OA)为半径,画一圆O;作一射线OA;作一点P于射线OA上;模拟点A沿圆O移动,点P沿射线OA移动;画出点P的轨迹;隐藏圆O、射线OA&点P;即可得到螺线...
极坐标方程式
它的极坐标方程为:r = aθ 这种螺线的每条臂的距离永远相等于 2πa。
笛卡尔坐标方程式为:
r=10*(1+t)
x=r*cos(t * 360)
y=r*sin(t *360)
z=0
阿基米德螺旋线的标准极坐标方程: r(θ)= a+ b(θ)
式中:
b-阿基米德螺旋线系数,mm/°,表示每旋转1度时极径的增加(或减小)量;
θ-极角,单位为度,表示阿基米德螺旋线转过的总度数;
a-当θ=0°时的极径,mm。
改变参数a将改变螺线形状,b控制螺线间距离,通常其为常量。阿基米德螺线有两条螺线,一条θ>0,另一条θ<0。两条螺线在极点处平滑地连接。把其中一条翻转 90°/270°得到其镜像,就是另一条螺线。
在极坐标系与平面直角坐标系(笛卡尔坐标系)间转换:
极坐标系中的两个坐标 r 和 θ 可以由下面的公式转换为直角坐标系下的坐标值(图一) 。 由上述二公式,可得到从直角坐标系中x 和 y 两坐标如何计算出极坐标下的坐标 (图二)。
在x=0的情况下:若y为正数,则θ=90°(π/2radians);若y为负,则θ=270°(3π/2radians).

阿基米德(约公元前287~前212),古希腊伟大的数学家、力学家。他公元前287年生于希腊叙拉古附近的一个小村庄。
公元前276年,也就是阿基米德十一岁时,阿基米德被父亲送到埃及的亚历山大城跟随欧几里得的学生埃拉托塞和卡农学习。亚历山大城位于尼罗河口,是当时世界的知识、文化贸易中心,学者云集,人才荟萃,被世人誉为“智慧之都”。举凡文学、数学、天文学、医学的研究都很发达。
阿基米德在亚历山大跟随过许多著名的数学家学习,包括有名的几何学大师—欧几里德,阿基米德在这里学习和生活了许多年,他兼收并蓄了东方和古希腊的优秀文化遗产,对其后的科学生涯中作出了重大的影响,奠定了阿基米德日后从事科学研究的基础。
公元前240年,阿基米德由埃及回到故乡叙拉古,并担任了国王的顾问。从此开始了对科学的全面探索,在物理学、数学等领域取得了举世瞩目的成果,成为古希腊最伟大的科学家之一。后人对阿基米德给以极高的评价,常把他和牛顿、高斯并列为有史以来三个贡献最大的数学家。
据说,阿基米德螺线最初是由阿基米德的老师柯农(欧几里德的弟子)发现的。柯农死后,阿基米德继续研究,又发现许多重要性质,因而这种螺线就以阿基米德的名字命名了。
与希皮亚斯割圆曲线相类似,可以用来化圆为方。不过,后者也是阿基米德自己完成的。如图2,螺线P=aθ的极点为O,第一圈终于点A。以O为圆心,a为半径作圆,则圆周长等于=OA。这样,阿基米德轻易解决化圆为方问题。
稍迟于阿基米德的阿波罗尼斯用圆柱螺线解决了化圆为方问题,如图2所示。设圆O是一直圆柱之底面,A是螺旋线之起始点。螺旋线在其上任一点P处的切线交底所在平面于T。则PT在底平面上的投影BT与AB相等。因此,当P点恰好为A点所在母线上离A最近的点时,TB与圆周长相等。从而化圆为方问题得以解决。
在阿波罗尼斯之后,机械师卡普斯(Carpus)也解过化圆为方问题。他所用的“双重运动曲线”今已失传,据数学史家唐内里(P. Tannery, 1843~1904)推测,它是摆线,亦即卡普斯是通过将圆沿直线滚动一周获得圆周长的(图3)。文艺复兴时期,意大利著名艺术大师达·芬奇(1452~1519)为化圆为方问题所吸引,并获巧妙方法。如图3,设圆半径为R,以圆为底作高为R/2的圆柱,然后将圆柱在平面上滚动一周,得矩形。将矩形化方,即完成化圆为方。
以上我们看到,希腊人很早就意识到(但未能证明)三大难题不能以尺规在有限步骤内完成。但它们看似如此简单,以至希腊人未能抵制诱惑;他们不断寻求尺规以外的方法,结果导致圆锥曲线、割圆曲线、蚌线、蔓叶线和螺线等高次曲线和超越曲线的相继发现。三大难题使一代又一代希腊数学家显示了非凡的聪明才智,并深刻影响了希腊几何的整个发展过程。
三大难题的魅力并未随希腊文明的沦亡而消失。事实上,从希腊以后特别是欧洲文艺复兴时期以来直到本世纪,对于它们的研究从未停止过。
1837年,年轻的法国数学家万采尔(P. L. Wantzel,1814~1848)证明了三等分角和倍立方尺规作图之不可能性。1882年,德国数学家林德曼(C. Lindemann, 1852~1938)证明了π的超越性,从而证明了化圆为方的尺规作图之不可能性。以后数学家们又还建立了两条一般定理:
定理1任何可用尺规由已知单位长度作出的量必为代数数;
定理2若一有理系数三次方程没有有理根,则它的根不可能用尺规由一给定单位长度作出。
自然界中,在千姿百态的生命体上发现了不少螺线。如原生动物门中的砂盘虫;软体动物门中梯螺科中的尖高旋螺,凤螺科中的沟纹笛螺,明螺科中的明螺,又如塔螺科的爪哇拟塔螺、奇异宽肩螺、笋螺科的拟笋螺等大多数螺类,它们的外壳曲线都呈现出各种螺旋状;在植物中,则有紫藤、茑萝、牵牛花等缠绕的茎形成的曲线,烟草螺旋状排列的叶片,丝瓜、葫芦的触须,向日葵籽在盘中排列形成的曲线;甚至构成生命的主要物质——蛋白质、核酸及多糖等生物大分子也都存在螺旋结构,如人类遗传基因(DNA)中的双螺旋结构。其中,自然界中的砂盘虫化石,蛇盘绕起来形成的曲线等都可以构成阿基米德螺线。
螺线之所以在生命体中广泛存在,是由于螺线的若干优良性质所确定。而这些优良性质直接或间接地使生命体在生存斗争中获得最佳效果。由于在柱面内过柱面上两点的各种曲线中螺线长度最短,对于茑萝、紫藤、牵牛花等攀缘植物而言,如何用最少的材料、最低的能耗,使其茎或藤延伸到光照充足的地方是至关重要的。而在各种曲线中,螺线就起到省材、节约能量消耗的作用,在相同的空间中使其叶子获取较多的阳光,这对植物光合作用尤为重要,像烟草等植物轮状叶序就是利用形成的螺旋面能在狭小的空间中(其他植物的夹缝中)获得最大的光照面积,以利于光合作用。形成螺线状的某些物体还有一种物理性质,即像弹簧一样具有弹性(或伸缩性)。在植物中丝瓜、葫芦等茎上的拟圆柱螺线状的触须就是利用这个性质,能使其牢固地附着其他植物或物体上。即使有外力(如风等)的作用,由于螺线状触须的弹性(或伸缩性),使得纤细的触须不易被拉断,并且当外力消失后,其弹性(或伸缩性)又能保证茎叶能恢复到原来的位置。螺旋线对于生活在水中的大多数螺类软体动物也是十分有意义的。观察螺类在水中的运动方式,通常是背负着外壳前进,壳体直径较粗大的部分在前,螺尖在后。当水流方向与运动方向相反时,水流沿着壳体螺线由直径较大的部分旋转到直径较小的部分直到螺尖。水速将大大减小,这样位于壳体后水的静压力将大于壳体前端的静压力。在前后压力差的作用下,壳体将会自动向前运动。这样一来,来自水流的阻力经锥状螺线的转化变为前进的动力。除此而外,分布在螺类外壳上的螺线像一条肋筋,大大增加了壳体的强度,也分散了作用在壳体上的水压。
螺线之所以在生命体中广泛存在,是由于螺线的若干优良性质所确定。而这些优良性质直接或间接地使生命体在生存斗争中获得最佳效果。由于在柱面内过柱面上两点的各种曲线中螺线长度最短,对于茑萝、紫藤、牵牛花等攀缘植物而言,如何用最少的材料、最低的能耗,使其茎或藤延伸到光照充足的地方是至关重要的。而在各种曲线中,螺线就起到省材、节约能量消耗的作用,在相同的空间中使其叶子获取较多的阳光,这对植物光合作用尤为重要,像烟草等植物轮状叶序就是利用形成的螺旋面能在狭小的空间中(其他植物的夹缝中)获得最大的光照面积,以利于光合作用。形成螺线状的某些物体还有一种物理性质,即像弹簧一样具有弹性(或伸缩性)。在植物中丝瓜、葫芦等茎上的拟圆柱螺线状的触须利用这个性质,能使其牢固地附着其他植物或物体上。即使有外力或风的作用,由于螺线状触须的伸缩性,使得纤细的触须不易被拉断,并且当外力(或风)消失后,保证其茎叶又能恢复到原来的位置。螺旋线对于生活在水中的大多数螺类软体动物也是十分有意义的。观察螺类在水中的运动方式,通常是背负着外壳前进,壳体直径粗大的部分在前,螺尖在后。当水流方向与运动方向相反时,水流沿着壳体螺线由直径大的部分旋转到直径小的部分直到螺尖。水速将大大减小,这样位于壳体后水的静压力将大于壳体前端的静压力。在前后压力差的作用下,壳体将会自动向前运动。这样一来,来自水流的阻力经锥状螺线的转化变为前进的动力。除此而外,分布在螺类外壳上的螺线像一条肋筋,大大增加了壳体的强度,也分散了作用在壳体上的水压。
阿基米德螺线 ,亦称"等速螺线"。当一点P沿动射线OP一等速率运动的同时,这射线有以等角速度绕点O旋转,点P的轨迹称为"阿基米德螺线"。
它的极坐标方程为:r = aθ
这种螺线的每条臂的距离永远相等于 2πa。
笛卡尔坐标
方程式为:
r=10*(1+t)
x=r*cos(t * 360)
y=r*sin(t * 360)
z=0
一动点沿一直线作等速移动的同时,该直线又绕线上一点O作等角速度旋转时,动点所走的轨迹就是阿基米德涡线。直线旋转一周时,动点在直线上移动的距离称为导程用字母S表示。
阿基米德涡线在凸轮设计、车床卡盘设计、涡旋弹簧、螺纹、蜗杆设计中应用较多。阿基米德涡线画法如图:
(1)先以导程S为半径画圆,再将圆周及半径分成相同的n等分,图中n=8;
(2)以O为圆心,作各同心圆弧于相应数字的半径相交,得交点Ⅰ、Ⅱ、Ⅲ、…Ⅷ各点,即为阿基米德涡线上的点;
(3)依次光滑连接各点,即得阿基米德涡线。
与希皮亚斯割圆曲线相类似,阿基米德螺线不但可以用来三等分角,也可以用来化圆为方。不过,后者也是阿基米德自己完成的。如图一,螺线P=aθ的极点为O,第一圈终于点A。以O为圆心,a为半径作圆,则圆周长等于=OA。这样,阿基米德轻易解决化圆为方问题。
稍迟于阿基米德的阿波罗尼斯用圆柱螺线解决了化圆为方问题,如图4-2-27所示。设圆O是一直圆柱之底面,A是螺旋线之起始点。螺旋线在其上任一点P处的切线交底所在平面于T。则PT在底平面上的投影BT与AB相等。因此,当P点恰好为A点所在母线上离A最近的点时,TB与圆周长相等。 从而化圆为方问题得以解决。
在阿波罗尼斯之后,机械师卡普斯(Carpus)也解过化圆为方问题。他所用的"双重运动曲线"今已失传,据数学史家唐内里(P. Tannery, 1843~1904)推测,它是摆线,亦即卡普斯是通过将圆沿直线滚动一周获得圆周长的(图二)。 文艺复兴时期,意大利著名艺术大师达·芬奇(1452~1519)为化圆为方问题所吸引,并获巧妙方法。如图4-2-29,设圆半径为R,以圆为底作高为R/2的圆柱,然后将圆柱在平面上滚动一周,得矩形。 将矩形化方,即完成化圆为方。
以上我们看到,希腊人很早就意识到(但未能证明)三大难题不能以尺规在有限步骤内完成。但它们看似如此简单,以至希腊人未能抵制诱惑;他们不断寻求尺规以外的方法,结果导致圆锥曲线、割圆曲线、蚌线、蔓叶线和螺线等高次曲线和超越曲线的相继发现。三大难题使一代又一代希腊数学家显示了非凡的聪明才智,并深刻影响了希腊几何的整个发展过程。
三大难题的魅力并未随希腊文明的沦亡而消失。事实上,从希腊以后特别是欧洲文艺复兴时期以来直到本世纪,对于它们的研究从未停止过。
1837年,年轻的法国数学家万采尔(P. L. Wantzel,1814~1848)证明了三等分角和倍立方尺规作图之不可能性。1882年,德国数学家林德曼(C. Lindemann, 1852~1938)证明了π的超越性,从而证明了化圆为方的尺规作图之不可能性。以后数学家们又还建立了两条一般定理:
定理1 任何可用尺规由已知单位长度作出的量必为代数数;
定理2 若一有理系数三次方程没有有理根,则它的根不可能用尺规由一给定单位长度作出。


 阿基米德蜗杆在UG中精确建模的研究
阿基米德蜗杆在UG中精确建模的研究
阿基米德蜗杆在UG中精确建模的研究
通过对阿基米德蜗杆的加工车刀和路线的数学分析,再在unigraphics当中仿照加工过程生成模型.并对生成的模型进行了数学理论和实际建模的外形校核.

 基于MasterCAM的阿基米德蜗杆三维设计
基于MasterCAM的阿基米德蜗杆三维设计
基于MasterCAM的阿基米德蜗杆三维设计
本文通过实例介绍阿基米德蜗杆的参数设计,并研究以MasterCAM软件为平台,根据设计的参数对阿基米德蜗杆进行三维建模。
阿基米德螺线是实践中常用的一种曲线。动点在一直线上做匀速运动,而这条直线又围绕着自己上面的一个定点作匀速转动的动点的轨迹称为阿基米德螺线,也叫等速螺线或平面螺线。它的极坐标方程为:
阿基米德在其《螺线》(On Spirals) 一书中引进了在极坐标ρ与θ之下的平面螺线ρ=aθ(如图3所示),其绕线不在同一平面上。据说,阿基米德螺线最初是由阿基米德的老师柯农(欧几里德的弟子)发现的。柯农死后,阿基米德继续研究,又发现许多重要性质,因而这种螺线就以阿基米德的名字命名了。为解决用尼罗河水灌溉土地的难题,它发明了圆筒状的螺旋扬水器,后人称它为“阿基米德螺旋”。除了杠杆系统外,值得一提的还有举重滑轮、灌地机、扬水机以及军事上用的抛石机等。被称作“阿基米德螺旋”的扬水机至今仍在埃及等地使用。一些喷淋冷却塔所用的螺旋喷嘴喷出喷淋液的运动轨迹也为阿基米德螺线。
对数螺线是一种特殊曲线。指在极坐标系中,极半径ρ的对数与极角θ的比为常数的点M(ρ,θ)的轨迹。它的极坐标方程为
从植物嫩枝的顶端往下,叶子大致上是按对数螺线排列的,这样能使采光面积达到最大;在古生物的研究中,也应用了这种曲线。对数螺线上任一点的切线,与切点的矢径相交成固定的角。这一性质在机械上有广泛的应用。如果旋转的切削刀沿此曲线的弧运动,就可保持固定的切削角,这种刀已在锄草机中使用。为了制造的方便,对数螺线的短弧,可以用阿基米德螺线的短弧近似代替。
双曲螺线,也称反螺线,是一种特殊曲线,是阿基米德螺线关于极点的反演图形。它是极径和极角成反比例的动点轨迹。双曲螺线的方程是:
双曲螺线
阿基米德螺线是实践中常用的一种曲线。动点在一直线上做匀速运动,而这条直线又围绕着自己上面的一个定点作匀速转动的动点的轨迹称为阿基米德螺线,也叫等速螺线或平面螺线。它的极坐标方程为:
阿基米德在其《螺线》(On Spirals) 一书中引进了在极坐标ρ与θ之下的平面螺线ρ=aθ(如图1所示),其绕线不在同一平面上。据说,阿基米德螺线最初是由阿基米德的老师柯农(欧几里德的弟子)发现的。柯农死后,阿基米德继续研究,又发现许多重要性质,因而这种螺线就以阿基米德的名字命名了。为解决用尼罗河水灌溉土地的难题,它发明了圆筒状的螺旋扬水器,后人称它为“阿基米德螺旋”。除了杠杆系统外,值得一提的还有举重滑轮、灌地机、扬水机以及军事上用的抛石机等。被称作“阿基米德螺旋”的扬水机至今仍在埃及等地使用。一些喷淋冷却塔所用的螺旋喷嘴喷出喷淋液的运动轨迹也为阿基米德螺线。
对数螺线是一种特殊曲线。指在极坐标系中,极半径ρ的对数与极角θ的比为常数的点M(ρ,θ)的轨迹。它的极坐标方程为
从植物嫩枝的顶端往下,叶子大致上是按对数螺线排列的,这样能使采光面积达到最大;在古生物的研究中,也应用了这种曲线。对数螺线上任一点的切线,与切点的矢径相交成固定的角。这一性质在机械上有广泛的应用。如果旋转的切削刀沿此曲线的弧运动,就可保持固定的切削角,这种刀已在锄草机中使用。为了制造的方便,对数螺线的短弧,可以用阿基米德螺线的短弧近似代替。
双曲螺线,也称反螺线,是一种特殊曲线,是阿基米德螺线关于极点的反演图形。它是极径和极角成反比例的动点轨迹。双曲螺线的方程是:
双曲螺线
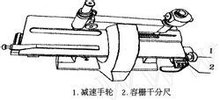
针对误差产生的原因,对原阿贝比长仪的一种改进。
⑴用容栅千分尺代替阿基米德螺线细分结构。
容栅千分尺读数可分辨到0. 1μm,如果通过合理的设计安排,利用容栅千分尺来代替阿贝比长仪,测微目镜中的光学放大加阿基米德螺线细分结构,就可以有效消除在前面关于比长仪主要仪器误差来源中提出的,由于物镜放大倍数不准及旋转分划板上阿基米德螺线偏心所引起的误差。
⑵对仪器分划板的改造
通过前面的改造,虽然完全消除了读数显微镜物镜放大倍数不准及阿基米德螺线偏心带来的误差,但判读方法并不理想,为了能更好地进行判读。参照原测微目镜固定分划板的尺寸,设计、改装了如图所示的分划板。
比长仪可以完全去掉结构复杂的测微目镜,故可大幅度降低仪器的制造成本。如果用一个放大倍率更大的目镜则可提高测量的判读精度(原仪器将读数显微镜目镜的倍率设计为5 倍,是为了有2 mm 的视场,改造后则无此要求)。通过容栅千分尺自带的串行通讯口,还可实现用计算机实时采集数据。