1 引言

20 世纪以量子力学和相对论为代表的物理学的革命，推动了化学、材料科学、生命科学等学科的飞速发展，还催生了以信息科学技术为标志的众多高新技术领域。特别是半导体工艺技术的成熟出现，人类进入了信息化时代，引起了人类社会科技、文化、经济、思想各个领域的翻天覆地的变革。可以说，当今信息科学的重要载体是微电子与光电产业。不断追求更高的品质永远是人类的目标。这一点在信息科技领域更加明显。从1980 年代商用计算机进入人们的日常生活以来，短短30 年间就经历了几代的历程。如此飞速发展的基础是微电子及光电子器件的不断小型化和高速化。

随着器件的不断小型化、高速化，微电子器件和正在发展中的纳米电子器件在很小的空间产生大量的热量。这些热量既来源于导线中的焦耳热，也包括电容的充放电过程中产生的热量。典型的集成电路芯片包含上百万个半导体晶体管。在现有的商用处理器中，散热是一个关键问题。常用的散热方法是对芯片本身进行整体散热。然而，随着三维芯片技术的发展，将产生更小和更热的热点。如图1(a)所示一个微处理器上的温度分布。虽然整体的温度并非很高，只有80 ℃ ，但局域高温区的温度可以超过110 ℃ 。温度升高会导致器件寿命缩短，可靠性大幅降低。此外，当前应用的散热片以及风扇降温的方法是对器件整体降温，因此制冷效果很差，同时也增加了能耗。美国能源部的数据统计，2006 年美国数据中心的能耗中， 超过50%的能源用于制冷系统(图1(b))，这反映了传统散热技术的局限。因此更高的散热效率成为微纳米信息技术进一步发展的关键技术。

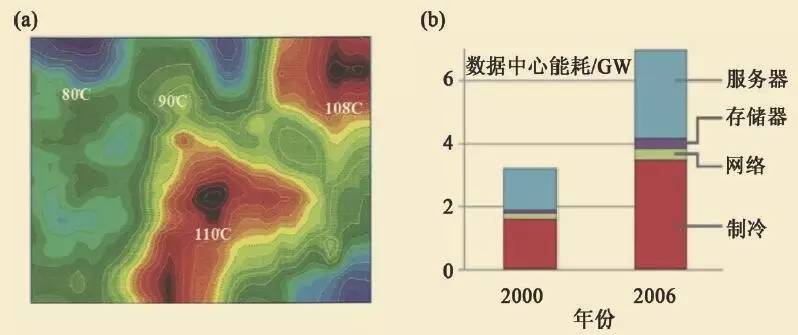
图1 (a)一个微处理器上的温度分布。绿色区域温度为80°C，红色区域温度为110°C；(b) 2006年美国的数据中心能耗分布。

解决微纳米器件的散热问题，需要我们对纳米尺度热传导的物理机制有全面深刻的理解。除应用方面的意义，这一问题的研究也对低维体系基本物理问题的发展有所贡献。近年来，基于实验技术的提高，一些新型的纳米体系已经可以构筑并直接测量，其中发现的新的物理机制、物理效应为相关学科的发展提供了坚实的基础，并为能源、信息等国民经济与国家安全的重要领域的突破提供了契机。热传导是自然界基本的能量传输形式之一。和电子、光子一样，声子也是能量的载体。相对材料的电子结构、电学输运性质的研究，人们对声子热传导的研究较少。除电学特性外，对于纳米科技的未来应用，其热学(声子态)性质也是极其重要的。

在本文中，我们以碳纳米管和石墨烯为例，介绍低维纳米体系热传导的新奇物理效应。同时，我们简单回顾了纳米器件发展的历程和现状。结合纳米器件的散热问题，讨论纳米材料热传导性质及其应用。目前，人们对纳米材料热传导性质较十年前已有了更多的了解。限于篇幅，我们这里只介绍碳纳米管及石墨烯的超高热导率的物理机制及应用。关于纳米体系热传导的更全面介绍，可参见相关综述文献。

2 纳米器件的发展历史与现状

2.1 半导体集成电路的发展回顾

1947 年发明的半导体晶体管以及随后于1958 年发明的半导体集成电路平面工艺，开启了基于半导体硅器件和芯片的信息科技时代的序幕。于1959 年正式进入商业化的半导体集成电路在发展了6 年之后，1965 年Farichild 半导体公司(Intel 公司前身)的创始人之一摩尔发现，大约每年在一块芯片上集成的单个单元器件数目翻一倍。根据这个规律摩尔博士预言：这个指数式的增长将使得10 年后的1975年，单个芯片上将有可能集成65000 个单元器件。事实上，在这个发展规律提出之后的将近50 年里，半导体硅芯片产业印证了这个伟大的猜想。虽然指数式发展趋势有一些小的修正，比如用晶体管数目代替每个芯片单元器件的计数来更好地反映互补金属氧化物半导体(complementary metal oxide semiconductor, CMOS)数字电路的发展，器件个数的倍增也减速为每18 个月翻一倍，但是基于不断进步的半导体工艺的硅芯片在性能和产量上确实保持了指数形式增长，并得到了史无前例的大发展，这个发现现在称为“摩尔定律”。回望过去，从1960年代到2000年代，实现一个晶体管的二进制开关所需要的电子数降低了5个数量级，同时，一个芯片上所集成的晶体管的数量提高了9 个数量级。现在的半导体硅集成电路芯片已经具有2 万亿美元的产业，发展成为世界上最大的工业产业之一。更强大、更便宜的半导体芯片作为经济加速器为每一个经济领域中的增产和发展创造了源源不断的动力，我们可以在现代生活的每一个层面找到它们的存在。

通过现代工艺对半导体器件微缩化，可以提高晶体管的集成密度、增进晶体管的运行性能同时减小其功耗。国际半导体技术路线图(ITRS)将摩尔定律总结为以器件特征尺寸为代表的每一代半导体工艺，设定在每一代技术中使得器件的电容C和电压V各减小到0.7。这就导致以下进步：(1)栅延迟(~CV/I)减小30%，同时运行频率(f~ I/CV)提高43%；(2)晶体管密度提高一倍； (3) 每个晶体管所消耗的能量(CV2)减小65%，功率(CVf2)减小50%，芯片的平均功率密度不变。这样摩尔定律从描述单位面积晶体管数目的增加，转变为更直观地描述器件特征尺寸的减小。直到集成电路进入130nm 工艺时， 晶体管的微缩化依然是简单地按比例减小氧化层的厚度、晶体管沟道的长度和宽度。这样在维持一个恒定的功率密度下，可以使得器件的运行速度得到相应的提升。这种在现有构架和材料下简单地微缩化器件本身称为“Dennard”微缩化方式。但是氧化层厚度的减小使得栅极的漏电流随之快速增加，芯片的发热成为一个极大的问题，一个典型的例子是2002 年英特尔奔腾4 处理器在冲击4GHz 主频时遭遇到了散热危机，于是这个“Dennard”微缩化方式在130nm工艺时不得不终止了。

为了克服这些实现“摩尔定律”的障碍，各种新材料和新构架被发展出来。以高介电质为代表的新材料和以应变沟道、金属源漏电极、金属栅电极为代表的新器件构造的新微缩化方案开始不断涌现，继续支持摩尔定律的延续，这被称为“更多摩尔”(more Moore)。正如摩尔博士所言“没有任何指数式增长是永恒的，但是我们可以让终结来得更迟一些”。这些新技术和新构架的引入使得硅工艺依然具有很大空间进行微缩化，随后90nm、65nm、45nm 工艺得以一一实现，2012 年32nm工艺即将完结，22nm 工艺即将导入，之后的20nm工艺正在开发中，更小线宽的工艺正在实验室中研发。ITRS 2011 版预言， 在不远的2020 年代， 我们将进入10nm 线宽时代，在那时，每个芯片中的晶体管数量将达到1万亿个的量级。

2.2 摩尔定律的极限

摩尔定律所预言的半导体集成电路器件的微缩化，给工业界指明了一个不断减小每个晶体管的成本、同时实现更强大的功能的可能。同时，研究者们也看到这个以指数式增长的趋势必将到达一个尽头，从理论上和实验上可以归纳为如下几项极限：

(1) 基础理论极限主要来自于热力学、量子力学、电磁学的物理规律。这些与具体的材料、系统、环境无关，是最本征的限定因素。热噪声(3/2)kBT 限制了在二进制中转换一个单电子需要的最小能量为(ln2)kBT，这里kB是玻尔兹曼常数，T是绝对温度。此外，电子具有波粒二相性，量子力学中的海森伯不确定性原理指出，在二进制体系中改变一个晶体管0/1 状态所需要的能量与所用时间的乘积必须大于或等于普朗克常数。在已知所需能量的情况下，这个关系实际上限定了器件所能达到的最快状态翻转速度。进一步，信号在芯片中点与点之间的信号延迟度，也就是芯片的整体运行速度也由光速最快的物理事实所限定。

(2) 材料极限。这与具体的材料有关，但是不依赖于器件结构特征和器件尺寸。比如击穿场强、电子饱和速度、热导率等。

(3)器件极限。包括漏电流、短沟道效应、掺杂起伏、内部连接R-L-C等。

(4)电路极限。包括内部连接负载、散热等。

这些最基本的物理极限不依赖于具体的材料性质、器件结构、电路构型、系统构架，被认为是未来万亿级别的集成电路之后的不可逾越的障碍。但是当我们仔细审视过去50 年的发展历程的时候可以看到，摩尔定律的经济基石是每个器件的最小成本，在同样面积的芯片上将每一个器件做得更小，将有效降低每个器件的平均成本。但是，事实上正如很多研究者和摩尔博士本人所认识到的那样，巨额的研发费用必须被投入到如何将器件做得更小的科研项目中，当这个费用已经接近甚至超出了器件微缩化所带来的商业利润时，可能就是摩尔定律终结之时，而这个时候我们也许离理论极限还很远。

2.3 超越摩尔定律：后摩尔时代

为了应对“摩尔定律”的终结，继续器件的微缩化，一些在传统器件和电路中还没有使用的自由度被加进来以开发新的功能器件，从而跳出摩尔定律的范畴，这被称为“超越摩尔”(more than Moore)。一个代表性的例子是，目前为止半导体集成电路仍然是以多数载流子(包括电子和空穴)输运特性为主。电子同时携带有电荷自由度(1.6×10-19C)和自旋自由度(±h/2p)。到目前为止的经典微电子学中, 电子的输运过程仅利用它的电荷自由度，并由电场来控制, 而它的自旋自由度是不予考虑的。随着器件特征尺寸的进一步减小，以至于固体器件中电子的德布罗意波长与这个特征尺寸可比拟时，许多宏观特性将丧失，进入纳米领域的集成器件不再遵从经典物理规律，而是具有显著的量子效应和统计涨落特性。特别是，当电子受到一维到多维的尺度限制的时候，经典电磁学理论不再适用，其传输特性完全由量子力学来决定。基于单电子库仑阻塞效应的单电子晶体管，具有明显的更小功耗，近期内得到了广泛重视，但是其较小的增益仍然有待解决。在更强的量子效应区域，电子的传输更加体现出多自由度的相互影响。研究纳米尺度和单分子条件下的电子传输，以及电子—电子、电子—声子、电子—光子、电子—自旋相互作用在电子输运上的体现，是目前纳米科技和凝聚态物理研究中最为前沿的课题之一。

2.4 纳米器件的能耗

纵观整个半导体硅集成电路的发展，虽然新材料、新构架、新器件、新设计不断涌现，摩尔定律依然有足够的空间发展到本世纪30 年代，之后的完全建立在全新规范上的信息处理技术也已经逐步成型，但是散热问题很早以前就被认识到可能成为信息处理技术的一个重要发展瓶颈。输入能量和将这个能量所转化的热能传导出去是制约信息处理科技性能的一对矛盾体。在数字电路CMOS单元中，能量被使用在了向电容的充放电过程中，这个过程所伴随的载流子在供电单元和地之间的流动将产生一定的热量。另外在集成电路中，层和层之间沟通各个单元之间的互联导线也会由于焦耳热作用产生热量。对于高端微电子芯片而言，其性能的充分发挥极大地受限于在不超过稳定运行温度时有多少热量能够被散发出去。对更高性能半导体微处理器芯片的追求已经导致了更高的器件集成度和更快的时钟频率，这产生了更多的热量。为了使这些芯片能够可靠地运行，对芯片的有效散热和制冷变得越发重要起来。另外，更多的集成层数、更快的运行时钟频率、更多的来自于内连线的发热、导入的更多新材料往往具有较差的导热性能，这些都给有效的热管理带来了极大的挑战。更快开关、更低功耗的晶体管总是依赖于特征尺寸减小所带来的供电电压的降低，但是热噪声的电压扰动并不会随着特征尺寸的减小而减小，在可以预见的十几年内，供电电压将会减小到这个热噪声极限。

为了更好地实现微纳米器件中的温度控制，需要我们对纳米尺度热传导的物理机制有全面深刻的理解。下面我们以碳纳米管和石墨烯为例，讨论纳米尺度中的反常热传导、反常热扩散等新奇物理效应。

3 碳纳米管的热传导

3.1 傅里叶定律

人们通常应用傅里叶定律来描述热传导问题。傅里叶定律的形式如下，

J =－k∇T，

其中J 为体系的热流密度，即单位时间通过单位面积的热量，∇T 为材料中的温度梯度，κ为材料的热导率(thermal conductivity)。傅里叶定律还可以写为另一种形式，即

Q =－λΔT，

这里Q 为流过的热流，ΔT 为两端温度差，λ为热导(thermal conductance)。从傅里叶定律可以看出，在系统两端温度差固定的情况下，材料热导率提高，能传导的热量也随之增加。因此，可以采用高热导材料来解决微纳器件散热的问题。

3.2 固体的声子热传导

声子是固体中原子实的振动(格波)的量子力学描述。固体中声子态与电子态决定了固体的几乎一切物理性质，是从微观层次了解固体性质，进而利用并加以改造的基础。固体中的声子分为声学声子和光学声子。声学声子是组成固体的最小可重复单元中的各个原子近似于以相同方向振动，它主要与物质的力学和声学性质有关。而光学声子是最小单元中的各个原子相对振动，主要与物质的光学性质有关。20世纪50年代，随着玻恩的声学声子的唯象理论以及后来被称为“黄昆方程”的一系列理论的建立，人们已经可以从微观的原子模型来得出固体的声学声子和光学声子的性质，以及声学波与电磁波的耦合。20 世纪80 年代，以“黄朱模型”为代表的半导体超晶格声子模式理论的发展，引发了一系列的理论和实验研究工作，有力推动了低维体系声子理论的深入研究。

和电子、光子一样，声子也是能量和信息的载体。已有研究表明，在室温下，碳纳米管和石墨烯等纳米材料中，声子对热导率的贡献起主要作用，决定了材料的热导率。因此这些材料是研究声子热传导的理想体系。

3.3 碳纳米管的反常热传导

碳纳米管和石墨烯是近年来的研究热点。石墨烯是具有六角网格结构的单原子层二维结构，碳纳米管则是碳原子组成的一维(准一维)结构。这两种碳基纳米结构具有强烈的关联。单壁碳纳米管可以认为是由单层石墨烯平面弯曲得到，而将单壁碳纳米管展开即可得到石墨烯纳米条带。实验发现，碳纳米管具有很高的室温热导率。Kim等人利用微加工技术，搭建了纳米热桥(thermal bridge)结构。通过测量温度差和热流，即可得到碳纳米管的热导率。他们发现，室温下，碳纳米管的热导率达到3000W/m·K，而在此之前有报道的热导率最高的材料是金刚石，其室温热导率也只有2000W/m·K。碳纳米管的高热导率使其迅速成为了研究的热点。而人们发现其热导率还有大幅度提高的空间。

对三维体材料来说，材料的热导率是一个只依赖材料成分和温度的本征参数，与材料的尺寸无关。而近年来的理论研究表明，这一在体材料中成立的基本规律，在低维纳米材料中不再成立。图2 给出了基于分子动力学计算得到的碳纳米管热导率随长度的变化关系。同样长度的情况下，碳纳米管的热导率随管径增加。更重要的是，对单壁碳纳米管，其热导率随长度增加而增加。如图2 所示，这里显示的是在双对数坐标下热导率随长度的变化， 为线性变化关系。因此对单壁碳纳米管，其热导率对长度的依赖关系为：k~Lβ。在室温下，对(5, 5)型单壁碳纳米管，β为0.40。并且该数值随温度及管径变化。管径增加以及温度升高，β减小。这是因为随温度升高，原子振动振幅加大，非线性效应更加明显，从而导致随温度升高而β 明显降低。

图2 碳纳米管热导率随长度的变化关系。

3.4 碳纳米管中反常热扩散

导致这种反常热传导现象的物理机制可通过研究热脉冲在碳纳米管中的传输来理解。如图3(a)所示，在初始时刻，碳纳米管处于300K温度的平衡态。此后在碳纳米管中部加一高温度脉冲，然后记录温度分布的扩散行为。研究表明，由于碳纳米管中的碳—碳键能很强，使得温度脉冲能够迅速扩散。为了定量研究扩散行为，可以定义温度脉冲的宽度为

这里Ei,t 是原子i 在时刻t的能量, ri,t是原子i在t时刻的位置， ri,0是原子i在初始时刻t=0的位置。

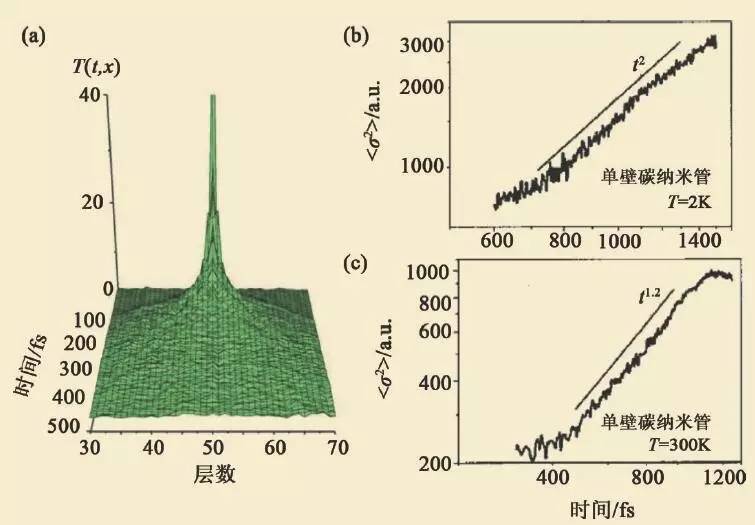
图3 (a)通过热脉冲在碳纳米管中的传输来理解(b)和(c)中不同温度下热脉冲宽度随时间的展宽

图3 给出了温度脉冲宽度随时间的展宽，可以用幂数关系<σ2> ∝ tα 描述，其中α为描述热扩散的主要参数。α =2 表示弹道输运，α >1 为超扩散(super-diffusive)，α=1 表示正常扩散，α <1 为亚扩散(sub-diffusive)。从图中可见，室温下碳纳米管中α =1.2，对应为超扩散。通过对不同低维体系进行系统的研究，Li和Wang提出了描述热传导和热扩散系数之间的关系公式：

β = 2 - 2/α。这个关系表明，α =1 时可得到b =0，表示正常扩散导致与尺寸无关的热导率，即我们通常所见的体材料的情况。而α >1 时，b >0，体系的热导率随尺寸发散，这也是我们所看到的碳纳米管中的情况。如果我们将这里计算得到的α=1.2 带入此式，可以得到β ≈ 1/3 ，和非平衡分子动力学直接计算得到的结果符合得很好。因此，碳纳米管中的反常热扩散是其热导率随尺寸变化的物理基础，解释了理论和实验观察到的碳纳米管热导率随长度增加的现象。

碳纳米管热导率随长度增加而增加的效应得到了加州大学伯克利分校实验的直接证实。如图4 所示，应用微纳加工技术，Chang 等人制备了可测量纳米尺度温度及热流的“热桥”平台，并应用这一测量平台研究了碳纳米管热导率随长度的变化关系。由图4(b)可见，他们的实验测量结果与傅里叶定律给出的变化关系差别很大，而与理论预言的指数发散符合得很好。由于在体材料中，从傅里叶定律得到的材料热导率只依赖材料的组分和温度，而与材料的尺寸、形状无关。因此在纳米材料中发现的热导率随材料尺寸而变化的现象被称为反常热导，在某些文献中也称傅里叶定律在纳米材料中不再成立。

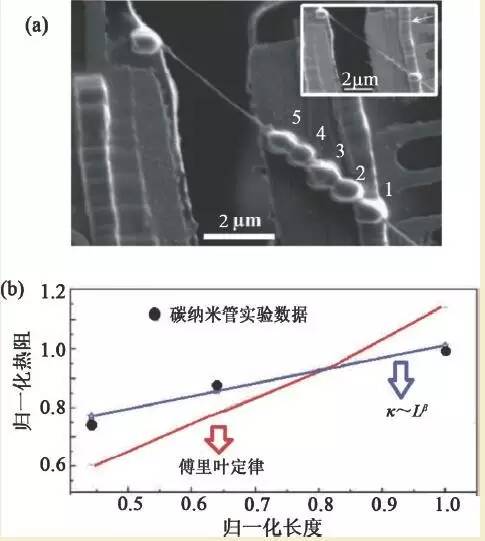
图4 (a)可测量纳米尺度温度及热流的“热桥”平台；(b)实验测量的碳纳米管热导率随长度的变化关系。

3.5 影响碳纳米管热导率的因素

以上我们讨论的是理想无缺陷、无杂质的完整碳纳米管的热传导性质。在实际情况中，碳纳米管可以存在杂质和缺陷， 这些都会降低碳纳米管的热导率。其中一种常见的杂质即同位素无序掺杂。图5 给出了在存在同位素掺杂情况下碳纳米管的热导率。随同位素掺杂浓度提高，热导率下降。在低同位素掺杂的情况下，热导率下降非常显著。仅20%的同位素掺杂即可降低热导率达50%以上。这一理论预测很快得到了加州大学伯克利分校Majumdar 教授研究组的实验证实。他们的实验测量结果和分子动力学的理论预言在定量上高度一致，即20%的同位素掺杂降低热导率达50%。此外，表面吸附以及晶格缺陷等也会显著降低碳纳米管的热导率。

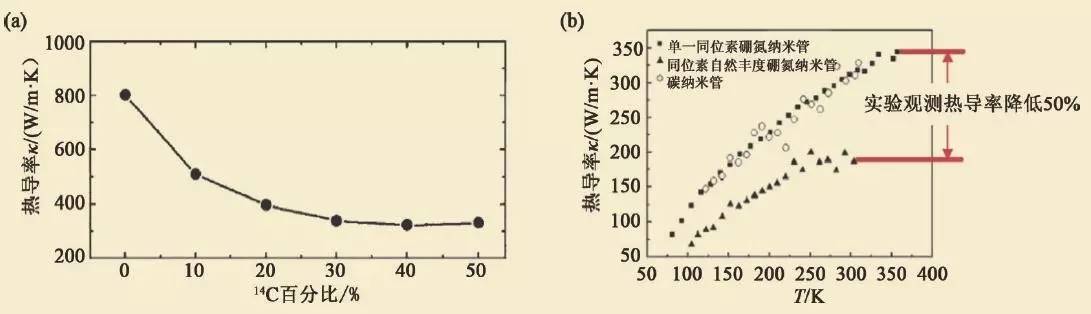
图5 存在同位素掺杂情况下碳纳米管的热导率(a)分子动力学模拟结果；(b)实验测量结果。

4 石墨烯的热传导性质

4.1 石墨烯的超高热导率

除碳纳米管外，石墨烯这种单原子层纳米材料的热学性质，也引起了人们极大的研究兴趣。石墨烯通常被定义为碳原子以sp2杂化结构连成的单原子层蜂窝状的结构。它是组成其他碳材料的基本单元，如图6 所显示的那样，石墨烯包裹起来可形成零维的富勒烯，卷起来可形成一维的碳纳米管，层层堆积则形成三维的石墨。不同于传统的二维体系，石墨烯费米面处能量的色散关系是线性的，而非传统的二维电子气中的抛物线型色散关系。独特的电子结构使得石墨烯具有极高的载流子迁移率和超长的平均自由程，是理想的电子材料。此外可以通过电子束刻蚀、化学反应等方法从石墨烯上裁剪出不同宽度和边界形状的准一维结构，即石墨烯纳米条带。根据石墨烯纳米带边界形状可以把它分为锯齿型边界纳米带和扶手椅型边界纳米带。研究表明，锯齿型边界纳米带是金属型，而扶手椅型边界纳米带依赖其宽度可以为金属型或半导体型。

图6 石墨烯形成零维富勒烯、一维碳纳米管及三维石墨的示意图

除新颖的电学性质，石墨烯还具有优异的热学性质。Balandin 等人实验发现， 石墨烯的室温热导率可以高达5300W/m·K， 远远高于金刚石的热导率。这是由于碳—碳原子间有着很强的共价键相互作用。此外，目前成熟技术制备的石墨烯也有着较好的晶格完整性，较少的缺陷散射也是其超高热导率的起因之一。

4.2 石墨烯热导率的尺寸效应

和碳纳米管热导率相似，石墨烯纳米带的热导率也依赖其尺寸。应用分子动力学计算，人们发现石墨烯纳米带的热导率随宽度增加而变化。如图7 所示，锯齿型边界纳米带热导率随宽度而增加，达到某一宽度后，随宽度继续增加而减小。与此不同的是，扶手椅型边界纳米带热导率随宽度单调增加。这是由于不同边界对声子散射产生的局域态不同而造成的。

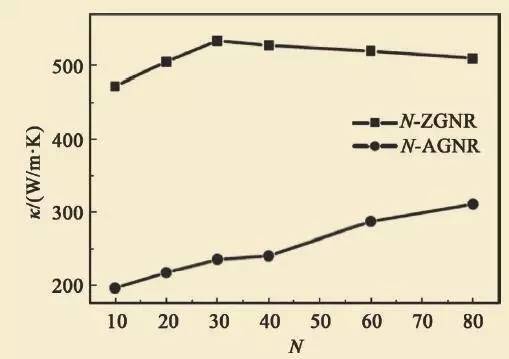
图7 石墨烯纳米带的热导率k 随宽度N的变化关系(图中ZGNR表示锯齿型边界纳米带，AGNR表示扶手椅型边界纳米带)。

应用以微纳米加工技术为基础的“热桥”测量平台，石墨烯纳米带热导率随长度及层数的变化也得到了实验的系统研究。图8 显示的就是这样的测量平台。从透射电子显微镜照片可见，实验平台分为左右两个部分，实验时石墨烯纳米带放置其上，中间可以悬空，以防止通过衬底的热流损失。实验中可以通过流过导线的电流给一侧加热，从而产生温度差。从流过的热流及两端的温度差，即可得到石墨烯纳米带的热导率。研究发现，对悬空多层石墨烯纳米带，热导率随长度增加而增加。然而由于单层石墨烯的柔性，使其很难悬空于衬底上，因此关于单层石墨烯纳米带热导率尺寸效应的实验研究还有待进一步的技术改进。

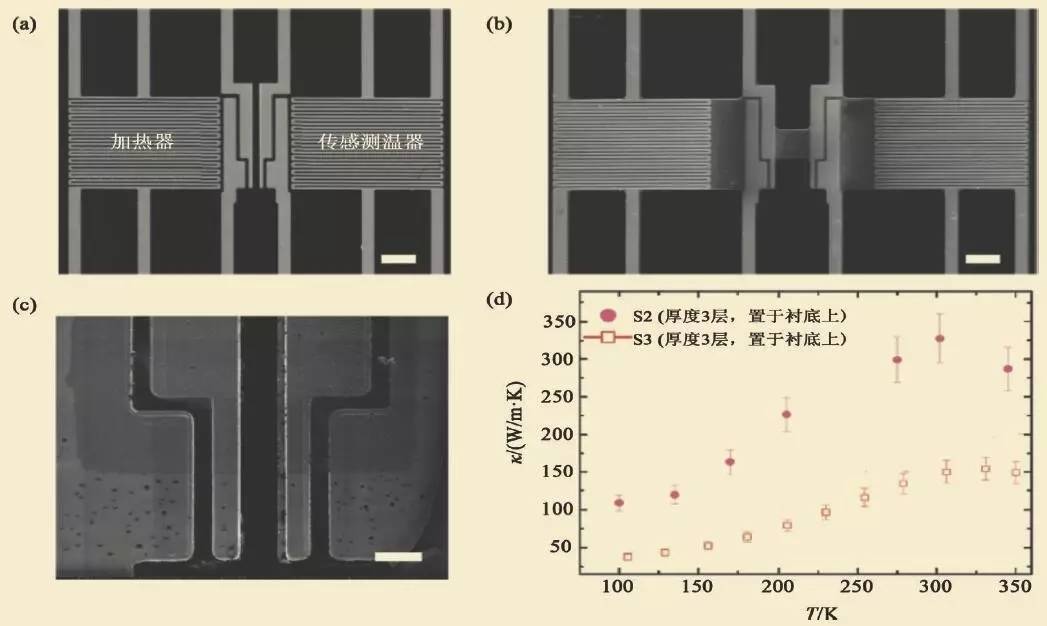
图8 (a)—(c)实验研究石墨烯纳米带热导率的“热桥”测量平台的透射电子显微镜照片；(d)石墨烯纳米带热导率随长度及层数的变化关系。其中样品S2 悬空部分长度为2mm ，样品S3 悬空部分长度为1mm。

4.3 影响石墨烯热导率的因素

各种因素对石墨烯纳米带热导率存在不同的影响。由于边界处存在未饱和键，边界化学吸附对热导率有很大的影响。此外，结构缺陷、空位和界面也都会不同程度地降低石墨烯纳米带的热导率。拉伸、压缩等形变对石墨烯纳米带的稳定性和热导率也有很大的影响。与单层石墨烯相比，多层石墨烯纳米带的热导率有很大不同。由于层间相互作用对声子输运产生额外的散射，因此多层石墨烯的热导率相对单层结构有明显的下降。此外，在实际应用中，石墨烯经常放置于衬底上。由于衬底的作用使得声子能带结构改变，影响了石墨烯纳米带中特定频率的声子散射。和电学性质相似，石墨烯纳米带的热导率也明显依赖于边界形状。如图9所示，室温下锯齿型边界纳米带热导率比扶手椅型边界纳米带热导率高30%。这种取向引起的差异随纳米带宽度增加而减小，当纳米带宽度超过100nm时，两者的热导率之间的差别可以忽略。

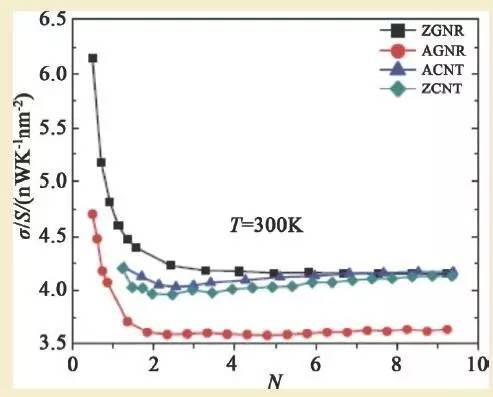
图9 室温下锯齿型边界(ZGNR)及扶手椅型边界(AGNR)纳米带热导率的比较(图中ZCNT 和ACNT 分别表示锯齿型边界及扶手椅型边界碳纳米管)。

4.4 石墨烯的可裁剪特性

与碳纳米管相比，石墨烯为柔性材料，具有很多独特的性质，例如其可裁减的特性。随着纳米加工技术的进步，人们可以通过电子束刻蚀、化学反应等方法对石墨烯进行可控裁减，从而有目的地获得需要的宽度和边界形状的石墨烯纳米条带。这些使得石墨烯成为实现声子器件功能的理想体系，可以构建不同的热控制器件，如热二极管等基本声子元件。应用计算模拟，人们研究了不同形状(如梯形(图10(a))、不同宽度纳米结(图10(b))、Y-型结构 (图10(c)))石墨烯纳米带的热整流效率。发现在这些非对称结构中，存在明显的非对称热流，即热整流效应。这些纳米材料中的热整流效应的发现，也激发了宏观体系相应的实验研究。最近，人们发现石墨烯纳米纸(reduced graphene oxide)的可裁剪性使其具备了实现宏观热整流的功能。如图10(d)所示，通过裁剪得到的宏观尺寸的非对称石墨纸，在“1”端加高温，“2”端加低温，得到的热流比相反温度梯度下的热流高20%。这种明显的热整流效果来源于非对称石墨纸中的温度不均匀分布以及这种新型材料对温度的高敏感依赖。

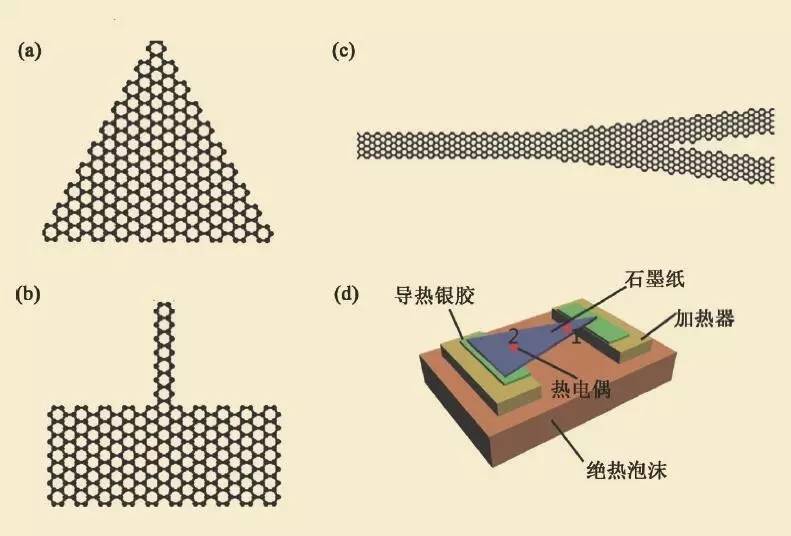
图10 (a)—(c)具有热整流效应的不同形状非对称石墨烯纳米带；(d)基于石墨烯纳米纸的宏观热二极管器件。

5 结束语

本文介绍了纳米尺度热传导研究中的一些基础物理问题，以及近年来该领域中一些热点研究方向和新奇物理机制。在过去的十年中，以新近涌现出的碳纳米管和石墨烯等为代表的低维体系受到广泛重视。研究这些系统本身的热传导特性，不仅具有基本的基础理论意义，对于深入理解包括非线性、能量扩散在内的基本物理原理具有重要意义；而且与当前可再生能源以及微纳电子器件进入原子尺度后发展所要求更高的集成度和处理速度密切相关，具有广阔深远的应用前景。现有的微电子器件和正在发展中的纳米电子器件在很小的空间产生大量的热量。随着三维芯片技术的发展，将产生更小和更热的热点。因此，更高的散热效率成为纳米功能器件进一步发展的关键。而碳纳米管和石墨烯的高热导率可以有助于将产生的热量传导出去，从而提高器件的可靠性和寿命。对低维体系热传导的深入研究，必将对未来的科技、经济乃至社会生产力的发展产生划时代的影响。

近年来，中国科学家在纳米尺度热传导的理论、计算模拟以及实验研究方面获得了一系列进展，已成为国际上这一领域不可或缺的重要力量。纳米功能器件中的温度控制是未来全世界共同面临的严重问题，已经成为世界各国迫切需要解决的关键技术。深刻认识纳米材料中热传导的物理机制，并在此基础上优化发展新材料体系是该领域基础研究的核心问题。整体上讲，纳米尺度热传导是新兴学科，各国几乎同时起步，我们完全可以抓住机遇，发展具有自主知识产权的新方法、新技术和新理论，为国内相关学科领域的国家重大研究提供支持，为我国科研事业和国民经济的可持续发展做出贡献。

本文选自《物理》2013年第2期

十大热门文章

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

END