Introduction
(Students are required to know the study objects, contents and methods of Theoretical Mechanics and Mechanics of Materials.)
Introduction
01 Reductions of force systems
(Students should be able to understand the Principles of statics, how to reduce a concurrent force system to a single equivalent force, how to calculate the moment of a force about a point/axis and the concepts of couples, how to draw free-body diagrams, how to reduce an arbitrary force system to a force and a couple)
1.1 Fundamental concepts of statics
1.2 Basic operations with force systems
1.3 Support reactions and free-body diagrams
1.4 Reductions and resultants of force systems
Tests for week 1
02 Equilibrium of force systems
( Students should be able to perform equilibrium analyses of composite bodies and determine the unknowns in the structure,understand the role of friction in equilibrium analysis and solve some simple problems involving friction)
2.1 Coplanar equilibrium equations
2.2 Equilibrium of composite bodies
2.3 Plane truss analysis
2.4 Center of gravity and centroid
2.5 Friction
Tests for week 2
03 Kinematics of a point
(Students should know how to determine the position, velocity and acceleration of a point by the method of rectangular coordinates and the method of normal and tangential coordinates.)
3.1 Kinematics of a point
04 Translation and rotation of rigid bodies
(Students should understand the fundamental concepts of translation and rotation of rigid bodies.)
4.1 Translation and rotation of rigid bodies
05 Composite motion of a point
(Students are required to know the definition of absolute, relative and transport velocities (accelerations), and should be able to solve problems using theorem of composition of velocities (accelerations).)
5.1 Composite motion of a point (I)
5.2 Composite motion of a point (II)
Tests for week 3
06 Plane motion of rigid bodies
(Students should be able to perform velocity analysis by the base point method, theorem for projection of velocities and instantaneous center for velocities, and also acceleration analysis by the based point method.)
6.1 Plane motion of rigid bodies
6.2 Plane motion analysis (I)
6.3 Plane motion analysis (II)
Tests for week 4
07 Kinetics of a particle
(Students should know how to determine the force, acceleration or velocity of a particle by differential equations of motion.)
7.1 Kinetics of a particle
08 Principle of impulse and momentum
(Students are required to know the concepts about impulse and momentum and be able to solve kinetic problems using the principle of linear impulse and momentum and motion of the mass center for a system of particles.)
8.1 Principle of impulse and momentum (I)
8.1 Principle of impulse and momentum (II)
Test for week 5
09 Principle of angular impulse and momentum
(Students are required to know the concepts about angular impulse and angular momentum and be able to solve kinetic problems using the principle of angular impulse and momentum.)
9.1 Mass moment of inertia
9.2. Principle of angular impulse and momentum
10 Principle of work and kinetic energy
(Students should be able to solve kinetic problems using the principle of work and kinetic energy.)
10.1 Principle of work and kinetic energy
Test for week 6
11 D'Alembert's principle
(Students should know how to determine the inertial forces and inertial moments and be able to solve kinetic problems using D’Alembert’s principle.)
11.1 D'Alembert's principle
Test for week 7
12 Stress
(Students should be able to understand the method of section for internal force determination, the concepts of stress, gerneral stress state, average normal and shear stresses, and safety factor, the method to determine required cross section area or dimensions.)
12.1 Equilibrium of a deformable body
12.2 Stress
12.3 Average normal stress in an axially loaded bar
12.4 Average shear stress
12.5 Allowable stress
13 Strain
(Students should be able to understand the concepts of strain, normal strain, shear strain, general strain state and the assumpations for small strain analysis.)
13 Strain
Test for week 8
14 Mechanical properties of materials
(Students should understand the concepts related to stress-strain diagram, brittle and ductile materials, and Hooke's law.)
14.1 The tension and compression test
14.2 The stress-strain diagram
14.3 Stress-strain behavior of ductile and brittle materials
14.4 Hooke's law, Poisson's ratio, the shear stress- strain diagram
15 Axial load
(Students should be able to understand the concept of Saint-Venant's Principle, know how to determine the elastic deformation of an axially loaded bar and how to solve statically indeterminate problems.)
15.1 Saint-Venant's Principle, Elastic deformation of an axially loaded member
15.2 Elastic deformation of an axially loaded member (continued)
15.3 Principle of superposition, Statically indeterminate axially loaded member
15.4 Thermal stress, the stress on the inclined surface
15.5 Stress concentration
Test for week 9
17 Bending
(Students should be able to draw shear force and bending moment diagrams, know the sign conventions for shear force and bending moment, know the derivation of normal stress on the cross section of beam bending and the flexure formula.)
17.1 Shear and moment diagrams
17.2 Graphical method for constructing shear and moment diagrams
17.3 Bending deformation of a straight member
17.4 The flexure formula
Test for week 10
16 Torsion
(Students should know the shear stress distribution of a circular shaft and how to solve statically indeterminate problems for torque-loaded members.)
16.1 Torsional deformation of a circular shaft
16.2 The torsion formula
16.3 Angle of twist
16.4 Statically indeterminate torque-loaded members
18 Transverse shear
(Students should know the shear stress distribution in a beam with prismatic cross seection and the method to determine the shear stress and shear flow for beams or thin-walled members.)
18.1 Shear in straight members, the shear formula
18.2 Shear stresses in beams
19 Combined loadings
(Students should know how to determine the critical section and critical point of member under combined deformation.)
19.1 Thin-walled pressure vessels
19.2 State of stresses caused by combined loadings
test for week 11
20 Stress transformation
(Students should be familiar with the concepts of stress state, know how to perform plane-stress transformation, know how to perform stress state analysis by graphical method.)
20.1 Plane-stress transformation
20.2 Principal stresses and maximum in-plane shear stress
20.3 Mohr's circle-plane stress
20.4 Absolute maximum shear stress
21 Deflections of beams and shafts
(Students should be able to determine the deflection and slope of beams by the integration method and the superposition method, know to to solve statically indeterminate problems.)
12.1 The elastic curve
12.2 Slope and displacement by integration
12.3 Method of superposition, statically indeterminate beams and shafts
Test for Week 12

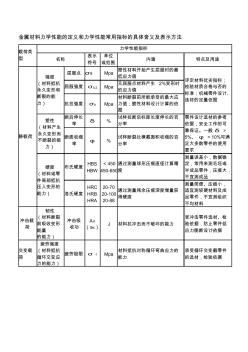 金属材料力学性能的定义
金属材料力学性能的定义

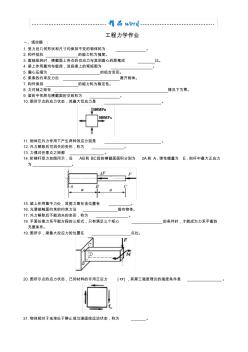 工程力学作业
工程力学作业