选择特殊符号

Ф δ ° × # Ⅱ Ⅲ ½ ¼

选择搜索类型

市场价信息价参考价询价供应商云知资讯文库百科

热门搜索

造价通

请输入搜索

首页 > 百科 > 建设工程百科

静电位能计算公式

静电位能计算公式

点电荷 在场中某点处的静电势能等于把它从该点移动到电势零点时电场力所作的功，即 为该点的电势。 对电荷体密度为 的电荷体系，它在外场中的静电势能为 静电势能是标量，它的值与零电势点的选取有关，由静电势能可计算电荷或电荷系统（如电偶极子）所受的力和力矩。

静电位能造价信息

市场价
信息价
询价

防静电砂浆

规格型号：
25kg规格包装;16kg/平方/公分;1.6吨/立方
价格行情：
材料单位：
吨
材料品牌：
金砼宝
材料税率：
13%
供应商：
广州市砼宝科技有限公司
报价时间：
2022-12-07

查看价格

PVC同质透心防静电地板

规格型号：
PVC同质透心防静电地板 2.0mm×2m×20m; Gemmaflor洁玛E格
价格行情：
材料单位：
m²
材料品牌：
Gemmaflor洁玛
材料税率：
13%
供应商：
洁玛新材料股份有限公司
报价时间：
2022-12-07

查看价格

防静电环氧底漆A组分

规格型号：
FL1120A
价格行情：
材料单位：
kg
材料品牌：
嘉宝莉
材料税率：
13%
供应商：
广州嘉宝莉地坪材料有限公司
报价时间：
2022-12-07

查看价格

导静电环氧底漆A组分

规格型号：
FL1122A
价格行情：
材料单位：
kg
材料品牌：
嘉宝莉
材料税率：
13%
供应商：
广州嘉宝莉地坪材料有限公司
报价时间：
2022-12-07

查看价格

水性环氧导静电底漆B组分

规格型号：
FL1362B
价格行情：
材料单位：
kg
材料品牌：
嘉宝莉
材料税率：
13%
供应商：
广州嘉宝莉地坪材料有限公司
报价时间：
2022-12-07

查看价格

电

规格型号：
机械用
价格行情：
材料单位：
kW·h
材料税率：
地区时间：
阳江市2022年10月信息价
所属行业：
建筑工程
备注说明：

查看价格

电

规格型号：
机械用
价格行情：
材料单位：
kW·h
材料税率：
地区时间：
阳江市2022年9月信息价
所属行业：
建筑工程
备注说明：

查看价格

电

规格型号：
机械用
价格行情：
材料单位：
kW.h
材料税率：
地区时间：
阳江市阳西县2022年9月信息价
所属行业：
建筑工程
备注说明：

查看价格

电

规格型号：
机械用
价格行情：
材料单位：
kW.h
材料税率：
地区时间：
阳江市海陵岛区2022年9月信息价
所属行业：
建筑工程
备注说明：

查看价格

电

规格型号：
机械用
价格行情：
材料单位：
kW·h
材料税率：
地区时间：
潮州市饶平县2022年8月信息价
所属行业：
建筑工程
备注说明：

查看价格

防静电接地等电位盒

规格型号：
-
需求量：
1台
报价数：
1
材料品牌：
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2021-12-24

查看价格

防静电涂层

规格型号：
1.防静电涂层
需求量：
893.0497m²
报价数：
3
材料品牌：
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2021-08-26

查看价格

数据统计公式配置

规格型号：
配置计算量统计公式,分单个泵房和高中低区泵房(泵房的综合配水和供水单耗单耗,水泵的综合和配水单耗,消毒供水单耗,总用电量,水泵,消毒,照明,空调,除湿机,插座的用电量,供水量和平均压力)的小时数据和天数据总共48个相关公司配置和数据检查核对等.每个泵房按照中级软件工程师0.6人天计算.
需求量：
99套
报价数：
3
材料品牌：
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2022-03-27

查看价格

防静电地毯

规格型号：
防静电地毯
需求量：
1m²
报价数：
1
材料品牌：
材料档次：
费用说明：
含税费 | 不含运费
询价时间：
2009-05-15

查看价格

防静电漆

规格型号：
防静电漆
需求量：
100kg
报价数：
1
材料品牌：
材料档次：
费用说明：
含税费 | 含运费
询价时间：
2011-11-15

查看价格

静电位能简介

由于静电场是保守场，也即在静电场中移动电荷时，静电场力作功与路径无关，所以任一电荷在静电场中都具有势能，这势能叫静电位能（或静电势能）。 在力学中，重力是保力势能的概念；弹性力是保守力，可以引入弹性势能；由于静电场也是保守场，所以在研究静电力做功时，也可以引入相应的静电势能（简称电势能）的概念。

静电位能单位

国际单位制中，电势能的单位就是一般能量的单位，即焦耳，符号为 。 还有一种常用的能量单位名称为电子伏，符号为 ，1 表示1个电子通过1 电势差时所获得的动能， 。

静电位能计算公式常见问题

等电位能跟地线连接吗

等电位是专用的，是不能和地线连接的，比如家里的电热水器，还有其他的一些卫生间的电器应该连接到等电位箱里，等电位并不是和地线端子一样的。家里用的等电位箱有两种区别，一个是局部等电位箱，一个是辅助等电位箱...
利用两点不同的地电位能否点亮灯泡？

1 首先明白为什么有电位差，这个电位差接地电阻不一样引起的，假如公用一个接地点的话这个电位差是由于接头处电阻或线路电阻引起的电位差，这个电位差是很小的，真要大的话那要这个地还有什么用，那不挺危险的吗...
电缆吨数计算公式

不同规格型号电缆有不同重量，应该没有相应的计算公式想要相应的重量还是需要向电缆厂家索取

静电位能计算公式文献

电缆装箱计算公式

电缆装箱计算公式

电缆装箱计算公式

格式：pdf

大小：163KB

页数： 2页

电缆装箱计算公式轴高 ÷ 2= 轴宽如： 2 米÷2 = 1米宽轴高 ÷4 = 轴梆高 2 米÷ 4=0.5米轴梆轴宽÷ 线径 = 一层圈数轴梆高 ÷ 线径 =层数算轴公式： 2.6 米轴配 1.35 米宽考虑电缆最大弯曲半径 (层数 -1) X(圈数 -1) x3.14 x(轴高 -轴梆高 ) = 米数如 (2 米 -0.5轴梆高 ) 比如 33KV 3x95mm 外径 91mm--- 2x1x2m 轴大概装 210 米公式一 :A×B×C=电缆轴可以缠绕电缆米数，本公式适用于高压成品及电缆外径大概在 40mm 及以上（ A= 轴心宽除以线缆外径尺寸再减一的到一层可以缠绕电缆的圈数 )(B=轴梆深度除以线缆外径尺寸再减一得到一轴可以缠绕电缆的层数 )（C=轴高减一边轴梆深度乘以 3.14 得到本轴上中下几层的平均以后的每圈电缆米数）公式二 :①×②×③=电缆

在线阅读立即下载

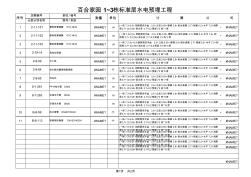水电计算公式

水电计算公式

水电计算公式

格式：pdf

大小：163KB

页数： 2页

定额编号部位 /轴号分部分项名称图号 /系统 1 2-11-151 塑料线管暗敷 PVCΦ20 #NAME? m [一栋 7.3+0.5+到厨房洗手盆 3.5+立起 0.55+楼梯 2.8+到水表箱 2.7+预留 0.2+水平 7.2+到厨房3.7+立0.55+到水表 2.7+0.2预留 )*3 栋 *1层 = #NAME? 2 2-11-152 塑料线管暗敷 PVCΦ25 #NAME? m {一栋 7.3+0.5+到厨房洗手盆 3.5+立起 0.55+楼梯 2.8+到水表箱 2.7+预留 0.2+水平 7.2+到厨房 3.7+立0.55+到水表 2.7+0.2预留 )*3 栋 *2层 = #NAME? 3 2-11-153 塑料线管暗敷 PVCΦ32 #NAME? m (一栋 7.3 ‰ +0.5+到厨房洗手盆 3.5+立起 0.55+楼梯 2.8+到水表箱 2.7+预

在线阅读立即下载

位能扰动位能理论及其应用和概念

针对局地环流能量转换问题，该工作系列讨论扰动位能理论及其应用。提出了扰动位能的新概念，将其分解为大气扰动位能(简称扰动位能)和表面扰动位能两个部分，给出了扰动位能各阶矩项的数学表达形式，结合资料指出二阶以上的扰动位能高阶矩项相对于其一阶矩项和二阶矩项来说是小量，并指出扰动位能二阶矩项的全球平均恰好等于传统的有效位能，但两者在物理意义上明显不同。 位能扰动位能的季节变化 扰动位能有明显的季节变化。从冬季和夏季带面积加权的整层大气扰动位能一阶矩项、二阶矩项及它们总和的垂直平均的全球分布。可知无论是扰动位能的一阶矩项、二阶矩项还是它们的总和都是冬半球的分布与年平均的情形相似。 与年平均情况一样，扰动位能的冬夏分布形势和变化与扰动位能一阶矩项的相似。从冬夏扰动位能的差可以较好地反映其年变化。在热带地区，由于太阳辐射变化不大而整层大气扰动位能的一阶矩项、二阶矩项以及扰动位能本身的年变化较小，这些量的年变化在陆地上比在海洋上要大。扰动位能的一阶矩项和扰动位能由冬到夏在北半球基本上是增大(除了北半球热带地区)，而在南半球则相反，增大和减弱最显著的地区分别位于大陆的上空。 南、北半球和全球平均的整层大气扰动位能的季节变化，可见半球平均的整层大气扰动位能的季节变化是显著的，但全球平均的季节变化很小，基本稳定。对于一阶矩项，北半球平均值夏季最大，冬季最小，南半球平均值正好相反，它们季节变化的幅度约为70×10⁶J。对于二阶矩项，南、北半球平均值的变化与一阶矩项的相反，其季节变化的幅度约为3.5×10⁶J，约是一阶矩项的二十分之一。为了维持平衡，存在着平均一阶矩项从冬半球向夏半球、平均二阶矩项从夏半球向冬半球的越赤道输送。 位能扰动位能与动能之间的联系 南、北半球和全球平均的整层大气总动能的季节变化与扰动位能二阶矩项的变化情况极为相似，似乎呈一固定的比例。这一点可以通过提供的南半球、北半球和全球平均的整层大气总动能和扰动位能二阶矩项的比值得到反映，对于全球平均而言，它们的比值较半球尺度情况更稳定，平均而言约为20%,说明从全球尺度上大气总动能的季节变化与扰动位能二阶矩项的关系密切。但从区域尺度或局地上看，两者之间的关系不明确，年平均整层大气总动能与扰动位能的二阶矩项之比的分布，可以看出一些急流区和季风区内的情况，同时，可见有些地区大气动能比扰动位能二阶矩项的数值还大不少，特别是在南北两半球副热带急流区，而且在这些地区在不同的季节大气动能比扰动位能二阶矩项甚至大80～100倍以上，表明在区域或局地的尺度，扰动位能二阶矩项并不能代表全位能中可以释放的那一部分(即全位能变为动能的部分)。然而，大气动能却与扰动位能一阶矩项的关系密切，两者呈现非常清楚的反向变化关系，其实对于任何局地上的情况都是如此，这种结果是符合能量学观点的，说明扰动位能对于局地环流动能维持的重要性。

最小位能原理弹性理论中的最小位能原理

弹性理论中的最小位能原理是用应变变分表示的弹性力学变分原理。 对于给定的弹性体，真实发生的位移使体系总位能的一次变分为零。记位移为u=(u₁,u₂,u₃)，应变为 应力为σ_ij，体积力密度为F=(F₁,F₂,F₃)，表面力密度为P=(P₁,P₂,P₃)，体系总位能为 以位移变分表示位能的变分，则有

位能位能与势场

势场又称保守力场这些力都称为保守力，保守力的特点是它对物体或电荷做功的大小，只和物体或电荷的始点和终点的位置有关，而和所循的途径无关。即当始、终点固定时，循直线或循很复杂的曲线，保守力所作的功相同；循任意曲线回旋一周，保守力作功为零，物体或电荷恢复原来的能量状态，因此机械能守恒，并因此可用势能的变化来描述保守力作功的大小。非保守力也称耗散力，如摩擦力和粘性力等，其作功大小不仅和起、终点有关，也和所循途径有关，循曲线回旋一周，不能恢复原来的能量状态，即机械能有所损失或有所增加，存在机械能和其他能量的转换。分析质点在势场中的运动时，经常用到势能、动能的转换，因此势能是动力学中的一个重要概念。重力势能是物体因为重力作用而拥有的能量,公式为EP=mg△h)

相关推荐

相关百科
相关知识
相关专栏

免费服务热线: 400-888-9639