选择特殊符号
选择搜索类型
请输入搜索
用二叉链表做为存储结构,先序遍历算法可描述为:
void InOrder(BinTree T)
{ //算法里①~⑥是为了说明执行过程加入的标号
① if(T) { // 如果二叉树非空
② printf("%c",T->data); // 访问结点 ③ InOrder(T->lchild); ④ InOrder(T->rchild); ⑤ }
⑥ } // InOrder
void createBiTree(BiTree *bt){
char ch;
ch = getchar();
if(ch == '.')
*bt = NULL;
else{
*bt = (BiTree)malloc(sizeof(BiTNode));//向内存申请节点空间
(*bt)->data = ch;
createBiTree(&((*bt)->LChild));//生成左子树
createBiTree(&((*bt)->RChild));//生成右子树
}
}/*createBiTree*/
/*==================打印二叉树=============*/
void printTree(BiTree bt,int nLayer){
int i;
if(bt == NULL)
return ;
printTree(bt ->RChild,nLayer+1);
for(i=0;i<nLayer;i++)
printf(" ");
printf("%c\n",bt->data);
printTree(bt->LChild,nLayer+1);
}
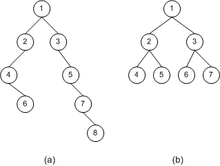
图一:
(a)1 2 4 . . 6 . . 3 . 5 . 7 . 8 . .
(b)1 2 4 . . 5 . . 3 6 . . 7 . . 运行结果:
图二:
(a)7 3 1 . . 2 . . 9 . 10 . 8 . 4 . .
(b)7 3 1 . . 5 4 . . . 11 10 . . 15 . .
运行结果:

在使用扩展先序遍历创建二叉树时,首先要根据一棵二叉树写出它的先序遍历序列,然后根据图中各个节点左右孩子的 状况进行加点遍历,凡是没有左右孩子的节点,遍历到它的左右孩子是都用"."表示它的左右孩子,注意这里面的"."只是用来表示它的父节点没有它这个左孩子或右孩子,并不表示节点,所以在遍历过程中应该访问到"."就结束了,不能再沿着"."继续遍历。
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问 题。 遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础。本节主要讲二叉树中遍历过程,遍历方法,重点介绍扩展先序遍历序列以及利用此序列创建二叉树的过程,顺便比较一下各种遍历方法的异同和应用。
从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此,在任一给定结点上,可以按某种次序执行三个操作:
(1)访问结点本身(N),
(2)遍历该结点的左子树(L),
(3)遍历该结点的右子树(R)。
根据遍历的原则:先左后右,对于先序遍历,顾名思义就是先访问根节点,再访问左子树,最后访问右子树,
从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此,在任一给定结点上,可以按某种次序执行三个操作:
(1)遍历该结点的左子树(L),
(2)访问结点本身(N),
(3)遍历该结点的右子树(R)。
对于中序遍历,就是先访问左子树,再访问根节点,最后访问右子树;
从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此,在任一给定结点上,可以按某种次序执行三个操作:
(1)遍历该结点的左子树(L),
(2)遍历该结点的右子树(R)。
(3)访问结点本身(N),
对于后序遍历,就是先访问左子树,再访问右子树,最后访问根节点;
根据访问结点操作发生位置命名:
① NLR:前序遍历(PreorderTraversal亦称(先序遍历))
--访问根结点的操作发生在遍历其左右子树之前。
② LNR:中序遍历(InorderTraversal)
--访问根结点的操作发生在遍历其左右子树之中(间)。
③ LRN:后序遍历(PostorderTraversal)
--访问根结点的操作发生在遍历其左右子树之后。
第一步:菱形斜填写 第二步:菱形四角的3和7,1和9交换,如下图 第三步:9和1插队进去,如图先将1—9九个数按如下图排列14 b 27 c 5 a 38 d 69然后将a用7代替,同理1换d,3...
短跑的就是计算150厚度,按其水平投影面积计算,包含一半的梯井调出的板应该是单独计算,计入在挑檐板中吧
一般都是300宽 3MM厚,这样每米重量为0.3*3*7.85=7.065kg,这样一吨为1000/7.065=141m

 等效焓降扩展算法的比较和联合应用
等效焓降扩展算法的比较和联合应用
等效焓降扩展算法的比较和联合应用
等效焓降扩展算法的比较和联合应用——等效焓降法用于分析热力系统、计算热经济性指标时,十分简便、迅速,而且运算结果准确,所以应用也很广泛。面对热力系统中不同的问题和要求,我国学者在等效焓降法的基础上,提出了很多不同的改进算法。与等效焓降法相比,它们在...

 南邮大数据结构上机实验四内排序算法地实现以及性能比较
南邮大数据结构上机实验四内排序算法地实现以及性能比较
南邮大数据结构上机实验四内排序算法地实现以及性能比较
实用标准 文案大全 实 验 报 告 ( 2015 / 2016 学年 第二学期) 课程名称 数据结构 A 实验名称 内排序算法的实现以及性能比较 实验时间 2016 年 5 月 26 日 指导单位 计算机科学与技术系 指导教师 骆健 学生姓名 耿宙 班级学号 B14111615 学院 (系) 管理学院 专 业 信息管理与信息系统 实用标准 文案大全 实习题名 :内排序算法的实现及性能比较 班级 B141116 姓名 耿宙 学号 B14111615 日期 2016.05.26 一、 问题描述 验证教材的各种内排序算法, 分析各种排序算法的时间复杂度; 改进教材中的快速 排序算法,使得当子集合小于 10个元素师改用直接插入排序;使用随即数发生器产生 大数据集合, 运行上述各排序算法, 使用系统时钟测量各算法所需的实际时间, 并进行 比较。系统时钟包含在头文件“ time.h
树中节点结构为:
核心代码:
· Preorder前序遍历--访问结点的操作发生在遍历其左右子树之前
· Inorder中序遍历--访问结点的操作发生在遍历其左右子树之间
· Postorder后序遍历--访问结点的操作发生在遍历其左右子树之后
· Level order层次遍历--按每一层的节点,从左到右逐次访问
树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的系统的访问,即依次对树中每个结点访问一次且仅访问一次。树的3种最重要的遍历方式分别称为前序遍历、中序遍历和后序遍历。以这3种方式遍历一棵树时,若按访问结点的先后次序将结点排列起来,就可分别得到树中所有结点的前序列表,中序列表和后序列表。相应的结点次序分别称为结点的前序、中序和后序。
树的这3种遍历方式可递归地定义如下:
§ 如果T是一棵空树,那么对T进行前序遍历、中序遍历和后序遍历都是空操作,得到的列表为空表。
§ 如果T是一棵单结点树,那么对T进行前序遍历、中序遍历和后序遍历都只访问这个结点。这个结点本身就是要得到的相应列表。
§ 否则,设T如图6所示,它以n为树根,树根的子树从左到右依次为T1,T2,..,Tk,那么有:
§ 对T进行前序遍历是先访问树根n,然后依次前序遍历T1,T2,..,Tk。
§ 对T进行中序遍历是先中序遍历T1,然后访问树根n,接着依次对T2,T2,..,Tk进行中序遍历。
§ 对T进行后序遍历是先依次对T1,T2,..,Tk进行后序遍历,最后访问树根n。