中序遍历
中序遍历(LDR)是二叉树遍历的一种,也叫做中根遍历、中序周游。在二叉树中,先左后根再右。巧记:左根右。
-

选择特殊符号
选择搜索类型
请输入搜索
中序遍历(LDR)是二叉树遍历的一种,也叫做中根遍历、中序周游。在二叉树中,先左后根再右。巧记:左根右。

树中节点结构为:
核心代码:
1、在软件中,新建梁构件时,在名称栏修改成图纸上对应的梁名称. 2、当定义了很多构件后,可以点"排序",选择按照名称\子类型\子类型和名称\创建顺序\尺寸排序(大到小)即可。
零序:1、零序一般指的是三相系统中的不平衡分量,零序电流由三相不平衡时感应或者产生。一般都是穿过电缆的三条主线。零序电压是开口三角形,平时无电压或者很小,故障状态产生。在继电保护装置中设置一定的数值,...
排序对造价是没有影响的,如果甲方给的格式中有说明按照一定的格式,他们会给你格式的,这样你就直接输入就可以了

 基于特征遍历技术的机械零件参数化设计
基于特征遍历技术的机械零件参数化设计
基于特征遍历技术的机械零件参数化设计
阐述了特征遍历的原理,提出一种基于特征遍历的参数化设计方法。以CAA为开发平台,VC++为编程工具,实现了此方法在CATIA环境下的运用。此方法基于特征遍历技术,在运用上具有普适性,可以有效提高设计效率。

 模板法制备沥青烯基有序结构中孔炭
模板法制备沥青烯基有序结构中孔炭
模板法制备沥青烯基有序结构中孔炭
以煤炭直接液化工艺过程的副产物——沥青烯为碳源,中孔硅分子筛SBA-15为模板,采用模板炭化法制备了具有规则结构的中孔炭。制备过程包括利用溶剂夹带法将沥青烯填充到模板孔道内,炭化模板孔道内的沥青烯以及脱除模板等步骤。利用扫描电镜、透射电镜、粉末X射线衍射仪对产品的微观形貌和结构进行了分析;测定了材料的抗氧化性能、导电性能以及对N2的吸附特性。结果表明:产品具有对模板结构反转复制的规则结构,其比表面积为562m2/g,孔容为0.566cm3/g,孔尺寸呈单分布,平均孔径为3.57nm;此外,材料具有良好的抗氧化性能,空气环境下300℃处理后样品仍保持规则的孔结构形态;其平均电阻率为0.16Ω.cm左右,属半导体材料导电性能范畴。
在使用扩展先序遍历创建二叉树时,首先要根据一棵二叉树写出它的先序遍历序列,然后根据图中各个节点左右孩子的 状况进行加点遍历,凡是没有左右孩子的节点,遍历到它的左右孩子是都用"."表示它的左右孩子,注意这里面的"."只是用来表示它的父节点没有它这个左孩子或右孩子,并不表示节点,所以在遍历过程中应该访问到"."就结束了,不能再沿着"."继续遍历。
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问 题。 遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础。本节主要讲二叉树中遍历过程,遍历方法,重点介绍扩展先序遍历序列以及利用此序列创建二叉树的过程,顺便比较一下各种遍历方法的异同和应用。
从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此,在任一给定结点上,可以按某种次序执行三个操作:
(1)访问结点本身(N),
(2)遍历该结点的左子树(L),
(3)遍历该结点的右子树(R)。
根据遍历的原则:先左后右,对于先序遍历,顾名思义就是先访问根节点,再访问左子树,最后访问右子树,
从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此,在任一给定结点上,可以按某种次序执行三个操作:
(1)遍历该结点的左子树(L),
(2)访问结点本身(N),
(3)遍历该结点的右子树(R)。
对于中序遍历,就是先访问左子树,再访问根节点,最后访问右子树;
从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此,在任一给定结点上,可以按某种次序执行三个操作:
(1)遍历该结点的左子树(L),
(2)遍历该结点的右子树(R)。
(3)访问结点本身(N),
对于后序遍历,就是先访问左子树,再访问右子树,最后访问根节点;
根据访问结点操作发生位置命名:
① NLR:前序遍历(PreorderTraversal亦称(先序遍历))
--访问根结点的操作发生在遍历其左右子树之前。
② LNR:中序遍历(InorderTraversal)
--访问根结点的操作发生在遍历其左右子树之中(间)。
③ LRN:后序遍历(PostorderTraversal)
--访问根结点的操作发生在遍历其左右子树之后。
用二叉链表做为存储结构,先序遍历算法可描述为:
void InOrder(BinTree T)
{ //算法里①~⑥是为了说明执行过程加入的标号
① if(T) { // 如果二叉树非空
② printf("%c",T->data); // 访问结点 ③ InOrder(T->lchild); ④ InOrder(T->rchild); ⑤ }
⑥ } // InOrder
void createBiTree(BiTree *bt){
char ch;
ch = getchar();
if(ch == '.')
*bt = NULL;
else{
*bt = (BiTree)malloc(sizeof(BiTNode));//向内存申请节点空间
(*bt)->data = ch;
createBiTree(&((*bt)->LChild));//生成左子树
createBiTree(&((*bt)->RChild));//生成右子树
}
}/*createBiTree*/
/*==================打印二叉树=============*/
void printTree(BiTree bt,int nLayer){
int i;
if(bt == NULL)
return ;
printTree(bt ->RChild,nLayer+1);
for(i=0;i<nLayer;i++)
printf(" ");
printf("%c\n",bt->data);
printTree(bt->LChild,nLayer+1);
}
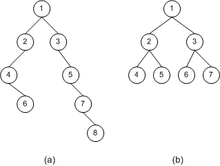
图一:
(a)1 2 4 . . 6 . . 3 . 5 . 7 . 8 . .
(b)1 2 4 . . 5 . . 3 6 . . 7 . . 运行结果:
图二:
(a)7 3 1 . . 2 . . 9 . 10 . 8 . 4 . .
(b)7 3 1 . . 5 4 . . . 11 10 . . 15 . .
运行结果:
树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的系统的访问,即依次对树中每个结点访问一次且仅访问一次。树的3种最重要的遍历方式分别称为前序遍历、中序遍历和后序遍历。以这3种方式遍历一棵树时,若按访问结点的先后次序将结点排列起来,就可分别得到树中所有结点的前序列表,中序列表和后序列表。相应的结点次序分别称为结点的前序、中序和后序。
树的这3种遍历方式可递归地定义如下:
§ 如果T是一棵空树,那么对T进行前序遍历、中序遍历和后序遍历都是空操作,得到的列表为空表。
§ 如果T是一棵单结点树,那么对T进行前序遍历、中序遍历和后序遍历都只访问这个结点。这个结点本身就是要得到的相应列表。
§ 否则,设T如图6所示,它以n为树根,树根的子树从左到右依次为T1,T2,..,Tk,那么有:
§ 对T进行前序遍历是先访问树根n,然后依次前序遍历T1,T2,..,Tk。
§ 对T进行中序遍历是先中序遍历T1,然后访问树根n,接着依次对T2,T2,..,Tk进行中序遍历。
§ 对T进行后序遍历是先依次对T1,T2,..,Tk进行后序遍历,最后访问树根n。