选择特殊符号

Ф δ ° × # Ⅱ Ⅲ ½ ¼

选择搜索类型

市场价信息价参考价询价供应商云知资讯文库百科

热门搜索

造价通

请输入搜索

首页 > 百科 > 建设工程百科

转轴倾角

转轴倾角，是指行星的自转轴相对于轨道平面的倾斜角度，也称为(obliguity)或轴交角(axial inclination)。 在天文学上，是以自转轴与穿过行星的中心点并垂直于轨道平面的直线之间所夹的角度来表示与度量。转轴倾角也可以等效的表示为行星的轨道平面和垂直于自转轴的平面所夹的角度。

转轴倾角基本信息

中文名转轴倾角
外文名axial inclination
别名倾角
简介行星自转轴相对于轨道平面的角度

转轴倾角数值

地球自转轴的倾斜在22.1° 至 24.5° 之间变化者，周期是41,000年，而目前正在减少中。除了稳定的减少之外，还有一个较短的18.6年周期，也就是所谓的章动。 太阳系数值模形 依据西蒙·纽康的计算，地球在19世纪末的转轴倾角是23° 27’ 8.26” (1900年的历元)，而在望远镜能更精确的测量之前，这也是一般所接受的数值。电子计算机可以进行使更加精确的模型计算，在1976年，Lieske使用改良的模型得到黄赤交角的值ε = 23° 26’ 21.448” (2000年的历元)。这一部分在2000年已经成为国际天文联合会推荐的简要计算式中的一部分： ε = 84,381.448 − 46.84024T − (59 × 10)T² (1,813 × 10)T³，以秒为价算的单位，T是从星历表2000.0历元 (相当于儒略日 2,451,545.0) 起算的儒略世纪 (36,525日)。这个算式也适用纽康的计算数值，以线性的部分可以回推至1900年 (T = -1)。 观察T的线性部分是负值，所以现在的黄赤交角正在慢慢的减小。这个公式也暗示仅仅是在合理的T范围内给了ε一个近似值。如果不是这样，当T趋近于无限时，ε也会趋近无限。根据太阳系数值模形，显示ε有着41,000年的循环周期，与分点岁差一样有个常数值 (虽然不是岁差本身)。 其它的理论模型 其它的理论模型也许可以用更高阶的T展开来表演算ε的数值，但是因为没有多项式 (有限的) 可以表现出周期性，当T'增加至足够大时，不是趋向正的无限大，就是负的无限大。因此您应该可以了解国际天文联合会为何决定选择与多数数学模型一致的一次方程式。在5,000年尺度内的过去和未来，可以满足所有的模型，在9,000年尺度内的过去和未来，大部分仍有合理的准确性。而对更长远的时代，彼此间的矛盾就太大了。

转轴倾角造价信息

市场价
信息价
询价

转轴联锁

规格型号：
品种:断路器附件;系列:CVR2-12;规格:分闸联锁+合闸联锁;
价格行情：
材料单位：
套
材料品牌：
常熟开关
材料税率：
13%
供应商：
上海西屋开关有限公司
报价时间：
2022-12-06

查看价格

大倾角输送带

规格型号：
1000×5带宽(mm):1000;输送带类型:环形输送带20-49米;材质:尼龙;
价格行情：
材料单位：
m²
材料品牌：
盛阳
材料税率：
13%
供应商：
保定华阳橡胶机带有限公司驻沈阳办事处
报价时间：
2022-12-06

查看价格

转轴联锁

规格型号：
品种:断路器附件;系列:CVR2-12;规格:分闸连锁;
价格行情：
材料单位：
套
材料品牌：
常熟开关
材料税率：
13%
供应商：
上海西屋开关有限公司
报价时间：
2022-12-06

查看价格

转轴联锁

规格型号：
品种:断路器附件;系列:CVR1-12;规格:分闸连锁;
价格行情：
材料单位：
套
材料品牌：
常熟开关
材料税率：
13%
供应商：
上海西屋开关有限公司
报价时间：
2022-12-06

查看价格

转轴联锁

规格型号：
品种:断路器附件;系列:CVR1-12;规格:分闸联锁+合闸联锁;
价格行情：
材料单位：
套
材料品牌：
常熟开关
材料税率：
13%
供应商：
上海西屋开关有限公司
报价时间：
2022-12-06

查看价格

单卧轴式混凝土搅拌机

规格型号：
出料容量150L
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2012年4季度信息价
所属行业：
建筑工程
备注说明：

查看价格

单卧轴式混凝土搅拌机

规格型号：
出料容量250L
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2012年4季度信息价
所属行业：
建筑工程
备注说明：

查看价格

双卧轴式混凝土搅拌机

规格型号：
出料容量1500L
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2012年4季度信息价
所属行业：
建筑工程
备注说明：

查看价格

单卧轴式混凝土搅拌机

规格型号：
出料容量250L
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2012年3季度信息价
所属行业：
建筑工程
备注说明：

查看价格

单卧轴式混凝土搅拌机

规格型号：
出料容量350L
价格行情：
材料单位：
台班
材料税率：
地区时间：
汕头市2012年3季度信息价
所属行业：
建筑工程
备注说明：

查看价格

转轴

规格型号：
消防门转轴
需求量：
2.0根
报价数：
3
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2014-05-08

查看价格

转轴

规格型号：
直径50×100
需求量：
8个
报价数：
1
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2011-12-08

查看价格

转轴

规格型号：
100mm
需求量：
1套
报价数：
2
材料品牌：
无
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2015-06-08

查看价格

转轴

规格型号：
管井暗门
需求量：
9.0m
报价数：
3
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2015-03-17

查看价格

转轴

规格型号：
-
需求量：
10.8m
报价数：
3
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2014-05-28

查看价格

转轴倾角长周期变化

然而以外插法展开的平均多项式可以得到一条正弦曲线符合41,013年的周期，依据Wittmann,的公式，相当于： ε = AB sin (C(TD))，此处 A = 23.496932° ± 0.001200°，B = − 0.860° ± 0.005°，C = 0.01532 ± 0.0009 径/儒略世纪， D = 4.40 ± 0.10儒略世纪，还有T'是以2000.0历元为起点的世纪数。 黄赤交角的平均范围从22° 38’ 至 24° 21’，过去的最大值出现在西元前8,700年，均值是在1,500年，而未来的极小值将在11,800年。这个算式应该可以合理的推算过去以及未来数百万年的概略数值。然而这个算式在振幅上表持着相同的数值，但是从米兰科维奇循环的结果是有不规则的变化发生，其所引述的范围是从21° 30’ 至 24° 30’，仅是低值就超越正常的22° 30’达1°之多。如果我们往回追溯五百万年，黄道面的倾角 (或许更精确地说应该是赤道在黄道上的移动) 会在22.0425° 至24.5044°，但是在未来的一百万年，这个范围只会在22.2289° 至24.3472°之间。 其它行星的转轴倾角也会改变，例如火星的范围相信是在15° 和 35°之间。地球的变动相对较小是归因于月球稳定的影响，但并非永远都是如此。依据沃德的说法，由于潮汐作用，在未来的15亿年，地月的距离将从现在的60倍地球半径增加至66.5倍地球半径。这种情况一但发生，跟随而来的行星共振效应将导致摆动的范围在22° 至38°。在往后，大约20亿年时，月球的距离达到68倍的地球半径，其他的共振会造成更大幅度的震荡，范围从27°到60°，在气候上将会有极端的变化。

转轴倾角倾角

转轴倾角也可以等效的表示为行星的轨道平面和垂直于自转轴的平面所夹的角度。在太阳系，地球的轨道平面就是黄道，所以地球的转轴倾角特别称为黄赤交角，并以希腊字母的ε (Epsilon) 作为表示的符号。 地球的转轴倾角大约是23.44° (23° 26’)。虽然在一整年之中转轴倾角都朝着相同的方向，但是因为地球绕着太阳运行，因此原先朝向太阳的半球会逐渐改变成背离太阳的半球，反之亦然。这种作用是造成季节变化的主要原因，无论是那一个半球朝向太阳，那个半球每天的日照时间就会比较长，并且阳光在正午时间触及地面的角度越接近垂直的方向，该地区在单位面积内得到的能量也越多。 低倾斜度造成极区接受到的太阳辐射减少，使得当地的环境有利于冰河作用。就像岁差和离心率的变化一样，转轴倾角的改变也会对季节变化造成重大的影响，只是在大冰河期开始时，转轴倾角的周期对高纬度地区影响特别显著。倾角的变化是一个造成冰河期或间冰期起伏的一个重要因素。 黄赤交角不是一个固定的值，会随着时间而改变。这种变化是很缓慢的，称为章动，精确的测量需要建立在每日数值变化的基础上，而这是天文学家的工作。黄赤交角的变化和春分点的岁差是以相同的理论来计算，并且有相互的关连性。较小的ε意味着有较大的p (黄经岁差)，反之亦然。实际上这两种运动不仅是各自独立的，并且在相互垂直的方向上。

转轴倾角常见问题

如何旋转轴网?

选中轴网点右健选择旋转，在下方的工具条中的旋转处前面的方框处打对勾，在后面输入度数，再点基准点即可。
怎么旋转轴网

选中轴网图元后单击旋转按钮按照软件提示操作即可。
组合型旋转轴网

在轴网绘图界面，选择修改轴号，修改成你想要的轴号就可以了，如下图：点击修改轴号位置---选择轴线---右键-----在弹出的窗口选择不标注即可。

转轴倾角测量

从地球表面观察和测量黄赤交角(ε)是天文学上很重要的知识和技能。观察太阳在天球上随着季节变化的位置，可以快速的掌握他的数值。测量在一年之中白天最长和最短的这两天正午太阳的高度差，这个差值是黄赤交角的两倍，在西元前1,000年的中国天文学家就是这样确定黄赤交角的。 太阳一年当中在天球上最北和最南的赤纬就相等于转轴倾角的角度。在一年当中，地球的转轴朝向太阳的那一天也是白天最长的一天，太阳的赤经是 23° 26’。一位在赤道上的观测者，在全年的观测中，当三月 (春分) 看见太阳在正午越过头顶的正上方，然后会发现每天正午的太阳逐渐向北移动，直到6月 (夏至) 离开天顶的角度达到ε度，在9月 (秋分) 太阳又再回到头顶的正上方，然后在12月 (冬至)又距离天顶ε度。 又例如：在纬度50°的观测者 (无论南纬或北纬)，在一年当中白天最长的那一天测得太阳在正午的高度是63° 26’，但在白天最短的那一天正午测得的高度只有16° 34’，两者的差是2ε = 46° 52’，所以ε = 23° 26’。 从算式可以得到距离地平的高度角： (90° - 50°) 23.4394° = 63.4394° (90° - 50°) - 23.4394° = 16.5606° 在赤道上，算式将被写成 90° 23.4394° = 113.4394° 和90° - 23.4394° = 66.5606° (永远从正南方的地平线计算高度。).

转轴倾角主要天体

主要天体的转轴倾角 天体 转轴倾角 (°) 水星 ~0.01 金星 177.36 地球 23.439 281 月球 1.5424 火星 25.19 谷神星 (矮行星) ~4 智神星 ~60 木星 3.13 土星 26.73 天王星 97.77 海王星 28.32 冥王星（矮行星） 119.61 阋神星 (矮行星) 不详（轨道倾角44.040 度）

转轴倾角文献

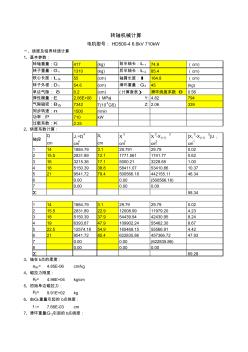转轴机械计算

转轴机械计算

转轴机械计算

格式：pdf

大小：32KB

页数： 2页

417 (kg) 前半轴长：L1 74.9 （cm）转子重量：G 1 1310 (kg) 后半轴长：L2 85.4 （cm）铁心长度：L fe 55 (cm) 轴肩长度：l 164.8 （cm）转子外径：D 1 54.6 (cm) 滑环重量：G2 45 (kg) 单边气隙： δ 0.2 (cm) (计算查表) 滑环绕度系数 θ 0.56 弹性模量：E 2.06E+06 （MPa） Y: 4.82 794 气隙磁密：Bδ 7342 T(10 4GS) Z: 2.06 339 1500 r/min 710 kW 2.25 Di Ji =Di 4 Xi Xi 3 Xi 3-X (i-1) 3 [X i 3-X(i-1) 3]/J i cm cm4 cm cm3 cm3 cm-1 1 14 1884.79 3.1 29.791 29.79 0.02 2 15.5 2831.89 12.1 1

在线阅读立即下载

转轴扭振测量基本原理.

转轴扭振测量基本原理.

转轴扭振测量基本原理.

格式：pdf

大小：32KB

页数： 3页

转轴扭振测量基本原理 1/3 转轴扭振测量基本原理 1 转轴扭振测试基本原理 [1] 图 1 转轴发生扭振时的角速度变化图 [1] 轴系扭振是在轴系的旋转过程中同时发生的运动现象。轴系正常稳定运行无扭振时，其按某一角速度 0ω回转。当轴系出现扭振时，会在轴截面上相应产生往复扭转变形值弧长 ' ''B B 或扭角 ? ，此时轴系的回转角速度因扭振引起的交变角速度 ωΔ 而发生了变化，其瞬时角速度为 0ω ω+Δ ，如图 1所示。按扭振信号的拾取方式分，扭振测量方法主要有两大类，即接触测量法和非接触测量法。接触测量法是将传感器 (应变片等 )安装在轴上，测量信号经过集流环或者无线电方式传给二次仪表。非接触测量一般采用“测齿法” ，即利用轴上的齿轮或其他等分结构，由磁电式、涡流式或光电式非接触传感器感受扭振引起的不均匀脉冲信号，通过二次仪表的解调处理后达到测量扭振的目的。图 2 角

在线阅读立即下载

转轴转轴图示

转轴主要用于机械工业方面的结构上，比如图1-图4所示。

转轴分类

按用途可分为以下9种类型：1、LCD转轴2、TV转轴3、可视电话转轴4、PDVD转轴5、DV 转轴6、数码相机转轴7、笔记本转轴8、手机转轴9、LED台灯转轴 按结构可分为以下9种类型：1、传统垫片转轴2、一字型转轴3、压铸工艺的转轴4、卷包转轴5、扭簧转轴 按功能可分为以下9种类型：1、无角度限制转轴2、有角度限制转轴3、多段扭力转轴4、定点转轴5、阻力转轴6、组合转轴7、挂壁转轴8、开关转轴

视倾角名称

视倾角读音 shì qīng jiǎo 视倾角别称 视倾角（apparent dip）又称假倾角。

相关推荐

相关百科
相关知识
相关专栏

免费服务热线: 400-888-9639