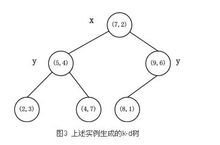
k-d树是一个二叉树,每个节点表示一个空间范围。表1给出的是k-d树每个节点中主要包含的数据结构。
表1 k-d树中每个节点的数据类型
域名 | 数据类型 | 描述 |
Node-data | 数据矢量 | 数据集中某个数据点,是n维矢量(这里也就是k维) |
Range | 空间矢量 | 该节点所代表的空间范围 |
split | 整数 | 垂直于分割超平面的方向轴序号 |
Left | k-d树 | 由位于该节点分割超平面左子空间内所有数据点所构成的k-d树 |
Right | k-d树 | 由位于该节点分割超平面右子空间内所有数据点所构成的k-d树 |
parent | k-d树 | 父节点 |
从上面对k-d树节点的数据类型的描述可以看出构建k-d树是一个逐级展开的递归过程。表2给出的是构建k-d树的伪码。
表2 构建k-d树的伪码
算法:构建k-d树(createKDTree) |
输入:数据点集Data-set和其所在的空间Range |
输出:Kd,类型为k-d tree |
1.If Data-set为空,则返回空的k-d tree |
2.调用节点生成程序: (1)确定split域:对于所有描述子数据(特征矢量),统计它们在每个维上的数据方差。以SURF特征为例,描述子为64维,可计算64个方差。挑选出最大值,对应的维就是split域的值。数据方差大表明沿该坐标轴方向上的数据分散得比较开,在这个方向上进行数据分割有较好的分辨率; (2)确定Node-data域:数据点集Data-set按其第split域的值排序。位于正中间的那个数据点被选为Node-data。此时新的Data-set' = Data-set\Node-data(除去其中Node-data这一点)。 |
3.dataleft = {d属于Data-set' && d[split] ≤ Node-data[split]} Left_Range = {Range && dataleft} dataright = {d属于Data-set' && d[split] > Node-data[split]} Right_Range = {Range && dataright} |
4.left = 由(dataleft,Left_Range)建立的k-d tree,即递归调用createKDTree(dataleft,Left_ Range)。并设置left的parent域为Kd; right = 由(dataright,Right_Range)建立的k-d tree,即调用createKDTree(dataright,Right_ Range)。并设置right的parent域为Kd。 |
以上述举的实例来看,过程如下:
由于此例简单,数据维度只有2维,所以可以简单地给x,y两个方向轴编号为0,1,也即split={0,1}。
(1)确定split域的首先该取的值。分别计算x,y方向上数据的方差得知x方向上的方差最大,所以split域值首先取0,也就是x轴方向;
(2)确定Node-data的域值。根据x轴方向的值2,5,9,4,8,7排序选出中值为7,所以Node-data = (7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于split = 0(x轴)的直线x = 7;
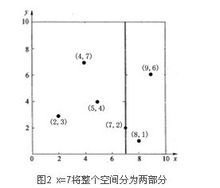
(3)确定左子空间和右子空间。分割超平面x = 7将整个空间分为两部分,如图2所示。x < = 7的部分为左子空间,包含3个节点{(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点{(9,6),(8,1)}。
如算法所述,k-d树的构建是一个递归的过程。然后对左子空间和右子空间内的数据重复根节点的过程就可以得到下一级子节点(5,4)和(9,6)(也就是左右子空间的'根'节点),同时将空间和数据集进一步细分。如此反复直到空间中只包含一个数据点,如图1所示。最后生成的k-d树如图3所示。