
作者:Mark Looney
摘要
MEMS陀螺仪提供了一种简单的旋转角速率测量方法,其所在的封装很容易安装到印刷电路板上。因此,在许多不同类型的运动控制系统中,它们都是反馈检测元件的常见选择。在此类应用中,角速率信号(MEMS陀螺仪输出)中的噪声会直接影响系统的关键特性(如平台稳定性),且常常是控制系统能够支持的精度水平的决定性因素。所以,当系统架构师和开发者定义和开发新的运动控制系统时,低噪声是一个很自然的价值导向。更进一步,把关键的系统级标准(如指向精度)转化为噪声指标(MEMS陀螺仪数据手册常常会提 供这些指标),是早期概念和架构设计工作的一个极重要的部分。了解系统对陀螺仪噪声特性的依赖性会产生多方面好 处,例如能够确定反馈检测元件的相关要求,或者相反,分析系统对特定陀螺仪中噪声的响应。一旦系统设计者充分了 解这种关系,它们便能从两个重要方面来掌控角速率反馈环路中的噪声影响:1. 制定最合适的MEMS陀螺仪选择标准;2. 在传感器的集成过程中保持其噪声性能不变。
运动控制基础
为了弄清MEMS陀螺仪噪声特性与其对系统关键特性的影响之间的关系,第一步常常是要对系统工作原理有一个基本了解。图1是一个运动控制系统架构示例,其中关键的系统元素被拆分为多个功能模块。此类系统的功能目标是为对惯性运动敏感的人员或设备创建一个稳定的平台。应用实例之一是用于自主驾驶车辆平台上的微波天线,车辆在恶劣的条件下机动行驶,车速可能会引起车辆方向突然变化。若不能实时控制指向角度,当发生此类惯性运动时,这些高指向性天线可能无法支持连续通信。

图1. 运动控制系统架构示例。
反馈环路图1. 运动控制系统架构示例。从MEMS陀螺仪开始,其在稳定平台上观测旋转速率 (φG)。陀螺仪的角速率信号馈入专用数字信号处理部分,其包括滤波、校准、对齐和积分,以产生实时方向反馈 (φE)。伺服电机的控制信号 (φCOR) 来自此反馈信号与指示方向 (φCMD) 的比较,而指示方向可来自一个中央任务处理系统,或者代表一个支持平台上的设备以理想方式运行的方向。
应用示例
图1显示了运动控制系统的架构视图,分析应用特定的物理性质也能得出有价值的定义和见解。考虑图2中的系统,它是生产线自动检查系统的概念视图。该摄像头系统检查输送带上移入移出其视场的物件。在这种配置中,摄像头通过一根长支架固定于天花板;针对摄像头要检查的对象大小,摄像头通过支架所决定的高度(参见图2中的D)来优化其视场。工厂中全是各种机器和其他作业,因此,摄像头会不时地发生 摆动(参见图2中的φSW(t)),这可能引起检查图像的失真。图中的红色虚线是此摆动引起的总角向误差 (±φSW) 的夸大视图,绿色虚线表示能够支持系统图像质量目标的角向误差水平 (±φRE)。图2中的视图利用检查表面上的线性位移误差(dSW、dRE)定义系统级关键指标(图像失真)。这些性质与摄像头高度 (D) 和角向误差项(ϕSW、φRE)之间有着简单的三 角函数关系,如公式1所示。

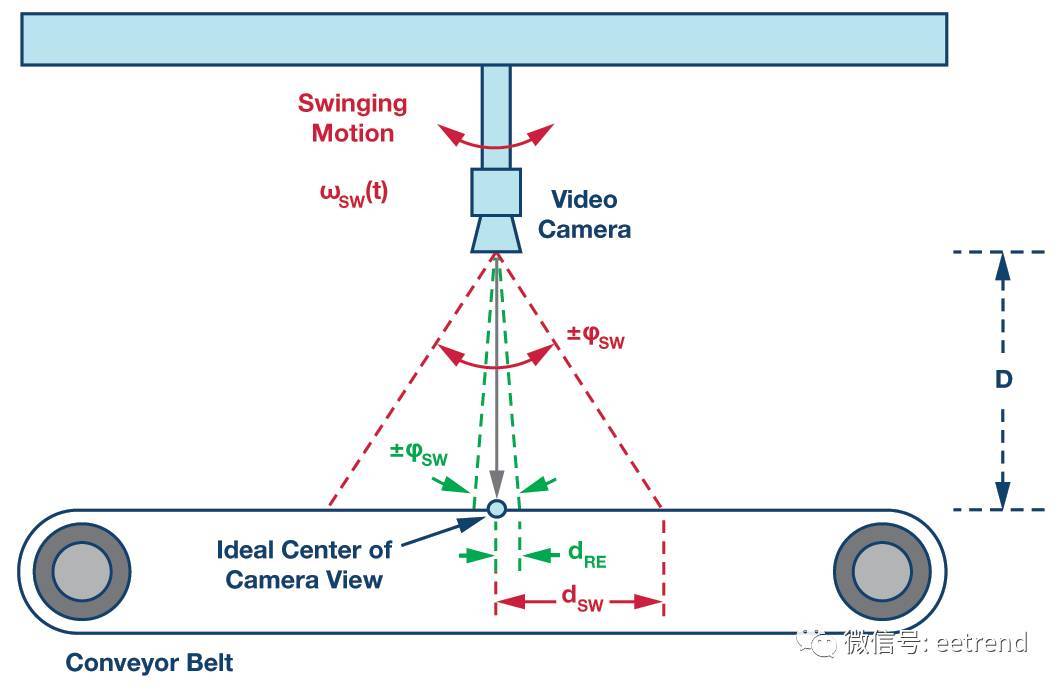
图2. 工业摄像头检查系统。
对于此类系统,最适合的运动控制技术是所谓图像稳定化技术。早期图像稳定系统使用基于陀螺仪的反馈系统来驱动伺服电机,进而调整图像传感器在快门开启期间的方向。MEMS技术的出现掀起了一场革命,帮助降低了这些功能的尺寸、成本和功耗,导致该技术广泛用于当今的数字摄像头。得益于数字图像处理技术(其算法中仍然使用基于MEMS的角速率测量)的进步,许多应用已不再使用伺服电 机。无论图像稳定是由伺服电机实现,还是通过对图像文件的数字后处理实现,陀螺仪的基本功能(反馈检测)依然未 变,其噪声影响也仍然存在。为简明起见,本讨论将聚焦于经典方法(图像传感器上的伺服电机)来考察相关度最高的 噪声基本原理,以及它们与此类应用最重要的物理性质之间的关系。
角向随机游动 (ARW)
所有MEMS陀螺仪的角速率测量中都有噪声。这一传感器固有噪声代表的是陀螺仪在静态惯性(无转动)和环境条件(无振动、冲击等)下运行时其输出中的随机振动。MEMS 陀螺仪数据手册中用来描述噪声特性的最常见指标是速率噪声密度 (RND) 和角向随机游动 (ARW) 。RND参数通常 以°/sec/ Hz为单位,根据该参数和陀螺仪的频率响应,可以简单地预测角速率方面的总噪声。ARW参数通常以°/ hr(小 时)为单位,当分析特定期间内噪声对角度估计的影响时,该参数常常更有用。公式2是根据角速率测量来估计角度的一 般公式。此外,它还提供了一个将RND参数与ARW参数关联起来的简单公式。此关系式与IEEE-STD-952-1997(附录C) 中的关系式相比有很小的改动(前者是单边FFT,后者是双边FFT)。

图3是一个图形参考,有助于我们进一步讨论ARW参数代表 的特性。图中的绿色虚线代表陀螺仪RND为0.004°/sec/ Hz时的ARW特性,相当于0.17°/ hr的ARW。实线代表此陀螺仪输出在25 ms周期内的六个独立积分。角向误差相对于时间的随机性表明,ARW的主要作用是估计特定积分时间内的角向误差统计分布。另请注意,此类响应假设利用高通滤波来消除积分过程中的偏置误差。
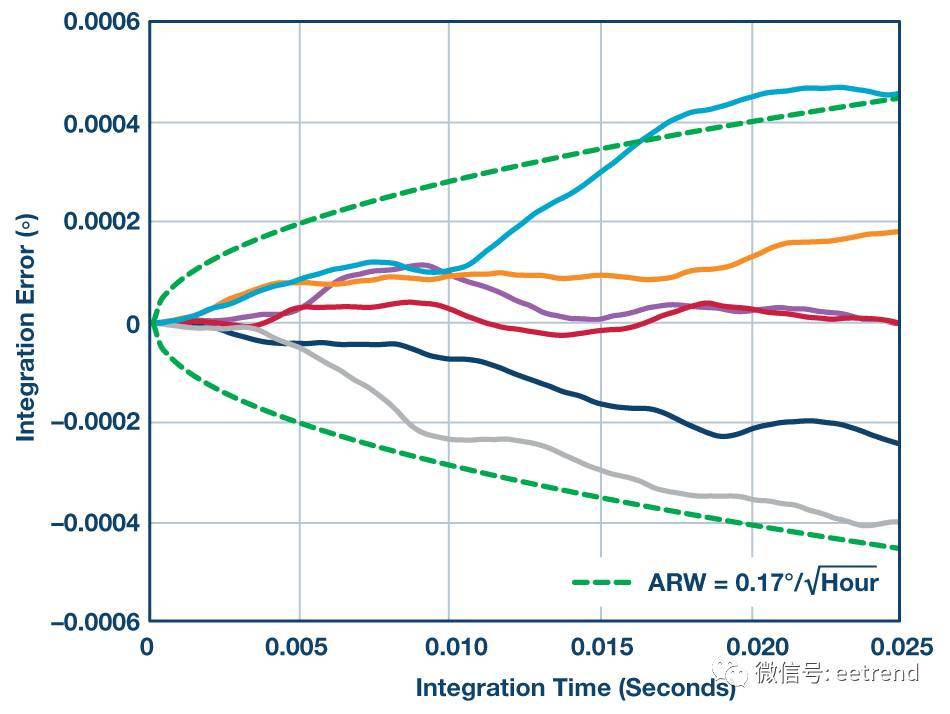
图3. 角向随机游动 (ADIS16460)。
回过头看图2中的应用示例,将公式1和公式2结合便可把重要标准(检查表面上的物理失真)与MEMS陀螺仪数据手册通常会提供的噪声性能指标(RND、ARW)关联起来。在此过程中,假设公式1中的积分时间 (τ) 等于图像捕捉时间可提供进一步且很有用的简化。公式3利用公式1中的一般关系来估 计,当摄像头距检查表面1米 (D) 且最大容许失真误差为10μm (dRE) 时,陀螺仪的角向误差 (φRE) 必须小于0.00057°。

公式4将公式3的结果和公式2中的一般关系相结合,用来预测特定情况下对MEMS陀螺仪的ARW和RND要求。该过程假设图像捕捉时间35 ms等于公式2中的积分时间 (τ),因而可以预 测,为了达到要求,陀螺仪的ARW需要小于0.18°/ hr,或者RND必须小于0.0043°/sec/ Hz。当然,这可能不是这些参数支持的唯一要求,但这些简单的关系提供了一个例子,告诉我们如何将其与已知要求和条件联系起来。

角速率噪声与带宽
提供连续指向控制的系统开发者可能更愿意从角速率方面来评估噪声影响,因为他们可能没有固定的积分时间来利用基于ARW的关系。从角速率方面评估噪声常常要考虑RND参数和陀螺仪信号链的频率响应。对陀螺仪频率响应影响最大的常常是滤波,其支持环路稳定标准的专用要求,并能抑制对 环境威胁(如振动)的不相干传感器响应。公式5给出了一种简单方法来估算与特定频率响应(噪声带宽)和RND相关的 噪声。
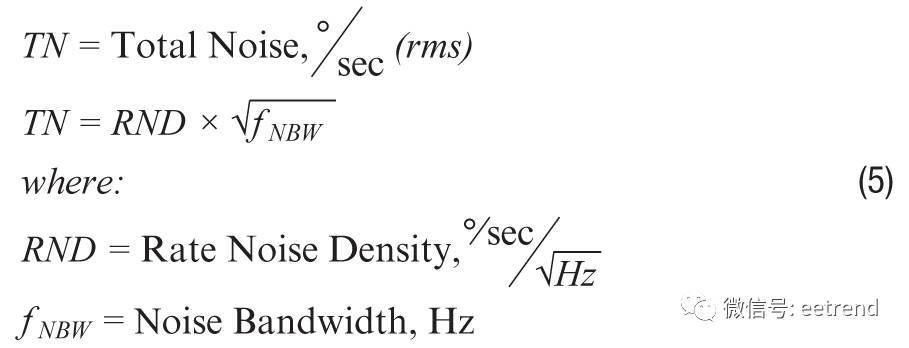
当RND的频率响应遵循单极点或双极点低通滤波器曲线时, 噪声带宽 (fNBW) 和滤波器截止频率 (fC) 将有公式6的关系。

例如,对于RND为0.004°/sec/ Hz的ADXRS290,图4提供了其噪声的两条不同频谱曲线。图中的黑色曲线代表使用双极点低通滤波器(截止频率为200 Hz)时的噪声响应,蓝色曲 线代表使用单极点低通滤波器(截止频率为20 Hz)时的噪声响应。公式7计算了各滤波器的总噪声。同预期一致,200 Hz 版本的噪声高于20 Hz版本。
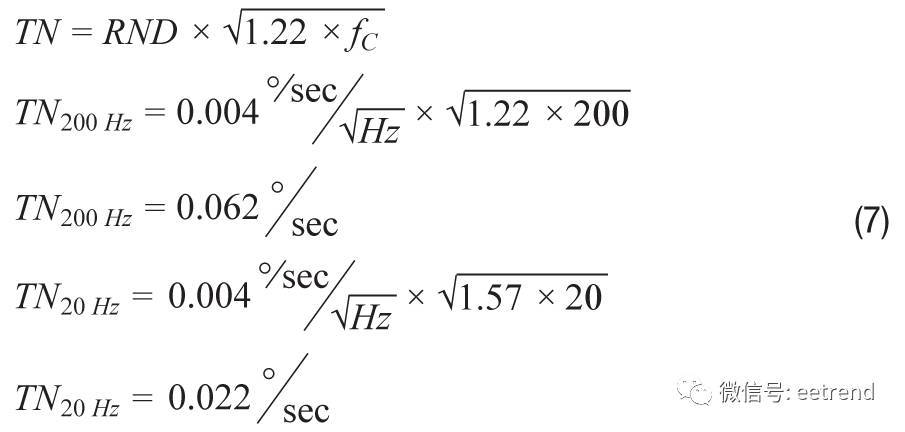

图4. 使用滤波器时的ADXRS290噪声密度。
若系统需要定制滤波,其频率响应 (HDF(f)) 不符合公式6和7中的简单单极点和双极点模型,则可利用公式8提供的更一般关系来预测总噪声:
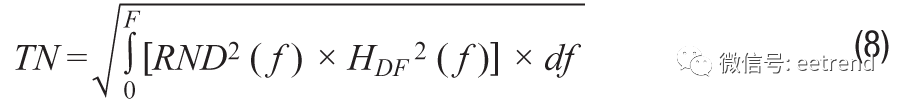
除了会影响总角速率噪声以外,陀螺仪滤波器还向总环路响应贡献相位延迟,这会直接影响反馈控制系统的另一重要品质因素:单位增益交越频率时的相位裕量。公式9用于估计单位增益交越频率 (fG) 时单极点滤波器(fC = 截止频率)对控制环路频率响应产生的相位延迟 (θ)。公式9中的两个例子分别是截止频率为200 Hz和60 Hz的两个滤波器在20 Hz单位增益交越频率时的相位延迟。这对相位裕量的影响可能导致要求陀螺仪带宽比单位增益交越频率大10倍,因而会更偏向于选择RND较佳的MEMS陀螺仪。

现代控制系统常常使用数字滤波器,可能使用不同的模型来预测其在控制环路关键频率时的相位延迟。例如,公式10用于预测一个16抽头FIR滤波器 (NTAP) 的相位延迟 (θ),其以 4250 SPS (fS) 的更新速率( ADXRS290 )运行,单位增益交越频率 (fG) 同样是20 Hz。此类关系有助于确定一个系统架构对此类滤波器结构容许的总抽头数。

结论
根本问题是角速率反馈环路中的噪声可能直接影响运动控制系统的关键性能标准,因此,在设计新系统的过程中,应当尽早予以考虑。相比于仅知道需要低噪声的人,能够量化角速率噪声对系统特性影响的人将拥有明显的优势。他们将能确定性能目标,在应用中产生可观测的值;当其他项目目标 支持考虑特定MEMS陀螺仪时,他们将能有效地量化其对系统的影响后果。一旦有了这种基本理解,系统设计师便可专 注于确定能够满足性能要求的MEMS陀螺仪,利用带宽、速率噪声密度或角向随机游动来指导其考虑。当他们期望优化 所选传感器的噪声性能时,可以利用其与带宽(角速率噪声)和积分时间(角误差)的关系来推动界定其他重要的系 统级特性,从而支持对应用最合适的性能。
关于作者
Mark Looney是ADI公司(美国北卡罗来纳州格林斯博罗)的MEMS和传感器产品线应用工程师。自1998年加入ADI公司以来,他在传感器信号处理、高速模数转换器和DC-DC电源转换领域积累了丰富的工作经验。他拥有内华达州大学雷诺分校电子工程专业学士和硕士学位,曾发表过数篇有关在工业应用中运用MEMS技术的文章。
