1.工程背景与概述

孔边强化工艺在孔表层产生残余压应力，可显著提高含孔构件的疲劳强度，增加构件疲劳寿命。强化的效果主要取决于强化后的残余应力场，其大小和分布对构件抗疲劳性能有着重要的影响。因此，强化时如何合理设置诸工艺参数，产生理想的残余应力场一直是工程技术和研究人员所研究的重点内容。

本课题在王生武教授提出的一种新型孔边模压强化工艺（以下简称模压强化）的基础上，结合前期的实验工作，利用有限元方法对该工艺进行了系统地分析研究，主要包括以下几个方面内容：

（1）利用MSC.MARC软件建立了模压强化工艺过程的有限元模型，采用弹塑性大变形有限元分析方法对其进行了数值仿真。

（2）建立了模压强化的优化数学模型，以iSIGHT软件为平台，孔边周向残余压应力为目标函数，压入量、压模倾角以及摩擦系数等为变量对强化工艺进行优化分析，得到了模压强化的最优设计，从而为模压工具设计及工艺参数设定提供了参考。

2. 优化问题描述

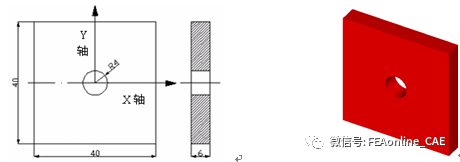
2.1 试样几何图

图2.1为工件几何尺寸图。锥形压模在压力机的作用下，慢慢地压向构件的一边，达到指定位置后保持一段时间以使孔边得到充分地塑性变形,如图2.2（a）所示；然后压模后退，构件上下面翻转1800后对另一面进行模压而形成残余应力场，工艺过程如图2.2（b）、（c）所示。图2.2（d）为模压后的最终状态。

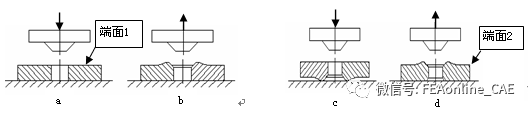
2.2 模压工艺示意图

3. 集成软件的选择

由于模压强化工艺过程集材料、接触与几何非线性为一体，且大的塑性变形可能导致单元发生畸变，导致有限元分析因不收敛而失败。根据模压强化工艺的特点，鉴于MSC.Marc强大的三维网格重划分功能，我们选择MSC.Marc做为有限元数值分析软件进行集成优化。

4. 有限元计算模型介绍

本案例分析对象为无限大板单面模压过程，所以可简化为二维轴对称进行分析。图4.1为完整的系统网格模型，由工件、工作台和压模组成。压模简化为刚体，同时在压模和板之间建立接触单元以传递接触面间的压力，同时也允许接触面之间出现间隙。

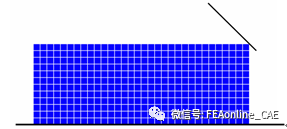
图 4.1模压系统网格

5. 模压强化优化模型 5.1 优化系统结构特点

模压强化问题在优化环节上具有以下特点：

1．模压工艺优化设计问题是非线性优化问题。由于模压强化过程涉及材料、几何和接触非线性问题，使得模压强化的有限元分析呈现出高度的非线性；

2．多峰性，存在多个局部极值点。

5.2 目标函数选择

孔边强化可以显著提高含孔件的疲劳强度和使用寿命，其主要因素是强化引入的残余压应力。残余应力既有平均应力（抵消一部分外载荷）的作用，又有改变裂纹形核地点、抑制裂纹萌生和扩展的作用。根据含孔件疲劳破坏特点，我们把孔边周向残余压应力作为目标函数。

5.3 设计变量的选择

根据模压强化工艺特点，我们选择压模倾角、压入量为作为优化设计变量。

5.4 优化模型

模压强化优化问题可以用以下的非线性规划模型表示：

X 是设计变量，为模压量、压模倾角；

F 是目标函数，为模压后的周向残余应力；

G、H是优化问题必须满足的不等式约束及等式约束，包括几何约束、结构约束等。对于有约束的优化问题，通常需要转化为无约束的优化问题求解，也即把约束作为罚函数加到目标函数上构成增广的目标函数。

5.5 优化算法的选择

根据模压强化的工艺特点，在优化时采用iSIGHT自带遗传算法（GA）和序列二次规划算法的组合优化策略，即先用遗传算法对整个设计空间进行探索，并以此得到全局最优解，在通过逐次二次规划算法对其进行反复迭代和更新来逐步逼近精确的全局最优解。

6. 优化结果及其分析

本文利用了iSIGHT优化平台集成MSC.Marc软件来对模压强化工艺进行优化计算，整个过程共经历了122个循环，优化历程记录如图6.1所示。从图6.1可以看出所对应的目标函数（R）在循环中相对来说变化较大。

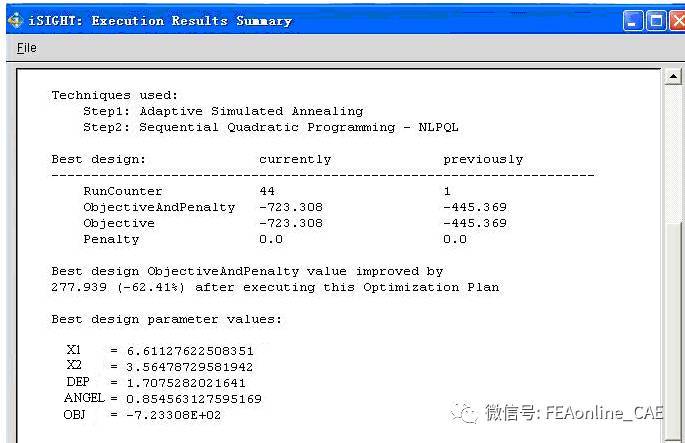
图6.1优化结果图

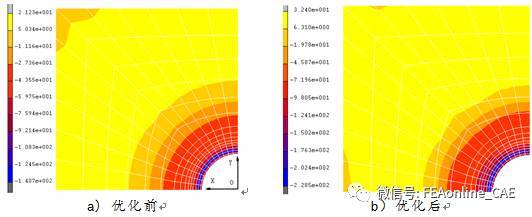
图6.2 优化前、后残余应力分布图

表6.1 优化前后性能参数比较

在孔直径为8的时候，经优化后得到的最优工艺参数为：模压量为1.7，压模倾角为46.80，最大残余应力比设计初始值降低了62.41%。优化前后参数值如表6.1所示。由图6.2可以看出，经过优化后的残余压应力得到较大幅度提高的同时，孔周围的应力梯度也相应地变小，这对工件的疲劳性能提高是有利的。

7. 工程优化点评与提高

本章通过ISIGH集成MSC.MARC软件对模压强化工艺进行了优化。在优化过程中由于压模倾角信息并没有明确体现在输入文件中，本例通过对模型输入文件（*.dat）的分析，通过引入虚拟设计变量建立了几何信息与压模倾角的关系式，从而保证了几何模型正确性，并确保了计算效率。