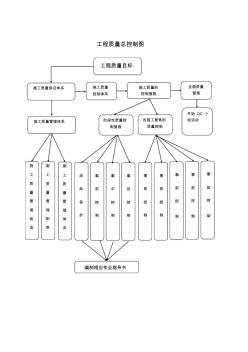
标准差控制图文献

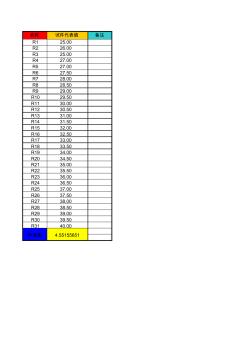 标准差、强度保证率计算公式
标准差、强度保证率计算公式
标准差、强度保证率计算公式
名称 试件代表值 备注 R1 25.00 R2 26.00 R3 25.00 R4 27.00 R5 27.00 R6 27.50 R7 28.00 R8 28.50 R9 29.00 R10 29.50 R11 30.00 R12 30.50 R13 31.00 R14 31.50 R15 32.00 R16 32.50 R17 33.00 R18 33.50 R19 34.00 R20 34.50 R21 35.00 R22 35.50 R23 36.00 R24 36.50 R25 37.00 R26 37.50 R27 38.00 R28 38.50 R29 39.00 R30 39.50 R31 40.00 标准差 4.55155651