点到直线的距离微课制作文献

 点到平面的距离(1)
点到平面的距离(1)
点到平面的距离(1)
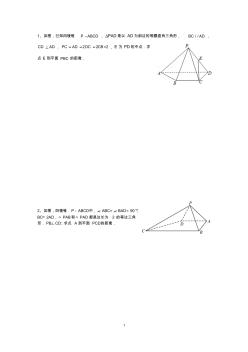
1 1、如图,已知四棱锥 P ABCD , PAD是以 AD为斜边的等腰直角三角形, / /BC AD , CD AD , 2 2 =2PC AD DC CB , E 为 PD的中点.求 点 E 到平面 PBC 的距离 . 2、如图,四棱锥 P-ABCD中,∠ ABC=∠ BAD= 90°, BC= 2AD,△ PAB和△ PAD都是边长为 2 的等边三角 形. PB⊥CD;求点 A到平面 PCD的距离. 2 3 、 如 图 , 在 四 棱 锥 P ABCD 中 , / /C D P A D A BCD平面 , 4 4, ,CD AD AB AC PA且 M 是线段 CP上一点 / / 1 1 = = 4 2 PM PC AP AD P DMB A平求 面且 , 证 , M ABCD并求点 到平面 的距离 4、如图,四棱锥 P ABCD中,底面 ABCD 为平行四边形, 60DAB

 点到平面的距离(文科)
点到平面的距离(文科)
点到平面的距离(文科)
点到平面的距离 (文科数学 ) 1.【2018 年全国卷 II 文】如图,在三棱锥 中, , , 为 的中点. (1)证明: 平面 ; (2)若点 在棱 上,且 ,求点 到平面 的距离. 【答案】(1)见解析( 2) . (2)作 CH⊥OM,垂足为 H.又由( 1)可得 OP⊥CH,所以 CH⊥平面 POM.故 CH的长 F E D C BA 为点 C到平面 POM 的距离.由题设可知 OC= =2,CM = = ,∠ ACB=45°.所以 OM= ,CH= = . 所以点 C到平面 POM 的距离为 . 点睛:立体几何解答题在高考中难度低于解析几何, 属于易得分题, 第一问多以线面的证明 为主,解题的核心是能将问题转化为线线关系的证明; 本题第二问可以通过作出点到平面的 距离线段求解,也可利用等体积法解决 . 2. (2005年福建高考题)如图 1,直二面角 EABD 中,四边形 A
