选择特殊符号
选择搜索类型
请输入搜索

将均匀长线分成许多长度元dχ,其中之一见图1a。对该长度元忽略参数的分布性,可得出其集总参数电路模型(图1b)。将每个长度元都这样处理后,得出的由许多集总参数电路作为环节级联而成的链形电路就是整个均匀长线的电路模型。若设图1a所示长度元的A点和B点距长线的始端的距离分别为χ和χ+dχ;在某一瞬间A点的电压为V,电流为I;在B点的电压为V+dV,电流为I+dI, 则对此长度元的集总参数电路模型(图1b)可用KVL和KCL导出偏微分方程组 通常称为亥维赛电报方程。在正弦稳态下,使用电压和电流的相量可将上述方程组化为
式中Z0称为线阻抗,Y0称为线导纳。 联立式(5)和式(6)求解,可得电压和电流的正弦稳态解
式中A1和A2是需要根据边界条件定出的两个常数,通常都是复数,可分别记为A1=a1e拸$和A2=a2e拹$
行波、入射波和反射波 长线的一个明显的特征是其电压和电流正弦稳态解中的两个分量的波形皆随时间的变化而沿线移动。这种沿线向一个方向移动的波称为行波。将式(7)和式(8)改写成瞬时值形式
便容易证实这一点。电压表达式右端第一项代表的电压分量VI(χ ,t) 是以速度(称为相速或波速)
沿线向χ 增加方向传播的行波,而且随着波的前进,振幅按因子 e-βχ决定的指数律衰减。这个从始端向终端传播的行波称为电压入射波。图2a表示出 t=t0和t=t0+Δt时的VI(χ ,t)曲线。同样,电流分量IφI(χ ,t)也是一个行波,称为电流入射波。电压(电流)的另一个分量VR(χ,t)·【IR(χ,t)】也是 一个行波,波速也是vp。但由于相位中与χ 有关的项是αχ,而不是-αχ,所以这个波的传播方向与VφI(χ ,t)【IφI(χ ,t)】的传播方向相反。另外,由于因子eβχ随χ的减少而减少,其振幅也随着波的前进而逐渐衰减。这个从终端向始端传播的行波称为电压(电流)反射波。图2b表示的是电压反射波VR(χ ,t)的波过程。 式(9)和式(10)的 β和α分别称为衰减系数和相位系数。前者决定波振幅衰减的快慢,后者决定波相位变化的快慢。

在电路理论中,对分布参数电路进行分析时,首先是建立模型。建立模型采用的是无限逼近法。这种方法是将分析对象(例如均匀传输线)设想为许多个无穷小长度元dx。由于长度元dx是无穷小量,在这些长度元的范围内参数可以集中。于是,每个长度元可以抽象成一个集总参数电路。而这些集总参数电路级联而成的链形电路就成为整个均匀传输线的电路模型。显然,只有无穷小长度元dx的个数为无限多时,链形电路才能准确地代表均匀传输线。接着是根据模型写方程。方程是参照长度元dx抽象成的集总参数电路,利用KCL和KVL(见基尔霍夫定律)写出的。它是一个偏微分方程组。最后是解方程求解答,再根据解答讨论电路(即传输线)的性能。 如果建模完成后,再用合适的实际电阻器、电感器和电容器来实现,便可得到一个线性尺寸很小的称为人工线的实际链形电路。这就提供了对传输线进行实验研究的条件。人们可以在实验室内利用很短的人工线实现对长达几百公里,甚而上千公里的输电线上的各种工作状态的观察和各种数据的测量。 分布参数电路作为一个电磁系统当然还可采用电磁场理论进行分析。这样做虽然严格与精确,但并不方便,因为求解电磁场方程组要比求解电路方程组困难得多。因此,通常是采用电路理论来分析分布参数电路。 传输线 传送能量或信号的各种传输线的总称。其中包括电力传输线、电信传输线、天线等。传输线又称长线。由于它具有在空间某个方向上其长度已可与其内部电压、电流的波长相比拟,而必须考虑参数分布性的特征,所以是典型的分布参数电路。在电路理论中讨论传输线时以均匀传输线作为对象。均匀传输线是指参数沿线均匀分布的二线传输线,其基本参数,或称原参数是R0、L0、C0和G0。其中R0 代表单位长度线(包括来线与回线)的电阻;L0代表单位长度来线与回线形成的电感;C0和G0分别代表单位长度来线与回线间的电容和漏电导。这些参数是由导线所用的材料、截面的几何形状与尺寸、导线间的距离,以及导线周围介质决定的。在高频和低频高电压下它们都有近似的计算公式。
对分布参数电路的研究始于19世纪中叶。1856年物理学家开尔文针对当时利用海底电缆传送电报出现的信号延迟、畸变和变弱的现象,首先提出了海底电缆的理论,成为研究分布参数电路的先驱。1893年,英国工程师O.亥维赛利用J.C.麦克斯韦的自由空间电磁波理论,对二线传输线(包括同轴传输线)导引的电磁波,首次提出了简明而又普遍化的解释,从而全面地建立了传输线(长线)的经典理论。
简单的说,集总电路即为理想电路,所有元件均为理想元件,如理想运放即为一标准的线性放大器,放大倍数为无穷大而分布参数电路为实际运用中的电路,每一种元件并不是完美的,如电阻还存在电感,晶体管有结电容。导线...
单稳态电路只有一个稳定状态,触发翻转后经过一段时间会回到原来的稳定状态,一般作固定脉冲宽度整形。当输入Vi保持高电平时,Ci相当于断开。输入Vi'由于Ri的存在而为高电平Vcc。此时:①若定时...
首先,要区分触发器和锁存器。锁存器是一种脉冲电平敏感的存储单元。最主要的特点是具有使能性的锁存电平功能,即在使能信号有效时,可以锁住输出信号保持不变,而在使能信号失效时,输出与输入相同,等效于一个输出...
分布参数电路是必须考虑电路元件参数分布性的电路。参数的分布性指电路中同一瞬间相邻两点的电位和电流都不相同。这说明分布参数电路中的电压和电流除了是时间的函数外,还是空间坐标的函数。
用长线终端处的电压妭2和电流夒2作为边界条件定出常数A1和A2后,可得出用妭2和夒2表示的线上任一点处电压和电流,即 式中χ┡是从终端算起的距离。 在长线终端处电压和电流反射波相量分别与电压和电流入射波相量之比称为电压反射系数和电流反射系数,式中ZL=妭2/夒2是负载阻抗。 当终端所接负载阻抗ZL等于特性阻抗时,反射系数等于零,说明在这种情形下不存在反射波。均匀传输线不存在反射波的运行状态称匹配状态,简称匹配。这时的负载称为匹配负载。 因为无反射波将能量携带回始端(电源端)的现象发生,所以由始端送达终端(负载端)的能量将全部被负载吸收。在这种状态下,负载吸收的功率为
式中ZC和θC分别是特性阻抗的模与幅角。这一功率称为自然功率。入端阻抗
即从长线上任何一处向终端看去,入端阻抗均等于特性阻抗。因此,特性阻抗又称重复阻抗。

式中夒娦前的负号表示终端电流的参考方向改选为由终端指向始端。将上述方程与二端口网络的含T 参数的方程比较一下发现,当只关心长线始端或终端的电压或电流时,整个长线可视为一个无源二端口网络,其 T参数为线上各点的电压和电流均随时间t 作正弦变化, 而二者之振幅也随χ┡作正弦变化。
也 就是说,在前一类点上出现电压的波腹,在后一类点上出现电压的波节。从电流的波形图上看到的恰好相反,在各点上出现电流的波节,在各点上出现电流的波腹。由于这些波腹、波节都驻立不动,所以电压、电流波亦驻立不动而成为驻波。此时入端阻抗式中X1为电抗。由此式可知入端阻抗是一纯电抗,并且随线的长度l而异,在时为容抗;在时为感抗,余类推(图4b)。在时,入端阻抗为零,相当于电压谐振;而在时,入端阻抗为无限大,相当电流谐振(图4c)。 无损耗传输线短路时的情况可作类似的讨论,得到的结论与空载时的结论互为对偶。入端阻抗的上述性质使得无损耗传输线在高频电路中获得多方面的应用。例如开路线和短路线都可用作电抗元件,开路线可充当电容器,而的短路线则能充当电感器;又例如可利用长度等于的开路线或短路线作为具有高品质因数的振荡回路。另外,将长为无损耗线接在一般长线与纯电阻负载之间会起一个阻抗变换器的作用,使负载与长线相匹配,等等。


 RLC电路稳态特性研究
RLC电路稳态特性研究
RLC电路稳态特性研究
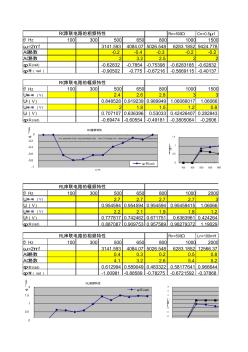
Rn=500Ω Cn=0.5μf f/ Hz 100 300 500 650 800 1000 1500 ω=2π f 3141.593 4084.07 5026.548 6283.1852 9424.778 AB格数 -0.2 -0.4 -0.3 -0.2 -0.2 AC格数 2 3.2 2.5 2 2 φ实 (rad) -0.62832 -0.7854 -0.75398 -0.6283185 -0.62832 φ理( rad) -0.90502 -0.775 -0.67216 -0.5669115 -0.40137 f/ Hz 100 300 500 650 800 1000 1500 UR峰-峰 (V) 2.4 2.6 2.8 3 3 UR(V) 0.848528 0.919239 0.989949 1.06066017 1.06066 Uc峰-峰 (V) 2 1.8 1.5 1.2

 RLC串联电路稳态特性的研究
RLC串联电路稳态特性的研究
RLC串联电路稳态特性的研究
1 学院学生实验报告 成绩: 指导教师: 专业: 班别: 实验时间: 实验人: 学号: 同组实验人: 实验名称: 串联电路稳态特性的研究 实验目的 : 1.观测串联电路的幅频特性和相频特性。 2. 学习用示波器测量位相差 3. 复习交流电路中的矢量图解法 实验仪器:信号发生器,示波器,交流毫伏表,电阻箱,标准电容箱,标准电感,导线若干。 2 f U U U R C R C U R U C 0 L R R U L U U 0 R U L U 实验原理: 1.串联电路的幅频特性和相频特性 (1)串联电路如图 19-1,根据欧姆定律,电路的有效电流为,电路的阻抗为 ,电 阻电压为,电阻电压为,总电压 ,U 落后于 I 的相位。 2.串联电路的幅频特性和相频特性 如图 19-3,据欧姆定律,电路的电流,阻抗为, R 端电压
集中参数模型中模型的各变量与空间位置无关,而把变量看作在整个系统中是均一的,对于稳态模型,其为代数方程,对于动态模型,则为常微分方程。
分布参数模型中至少有一个变量与空间位置有关,所建立的模型对于稳态模型为空间自变量的常微分方程,对于动态模型为空间、时间自变量的偏微分模型 组成电路模型的元件,都是能反映实际电路中元件主要物理特征的理想元件。
由于电路中实际元件在工作过程中和电磁现象有关。
因此有三种最基本的理想电路元件:
表示消耗电能的理想电阻元件R;表示贮存电场能的理想电容元件C;表示贮存磁场能的理想电感元件L,当实际电路的尺寸远小于电路工作时电磁波的波长时,可以把元件的作用集总在一起,用一个或有限个R、L、C元件来加以描述,这样的电路参数叫做集总参数。而集总参数元件则是每一个具有两个端钮的元 件,从一个端钮流入的电流等于从另一个端钮流出的电流;端钮间的电压为单值量。 参数的分布性指电路中同一瞬间相邻两点的电位和电流都不相同。这说明分布参数电路中的电压和电流除了是时间的函数外,还是空间坐标的函数。 一个电路应该作为集总参数电路,还是作为分布参数电路,或者说,要不要考虑参数的分布性,取决于其本身的线性尺寸与表征其内部电磁过程的电 压、电流的波长之间的关系。若用 l表示电路本身的最大线性尺寸,用λ表示电压或电流的波长,则当不等式 λ>>l 成立,电路便可视为集总参数电路,否则便需作为分布参数电路处理。电力系统中,远距离的高压电力传输线即是典型的分布参数电路 ,因50赫兹(Hz)的电流 、电压其波长虽为 6000 千米,但线路长度达几百甚至几千千米,已可与波长相比。通信系统中发射天线等的实际尺寸虽不太长,但发射信号频率高、波长短 ,也应作分布参数电路处理。 研究分布参数电路时,常以具有两条平行导线、而且参数沿线均匀分布的传输线为对象。这种传输线称为均匀传输线(或均匀长线)。作这样的选择是因为实际应用的传输线可以等效转换成具有两条平行导线形式的传输线,而且这种均匀的传输线容易分析。 传输线是传送能量或信号的各种传输线的总称。其中包括电力传输线、电信传输线、天线等。传输线又称长线。由于它具有在空间某个方向上其长度 已可与其内部电压、电流的波长相比拟,而必须考虑参数分布性的特征,所以是典型的分布参数电路。在电路理论中讨论传输线时以均匀传输线作为对象。均匀传输 线是指参数沿线均匀分布的二线传输线,其基本参数,或称原参数是R0、L0、C0和G0。其中R0 代表单位长度线(包括来线与回线)的电阻;L0代表单位长度来线与回线形成的电感;C0和G0分别代表单位长度来线与回线间的电容和漏电导。这些参数是由 导线所用的材料、截面的几何形状与尺寸、导线间的距离,以及导线周围介质决定的。在高频和低频高电压下它们都有近似的计算公式。
传输线可分为长线和短线,长线和短线是相对于波长而言的。所谓长线是指传输线的几何长 度和线上传输电磁波的波长的比值(即电长度)大于或接近于1。反之称为短线。在微波技术中,波长以m 或cm 计,故1m 长度的传输线已长于波长,应视为长线;在电力工程中,即使长度为1000m 的传输线,对于频率为50Hz(即波长为6000km)的交流电来说,仍远小于波长,应视为短线。传输线这个名称均指长线传输线。
长线和短线的区别还在于:前者为分布参数电路,而后者是集中参数电路。在低频电路中常常忽略元件连接线的分布参数效应,认为电场能量全部集中在电容器中,而磁场能量全部集中在电感器中,电阻元件是消耗电磁能量的。由这些集中参数元件组成的电路称为集中参数电路。随着频率的提高,电路元件的辐射损耗,导体损耗和介质损耗增加,电路元件的参 数也随之变化。当频率提高到其波长和电路的几何尺寸可相比拟时,电场能量和磁场能量的分布空间很难分开,而且连接元件的导线的分布参数就不可忽略,这种电路称为分布参数电路。
⑴在原假设为真时,决定放弃原假设,
称为第一类错误,其出现的概率通常记作α;
⑵在原假设不真时,决定接受原假设,
称为第二类错误,其出现的概率通常记作β.
通常只限定犯第一类错误的最大概率α,
不考虑犯第二类错误的概率β.这样的假设
检验又称为显著性检验,
概率α称为显著性水平.
当H0为μ=μ0,假设检验的结果是放弃H0时,
如果α=0.05,则称μ与μ0有显著的差异或
差异显著;如果水平α=0.01,则称μ与μ0有
极显著的差异或差异极显著.
假设检验的步骤如下:
⑴提出H0和H1;
⑵指定概率α;
⑶寻求统计量g(X1,X2,…,Xn)及其分布;
⑸当统计量的观测值g(x1,x2,…,xn)满足
不等式时放弃H0,否则接受H0.
⑷在H0为真时构造小概率事件并推导
g()所满足的不等式;
习惯上称观测值g(x1,x2,…,xn)所
满足的不等式为假设检验方案,称这个不等式所确定的观测值g的取值范围为假设检验的放弃域.
放弃域由两个区间构成的假设检
验被形容为双侧检验,放弃域由一个
区间构成的假设检验被形容为单侧检
验.
H0为相等,H1为不相等的假设检验
为双侧检验,观测值g()较大或较小时
放弃H0;
H0为相等,H1为大于的假设检验为单
侧检验,观测值g()较大时放弃H0;
H0为相等,H1为小于的假设检验为
单侧检验,观测值g()较小时放弃H0.
2.一个正态总体均值或方差的假设检验
为,修正方差的观测值为s*2,离均差
平方和的观测值为ss,显著性水平为α,
则有:
设总体X服从N(μ,σ2)分布,X的一个
样本为X1,X2,…,Xn,均值为,修正
方差为S*2,离均差平方和为SS,样本
的观测值为x1,x2,…,xn,均值的观测值
结论1)若σ2已知,对于给定的数值μ0,
作一个正态总体均值的假设检验时,
H0为μ=μ0,而H1分别为
①μ≠μ0,②μ>μ0,③μμ0,③μ37.72
计算出u=1.818,
例《品种提纯》一个混杂的小麦品种,
其株高的标准差为14cm,经提纯后随机地
抽出10株,它们的株高(单位:cm)为90,
105,101,95,100,100,101,105,93,97,试
检验提纯后的群体是否比原来的群体较为
整齐,α=0.05.
解:提纯后的群体应该比原来的群体
较为整齐,故设
H0为σ2=196,H1为σ2μ2,③μ1μ2,③μ1
常见的交直流电路,谐振电路,滤波器等都是集中参数电路.
一般电路如果不是集中参数电路,都可以归纳为分布参数电路.