选择特殊符号

Ф δ ° × # Ⅱ Ⅲ ½ ¼

选择搜索类型

市场价信息价参考价询价供应商云知资讯文库百科

热门搜索

造价通

请输入搜索

首页 > 百科 > 装饰百科

铰链四边形

铰链四边形(hinge quadrilateral)是一种特殊的四边形，如果四边形的四条边的边长一定，其四个内角不固定，这样的可以变形的四边形称为铰链四边形，铰链四边形显示四边形的不稳定性。

铰链四边形基本信息

中文名铰链四边形
外文名hinge quadrilateral
所属学科数学
所属问题平面几何（四边形）
特点四边形边长一定，四个内角不固定
性质内接于圆的四边形具有最大的面积

铰链四边形相关定理

我们知道，一个三角形在三边长度给定的条件下，这个三角形的形状及它的面积就被惟一地确定下来，但对四边形来讲，情况就大不相同了，当四边长度给定时，可以做出各种各样形状的四边形。譬如，我们取长度分别为a、b、c、d的四根小木条，并用铰链联成一个活动的四边形(图2)，活动这个四边形的顶角。便可得到各种形状的四边形，这些四边形具有不同的面积。那么在这些四边形中，怎么样的四边形具有最大的面积"para" label-module="para"> 下面的定理回答了这个问题（关于定理的证明请参考相应书籍）。 定理1 在四边长度给定的一切四边形中，内接于圆的四边形具有最大的面积。 细心的读者可能会提出这样的问题：难道在边长给定的条件下，适当调整夹角一定能使四边形内接于圆吗"para" label-module="para"> 引理在保持四边形各边长度的条件下，适当调整它的顶角，一定能够使它内接于圆。

铰链四边形造价信息

市场价
信息价
询价

铰链

规格型号：
MJ20030500，70系列平开门
价格行情：
材料单位：
只
材料品牌：
材料税率：
13%
供应商：
德州国强五金制品有限公司南宁办事处
报价时间：
2022-12-08

查看价格

盖板铰链组件

规格型号：
K-1113826-PG
价格行情：
材料单位：
个
材料品牌：
材料税率：
13%
供应商：
科勒(中国)投资有限公司
报价时间：
2022-12-08

查看价格

盖板铰链组件

规格型号：
K-1113826-BG
价格行情：
材料单位：
个
材料品牌：
材料税率：
13%
供应商：
科勒(中国)投资有限公司
报价时间：
2022-12-08

查看价格

防火铰链

规格型号：
品种:防火铰链,材质:钢,系列:防火门配件
价格行情：
材料单位：
付
材料品牌：
华耀消防
材料税率：
13%
供应商：
安徽华耀消防安全科技有限公司
报价时间：
2022-12-08

查看价格

隐形铰链(下)

规格型号：
YC001-02
价格行情：
材料单位：
支
材料品牌：
材料税率：
13%
供应商：
广东雄进金属制品有限公司(东莞市厂商期刊)
报价时间：
2022-12-08

查看价格

铰链

规格型号：
价格行情：
材料单位：
副
材料税率：
地区时间：
惠州市2003年4季度信息价
所属行业：
建筑工程
备注说明：

查看价格

铰链

规格型号：
价格行情：
材料单位：
副
材料税率：
地区时间：
肇庆市2003年3季度信息价
所属行业：
建筑工程
备注说明：

查看价格

铰链

规格型号：
价格行情：
材料单位：
副
材料税率：
地区时间：
惠州市2005年1季度信息价
所属行业：
建筑工程
备注说明：

查看价格

铰链

规格型号：
价格行情：
材料单位：
副
材料税率：
地区时间：
惠州市2004年4季度信息价
所属行业：
建筑工程
备注说明：

查看价格

铰链

规格型号：
价格行情：
材料单位：
副
材料税率：
地区时间：
肇庆市2003年3季度信息价
所属行业：
建筑工程
备注说明：

查看价格

四边形嵌草砖

规格型号：
50mm厚
需求量：
1m²
报价数：
1
材料品牌：
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2019-05-07

查看价格

单绞四边形格栅网

规格型号：
50×50网孔
需求量：
10300m²
报价数：
2
材料品牌：
材料档次：
普通
费用说明：
不含税费 | 不含运费
询价时间：
2017-07-28

查看价格

四边形马赛克

规格型号：
6mm厚
需求量：
215.23m²
报价数：
1
材料品牌：
东鹏、蒙娜丽莎、冠珠、新中源、能强、马可波罗、萨米特、樵东
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2021-05-10

查看价格

标志牌(四边形)

规格型号：
800×800×2(第Ⅳ类反光膜)
需求量：
1m²
报价数：
1
材料品牌：
材料档次：
中高档
费用说明：
不含税费 | 不含运费
询价时间：
2018-10-17

查看价格

幕墙平行四边形平推窗

规格型号：
请看原档图纸
需求量：
800.0套
报价数：
1
材料品牌：
英国固力
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2016-04-08

查看价格

铰链四边形铰链四边形的面积

当四边长度给定时，四边形面积的最大值 这也就是四边给定且又内接于圆的一般四边形的面积公式。 设a b c d=2p，公式(1)能改写成更对称更完整且便于记忆的形式 或 这个关于a、b、c、d具有对称形式的公式还告诉我们:面枳的最大值与给定边的次序无关，仅由给定的边长a、b、c、d惟一确定。 假如四辺形ABCD的边长中有一边的长度逐渐缩短而最后趋于零，譬如DA=d=0，此吋，四边形退化为三角形，任何三角形都内接于圆，故得三角形面积 这就是著名的海伦公式。因此，上述公式是海伦公式的推广。 公式(1)： 是我国南宋数学家秦九韶在他所著《数书九章》中的三斜求积(已知三边求三角形的面积)公 的推广。2100433B

铰链四边形基本概念

如果四边形的四条边的边长一定，其四个内角不固定，这样的四边形就叫做铰链四边形，铰链四边形的任三边长度之和大于第四边，铰链四边形还有一个重要的性质：在四边长度给定的一切四边形中，内接于圆的四边形具有最大的面积。

铰链四边形常见问题

四边形面积

四边形面积必须要知道角度。
已知四边形边长和两对边角度求四边形

采用正玄定理和余弦定理A/sina=B/sinb=c/sinc和A平方=B平方+C平方-2BC*coma
长方形正方形平行四边形都是四边形对吗？

对。四边形分为一般四边形和特殊四边形两大类：一般四边形就是边和角没有特殊关系的四边形；特殊四边形就是边和角有特殊关系的四边形，包括平行四边形、矩形、菱形、正方形、梯形。

铰链四边形文献

平行四边形设计

平行四边形设计

平行四边形设计

格式：pdf

大小：15KB

页数： 3页

平行四边形设计及反思教学内容：教材第 97—99页例 1、例 2，课堂活动，练习二十第 1—3题。课时目标： 1．能够从图中全面感知平行四边形现象，体会平行四边形在生活情景中的存在。 2．通过观察、操作等活动，认识平行四边形的一些特征。 3．经历探索平行四边形的过程，了解它的基本特征，进一步发展空间观念。教学重点：通过观察、操作等活动，认识平行四边形的一些特征。教学难点：经历探索平行四边形的过程，了解它的基本特征。教学用具：课件，展台板书设计平行四边形两组对边分别平行的四边形＿平行四边形特性：易变形特征：两组对边分别相等两组对角分别相等四个内角的和是 360o 教学流程一．引入 1、揭示课题同学们，我们知道由 3条线段围成的图形叫做三角形，那老师给 4条线段你有可能围成什么图形？（四边形、长方形、正方形、梯形、棱形平行四边形）生活中哪些

在线阅读立即下载

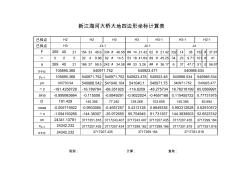大地四边形平差计算表

大地四边形平差计算表

大地四边形平差计算表

格式：pdf

大小：15KB

页数： 1页

已知点已知点 F 269 40 21 154 33 48.6 334 # 48.58 ## 14 21.42 62 # 21.42 332 14 38 152 # 37.97 △ 0 0 0 32 4 9.96 92 # 14.5 53 18 41.84 89 # 45.25 34 23 9.71 101 # 41 a 269 40 21 186 37 58.5 242 # 34.08 ## 33 3.26 ## # 36.17 6 37 47.7 51 0 56.97 y平均 yn+1 yn △y sina D cosa △x xn xn+1 x平均观测：计算：复核： 3717207.435 540923.477 3717299.164 540988.534 -35.972655 55.754949 91.731357 3717207.435 0.4313128 3717243.

在线阅读立即下载

相关推荐

相关百科
相关知识
相关专栏

免费服务热线: 400-888-9639